初中数学人教版七年级上册4.1 几何图形综合与测试综合训练题

这是一份初中数学人教版七年级上册4.1 几何图形综合与测试综合训练题，共15页。试卷主要包含了0分），【答案】D，【答案】C等内容，欢迎下载使用。

一、选择题（本大题共10小题，共30.0分）
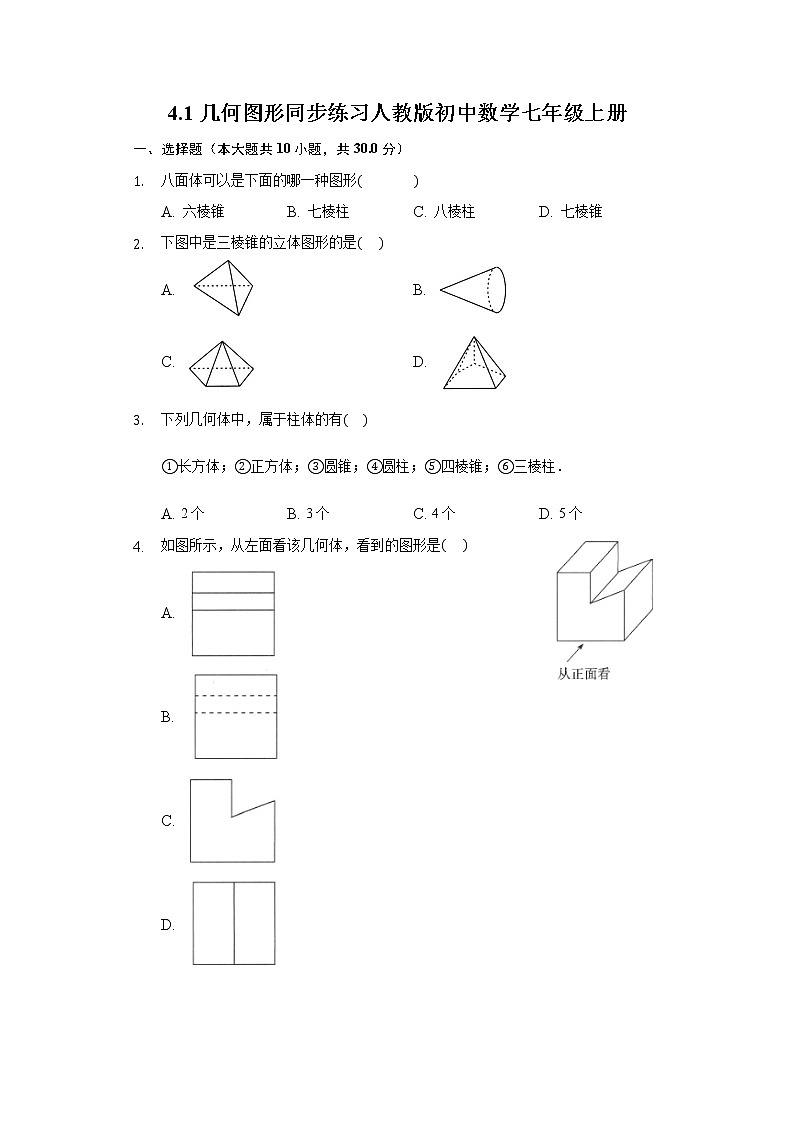
八面体可以是下面的哪一种图形( )
A. 六棱锥B. 七棱柱C. 八棱柱D. 七棱锥
下图中是三棱锥的立体图形的是( )
A. B.
C. D.
下列几何体中，属于柱体的有( )
①长方体；②正方体；③圆锥；④圆柱；⑤四棱锥；⑥三棱柱．
A. 2个B. 3个C. 4个D. 5个
如图所示，从左面看该几何体，看到的图形是( )
A.
B.
C.
D.
如图是一个小正方体的展开图，把展开图折叠成小正方体后，有“新”字一面的相对面上的字是( )
A. 代
B. 中
C. 国
D. 梦
如图四个图形都是由6个大小相同的正方形组成，其中是正方体展开图的是( )
A. ①②③B. ②③④C. ①③④D. ①②④
不透明袋子中装有一个几何体模型，两位同学摸该模型并描述它的特征.甲同学：它有4个面是三角形;乙同学：它有8条棱.该模型的形状对应的立体图形可能是( )
A. 三棱柱B. 四棱柱C. 三棱锥D. 四棱锥
棱长分别是3、5、8的三个正方体被用各种方式粘合在一起形成一个立体图形，在这些立体图形中，表面积最小的那个立体图形的表面积是( )
A. 570B. 502C. 530D. 538
将棱长为4的正方体的表面涂色后，再将其分割成棱长为1的小正方体，其中至多一面涂色的小正方体的个数为( )
A. 48B. 40C. 32D. 28
将一个棱长为m(m>2且m为正整数)的正方体木块的表面染上红色，然后切成m3个棱长为1的小正方体，发现恰有两个表面染有红色的小正方体的数量是有三个表面染有红色的小正方体的数量是的6倍，则m等于( )
A. 4B. 6C. 8D. 10
二、填空题（本大题共4小题，共12.0分）
航天飞机拖着“长长的火焰”，我们用数学知识可解释为点动成线．用数学知识解释下列现象：
(1)一只小蚂蚁爬行留下的路线可解释为________；
(2)电动车车辐条运动形成的图形可解释为________；
(3)薄薄的硬币在桌面上转动时，看上去像球体可解释为________．
小华在一个正方体的六个面上分别写上“x，y，z，1，−1，2”的字样，表面展开图如图所示，若在该正方体中，相对面上的数字相等，则xy= ．
如图是一个长为3cm，宽为2cm的长方形纸片，若将长方形纸片绕长边所在直线旋转一周，得到的几何体的体积为______cm3.(结果保留π)
如图是一个正方体纸盒的表面展开图，若纸盒中相对两个面上的数互为倒数，则代数式a−bc的值为 ．
三、计算题（本大题共3小题，共18.0分）
已知有一个长为5cm，宽为3cm的长方形，若以这个长方形的一边所在的直线为轴，将它旋转一周，请分别求出所得的几何体的表面积和体积．
如图是一个长方体纸盒的平面展开图，已知纸盒中相对两个面上的数互为相反数．
(1)填空：a=_____，b=_____，c=_____．
(2)先化简，再求值：−a2b+2(3ab2−a2b)−3(2ab2−a2b)+abc．
已知一个无盖的长方体容器，它的长宽高之比为2：3：4，且棱长总和为36cm.求这个长方体容器外表面积的最大值．
四、解答题（本大题共3小题，共24.0分）
如图，有27个小方块堆成一个正方体，如果将它的表面涂成黄色．
(1)有3个面涂成黄色的小方块有几块？
(2)有1个面涂成黄色的小方块有几块？
(3)有2个面涂成黄色的小方块有几块？
每个正方体相对两个面上写的数之和等于2．
(1)求图1的正方体看不见的三个面上的数字的积．
(2)现将两个这样的正方体黏合放置(如图2)，求所有看不见的七个面上所写的数的和．
如图，上面是一些具体的物体，下面是一些立体图形，试找出与下面立体图形类似的实物(用线连接)．
答案和解析
1.【答案】D
【解析】
【分析】
本题主要考查平面图形和立体图形.根据棱柱和棱锥的特征解答即可．
【解答】
解：A.六棱锥，有七个面；不符合题意；
B.七棱柱，七个侧面，二个底面，不符合题意；
C.八棱柱 ，八个侧面，二个底面，不符合题意；
D.七棱锥，七个侧面，一个底面，符合题意．
故选D．
2.【答案】A
【解析】
【分析】
本题考查了认识立体图形，主要是对棱锥的定义的考查，熟记概念是解题的关键. 根据常见立体图形对各选项分析判断后利用排除法求解
【解答】
解：A.是三棱锥，故本选项正确；
B.是圆锥，故本选项错误；
C.是四棱锥，故本选项错误；
D.是五棱锥，故本选项错误．
故选A．
3.【答案】C
【解析】
【分析】
此题考查了认识立体图形，熟练掌握柱体的定义是解本题的关键. 找出几何体中属于柱体的即可．
【解答】
解：①长方体；②正方体；③圆锥；④圆柱；⑤四棱锥；⑥三棱柱．这些几何体中，属于柱体的有①②④⑥
故选C．
4.【答案】B
【解析】从左边看是一个长方形，中间有两条水平的虚线，故选B．
5.【答案】D
【解析】解：时与中是对面，代与国是对面，新与梦是对面。
故选：D。
依据正方体的展开图中跳过一个面是它的对面进行判断即可。
本题主要考查的是正方体对面的特点，掌握相关特点是解题的关键。
6.【答案】D
【解析】
【分析】
本题考查了立方体的展开图，由立方体四个侧面和上下两个底面的特征可知，①②④可以拼成一个正方体，而③，上底面不可能有两个，故不是正方体的展开图．由平面图形的折叠及正方体的展开图解题．解题时勿忘记立方体的特征及立方体展开图的各种情形．
【解答】
解：由立方体四个侧面和上下两个底面的特征可知，①②④可以拼成一个正方体，而③，上底面不可能有两个，所以
A.①②③此选项错误；
B.②③④此选项错误；
C.②③④此选项错误；
D.①②④此选项正确．
故选D．
7.【答案】D
【解析】解：四棱锥的底面是四边形，侧面是四个三角形，
底面有四条棱，侧面有4条棱，符合题意，
故选D.
8.【答案】B
【解析】解：将棱长分别为3、5、8的三个正方体粘合在一起形成的立体图形中，减少的表面积最多的是边长分别是3、5的正方形尽可能粘合在一起的面积．
如图所示：
所以，最小的表面积为：
(3×3+5×5+8×8)×6−(3×3)×4−(5×5)×2=98×6−9×4−25×2=502.
故选B.
本题考查了几何体的表面积，注意边长分别是3、5、8的三个正方体被粘合在一起，粘合在一起的立体中，减少的表面积最少的是边长分别是3、5的正方形的面积．先求出边长分别是3、5、8的三个正方体的表面积的和，再减去边长是3、5的两个正方形的面积和的两倍，再减去边长为3的正方形的面积的2倍，即为所求．
9.【答案】C
【解析】
【分析】
此题主要考查了长方体的组合与分割．要熟悉正方体的特点，在分割时有必要可动手操作．根据题意可发现顶点处的小方块三面涂色，除顶点外位于棱上的小方块两面，涂色位于表面中心的一面涂色，而处于正中心的则没涂色，据此解答即可．
【解答】
解：4÷1=4(个)
4×4×4=64(个)
即可以切成64块小正方体．
8×1=8(块)
三个面涂成红色的小正方体有8个．
每条棱上有2个小正方体，12×2=24(块)，
两个面涂成红色的小正方体有24块．
每个面有4个小正方体，(4−2)×(4−2)×6
=2×2×6
=24(块)
一个面涂成红色的小正方体有24块．
没有涂色的小正方体有：64−8−24−24=8(块)，
∴至多一面涂色的小正方体的个数为：24+8=32(块)．
故选C．
10.【答案】B
【解析】
【分析】
本题主要考查了正方体，解决问题的关键是抓住表面涂色的正方体切割小正方体的特点：1面涂色的在面上，2面涂色的在棱长上，3面涂色的在顶点处，没有涂色的在内部，由此即可解决此类问题．恰有两个表面染有红色的小正方体的数量12(m−2)，有三个表面染有红色的小正方体的数量为8，根据恰有两个表面染有红色的小正方体的数量是恰有三个表面染有红色的小正方体的数量的6倍，即可得到m的值．
【解答】
解：将一个棱长为m(m>2且m为正整数)的正方体木块的表面染上红色，然后切成m3个棱长为1的小正方体，则
有三个表面染有红色的小正方体的数量为8，
恰有两个表面染有红色的小正方体的数量12(m−2)，
∵恰有两个表面染有红色的小正方体的数量是有三个表面染有红色的小正方体的数量的6倍，
∴12(m−2)=6×8，
解得m=6，
故选：B．
11.【答案】(1)点动成线；
(2)线动成面；
(3)面动成体．
【解析】
【分析】
本题主要考查的是点、线、面、体的认识的有关知识.根据从运动的观点来看点动成线，线动成面，面动成体解答即可．
【解答】
解：(1)一只蚂蚁爬行留下的路程可解释为点动成线，
故答案为点动成线；
(2)电动车车辐条运动形成的图形可解释为线动成面，
故答案为线动成面；
(3)薄薄的硬币在桌面上转动时，看上去像球体可解释为面动成体，
故答案为面动成体．
12.【答案】1
【解析】 ∵正方体的表面展开图，相对的面之间一定相隔一个正方形，
∴“x”与“−1”在相对面上，
“y”与“2”在相对面上，
“1”与“z”在相对面上，
∵在该正方体中，相对面上的数字相等，
∴x=−1，y=2，
∴xy=(−1)2=1．
13.【答案】12π
【解析】解：将长方形纸片绕长边所在直线旋转一周，得到的几何体是底面半径为2cm，高为3cm的圆柱体，
所以：体积为：π×22×3=12πcm3，
故答案为：12π．
将长方形纸片绕长边所在直线旋转一周，得到的几何体是底面半径为2cm，高为3cm的圆柱体，根据体积计算公式进行计算即可．
考查点、线、面、体之间的关系，关键是旋转后的几何体的各个部分与长方形的长宽之间的关系．
14.【答案】−12021
【解析】根据题意，
得a=−2，b=17，c=−13，
所以a−bc=−2−17×−13=−12021
15.【答案】解：(1)以长为5cm的边为轴旋转一周：表面积：π×32×2+2π×3×5=48πcm2，；体积：π×32×5=45πcm3，
(2)以宽为3cm的边为轴旋转一周：表面积：π×52×2+2π×5×3=80πcm2，；体积：π×52×3=75πcm3，
答：所得的几何体的表面积和体积为48πcm2，45πcm3或80πcm2，75πcm3，
【解析】以不同的边为轴旋转一周，可以得到底面半径为3cm，高为5cm，或者得到底面半径为5cm，高为3cm的圆柱体，分别求出结果即可．
考查圆柱体的展开图，以及面动成体的数学思想，根据不同的轴旋转得到不同的圆柱体，也是分类思想的应用．
16.【答案】(1)1，−2，−3．
(2)原式=−a2b+6ab2−2a2b−6ab2+3a2b+abc，
=abc，
当a=1，b=−2，c=−3；
原式=1×(−2)×(−3)=6．
【解析】
【试题解析】
解：(1)由长方体纸盒的平面展开图知，a与−1、b与2、c与3是相对的两个面上的数字或字母，
因为相对的两个面上的数互为相反数，
所以a=1，b=−2，c=−3．
故答案为：1，−2，−3．
(2)见答案．
【分析】
(1)先根据长方体的平面展开图确定a、b、c所对的面的数字，再根据相对的两个面上的数互为相反数，确定a、b、c的值；
(2)化简代数式后代入求值
本题考查了长方体的平面展开图、相反数及代数式的化简求值．解决本题的关键是根据平面展开图确定a、b、c的值．

17.【答案】解：设长方体的长宽高分别为2x厘米，3x厘米，4x厘米，根据题意得，
2x+3x+4x=36÷4，
解得x=1，
所以长方体的长宽高分别为2厘米，3厘米，4厘米，
所以外表面积的最大值是：
2×3+3×4×2+2×4×2=46(平方厘米)．
答：这个长方体容器外表面积的最大值是46平方厘米．
【解析】设长方体的长宽高分别为2x厘米，3x厘米，4x厘米，根据题意列出方程可得x的值，进而可求这个长方体容器外表面积的最大值．
本题考查了几何体的表面积、认识立体图形，解决本题的关键是掌握正方体的表面积公式．
18.【答案】解：(1)三面黄的小正方体在8个顶点上：8块，
即有3个面涂成黄色的小方块有8块．
(2)一面黄色的小正方体在6个面上：(3−2)×(3−2)×6=6块，
即有1个面涂成黄色的小方块有6块．
(3)两面黄色的正方体在12条棱上：(3−2)×12=12块，
即有2个面涂成黄色的小方块有12块．
【解析】本题主要考查了平面图形和立体图形的认识．
(1)根据正方体的性质可知三面黄的小正方体在8个顶点上，
(2)根据正方体的性质可知一面黄色的小正方体在6个面上，
(3)根据正方体的性质可知两面黄色的正方体在12条棱上．
19.【答案】解：(1)∵每个正方体上相对两个面上写的数字之和都等于2，
∴正方体的下底面数字是1，后面的数字是4，左面的数字是−1，
∴它们的积是1×4×(−1)=−4；
(2)∵每个正方体上相对两个面上写的数字之和都等于2，
∴左边的正方体的下底面数字是1，后面的数字是13，左右两面的数字的和是2，
右面的正方体下底面数字是6，左面的数字是−1，后面的数字是0，
∴它们的和是1+13+2+6−1+0=813．
【解析】(1)根据相对面上的数字的和等于2，分别求出看不见的三个数字，然后相乘即可得解；
(2)根据相对面上的数字的和等于2，分别求出看不见的七个数字，然后相加即可得解．
本题考查灵活运用正方体的相对面解答问题，立意新颖，需要注意左边正方体的左右两面都看不见，所以不需要知道具体数字，只要利用它们的和等于2即可．
20.【答案】连线如图所示：

【解析】见答案