数学八年级上册12.2 三角形全等的判定习题

这是一份数学八年级上册12.2 三角形全等的判定习题，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


一、选择题
1．如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么，最省事的方法是（ ）
A．带①去B．带②去
C．带③去D．带①去和带②去
2．如图，要测量河两岸相对的两点A，B的距离，先在的垂线上取两点C，D，使，再作出的垂线，使A，C，E在一条直线上，可以说明，得，因此测得的长就是的长，判定最恰当的理由是（ ）
A．边角边B．角角边C．边边边D．角边角
3．下列判断中错误的是( )
A．有两角和其中一个角的对边对应相等的两个三角形全等
B．有一边相等的两个等边三角形全等
C．有两边和一角对应相等的两个三角形全等
D．有两边和其中一边上的中线对应相等的两个三角形全等
4．如图，AB⊥BF，ED⊥BF，CD＝CB，判定△EDC≌△ABC的理由是（ ）
A．ASAB．SASC．SSSD．HL
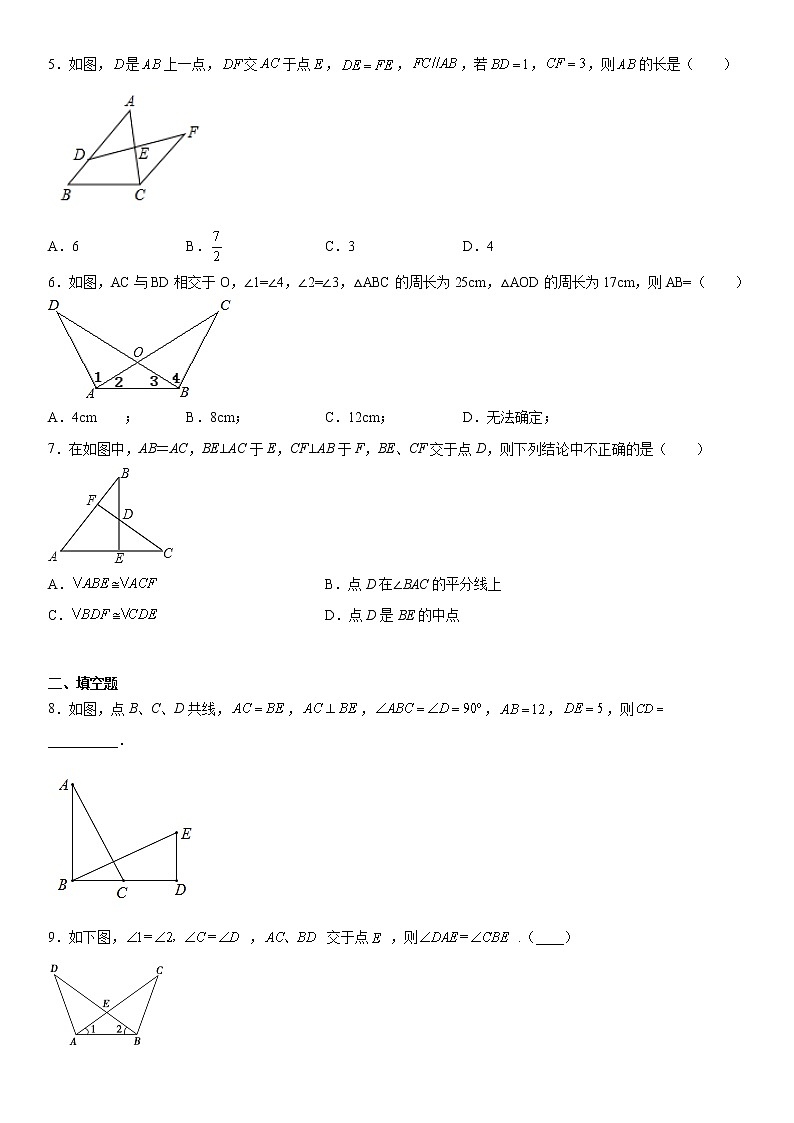
5．如图，是上一点，交于点，，，若，，则的长是（ ）
A．6B．C．3D．4
6．如图，AC与BD相交于O，∠1=∠4，∠2=∠3，△ABC的周长为25cm，△AOD的周长为17cm，则AB=（ ）
A．4cm ；B．8cm；C．12cm；D．无法确定；
7．在如图中，AB＝AC，BE⊥AC于E，CF⊥AB于F，BE、CF交于点D，则下列结论中不正确的是（ ）
A．B．点D在∠BAC的平分线上
C．D．点D是BE的中点
二、填空题
8．如图，点B、C、D共线，，，，，，则__________．
9．如下图， ， 交于点 ，则 .（____）
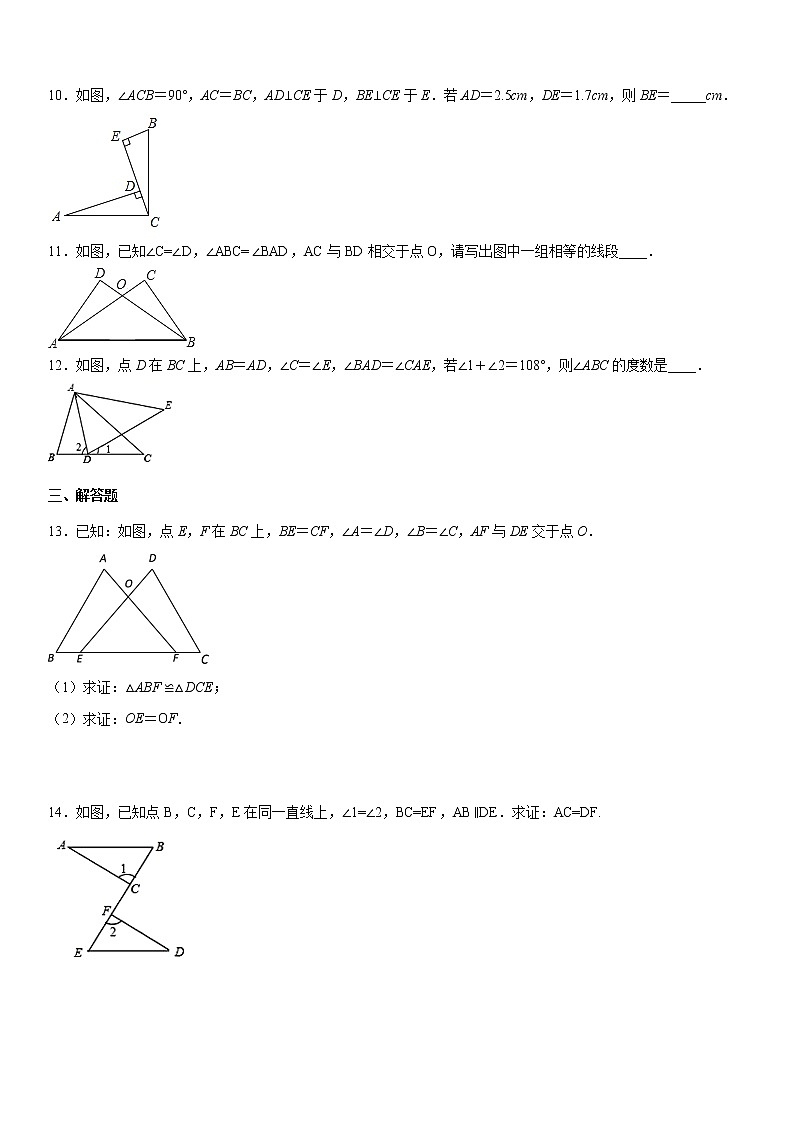
10．如图，∠ACB＝90°，AC＝BC，AD⊥CE于D，BE⊥CE于E．若AD＝2.5cm，DE＝1.7cm，则BE＝_____cm．
11．如图，已知∠C=∠D，∠ABC=∠BAD，AC与BD相交于点O，请写出图中一组相等的线段____．
12．如图，点D在BC上，AB＝AD，∠C＝∠E，∠BAD＝∠CAE，若∠1＋∠2＝108°，则∠ABC的度数是____．
三、解答题
13．已知：如图，点E，F在BC上，BE＝CF，∠A＝∠D，∠B＝∠C，AF与DE交于点O．
（1）求证：△ABF ≌△DCE；
（2）求证：OE＝OF．
14．如图，已知点B，C，F，E在同一直线上，∠1=∠2，BC=EF，AB∥DE．求证：AC=DF.
15．如图，点D在AB上，点E在AC上，AB=AC，∠B=∠C．
（1）求证：BD=CE；
（2）若∠ADC＝90°，试添加一个条件，并求出∠A的度数．
16．如图，点B、F、C、E在直线上（F、C之间不能直接测量），点A、D在异侧，AB∥DE，测得AB=DE，∠A=∠D．
（1）求证：；
（2）若BE=10m，BF=3m，求FC的长度．
17．如图，于点于点， 求证：．
参考答案
1．A
【分析】
已知三角形破损部分的边角，得到原来三角形的边角，根据三角形全等的判定方法，即可求解．
【详解】
解：第①块不仅保留了原来三角形的两个角还保留了一边，则可以根据ASA来配一块一样的玻璃．
故选：A．
【点睛】
此题主要考查了全等三角形的判定方法的开放性的题，要求学生将所学的知识运用于实际生活中，要认真观察图形，根据已知选择方法．
2．D
【分析】
根据全等三角形的判定定理判断即可．
【详解】
证明：∵，，
∴∠ABC=∠EDC=90°，
在和中，
，
∴（角边角），
故选：D．
【点睛】
本题考查了全等三角形的判定，解题关键是根据已知条件判断用了哪个判定定理，两角一边时注意边的位置．
3．C
【详解】
试题分析：对于三角形全等的判定，已知两边和一角的情况，这个角必须是两边的夹角.
考点：三角形全等的判定.
4．A
【分析】
根据垂直定义和对顶角相等，利用全等三角形的判定即可做出判断．
【详解】
∵AB⊥BF，ED⊥BF，
∴∠EDC=∠ABC=90°,
在△EDC和△ABC中，
∴△EDC≌△ABC（ASA）,
故选：A．
【点睛】
本题考查了全等三角形的判定、垂直定义、对顶角相等，熟练掌握全等三角形的判定方法是解答的关键．
5．D
【分析】
只需要证明△ADE≌△CFE即可得出结论．
【详解】
解：∵FC∥AB，
∴∠A=∠ACF，∠F=∠ADF，
又∵DE=EF，
∴△ADE≌△CFE（AAS），
∴CF=AD=3，
∴AB=AD+BD=4，
故选：D．
【点睛】
本题考查了全等三角形的判定和性质，证明△ADE≌△CFE是本题的关键．
6．B
【详解】
分析：先求出∠ABC=∠BAD，然后利用角边角证明△ABC与△BAD全等，根据全等三角形的周长相等可得△ABD的周长为25cm，再根据等角对等边的性质得到AO=BO，求出△AOD的周长等于AD+BD，然后代入数据进行计算即可求出AB的长度．
详解：∵∠1=∠4，∠2=∠3，
∴∠1+∠2=∠3+∠4，
即∠ABC=∠BAD.
在△ABC与△BAD中，
∵∠2＝∠3 ，
AB＝BA ，
∠ABC＝∠BAD，
∴△ABC≌△BAD（ASA），
∵△ABC的周长为25cm，
∴△BAD的周长为25cm，
∵∠2=∠3，
∴AO=BO，
∴△AOD的周长=AD+AO+OD=AD+BO+OD=AB+BD=17cm，
∴AB=△ABD的周长-AD-BD=25-17=8cm．
故选B.
点睛：本题主要考查了全等三角形的判定，等要三角形的判定，求出△AOD的周长等于线段AB与BD的和是解题的关键．
7．D
【分析】
先根据垂直的定义可得，再根据三角形全等的判定定理可得，由此可判断选项A；先根据三角形全等的性质可得，从而可得，再根据三角形全等的判定定理可得，由此可判断选项C；先根据三角形全等的性质可得，再根据角平分线的判定定理即可得判断选项B；先根据三角形全等的性质可得，再根据直角三角形的性质可得，从而可得，由此可判断选项D．
【详解】
，
，
在和中，，
，则选项A正确；
，
，即，
在和中，，
，则选项C正确；
，
又，
点D在的平分线上，则选项B正确；
，
，
是的斜边，DE是的直角边，
，
，
即点D不是BE的中点，选项D不正确；
故选：D．
【点睛】
本题考查了三角形全等的判定定理与性质、角平分线的判定定理等知识点，熟练掌握三角形全等的判定定理与性质是解题关键．
8．7
【分析】
根据全等三角形的判定和性质解答即可．
【详解】
解：∵AC⊥BE，∠ABC=∠D=90°，
∴∠A+∠ABE=∠ABE+∠EBD=90°，
∴∠A=∠EBD，
在△ABC与△BDE中
，
∴△ABC≌△BDE（AAS），
∴DE=BC，AB=BD，
∴CD=BD-BC=AB-DE=12-5=7，
故答案为：7.
【点睛】
本题考查了全等三角形的性质和判定，全等三角形的判定有SAS，ASA，AAS，SSS．
9．对
【分析】
根据三角形全等的判定定理可知，所以，再加上已知条件即可得.
【详解】
（全等三角形对应角相等）
又
故答案为“对”.
【点睛】
本题考查了三角形全等的判定定理、以及三角形全等的性质（全等三角形对应角相等）.
10．0.8．
【分析】
先根据定理证得，再由三角形全等的性质可得，再结合已知的求解即可得.
【详解】
由题意得
在和中，
又
故答案为.
【点睛】
本题考查了三角形全等的判定定理和性质，熟练灵活运用判定定理和性质是解题关键.
11．AC=BD（答案不唯一）
【分析】
利用“角角边”证明△ABC和△BAD全等，再根据全等三角形对应边相等解答即可．
【详解】
解：∵在△ABC和△BAD中，，
∴△ABC≌△BAD（AAS），
∴AC=BD，AD=BC．
故答案为AC=BD（答案不唯一）．
【点睛】
本题考查全等三角形的判定与性质．
12．72°
【分析】
由平角的定义求出∠ADE＝72°，由AAS证明△ABC≌△ADE，得出对应角相等即可求出答案．
【详解】
∵∠1＋∠2＝108°，
∴∠ADE＝72°，
∵∠BAD＝∠CAE，
∴∠BAC＝∠DAE，
在△ABC和△ADE中，
∠BAC＝∠DAE，∠C＝∠E，AB＝AD，
∴△ABC≌△ADE（AAS），
∴∠ABC＝∠ADE＝72°．
故答案为：72°．
【点睛】
本题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定方法是解题的关键．
13．（1）见解析；（2）见解析．
【分析】
（1）由线段的和差证明BF＝CE， 再证明△ABF≌△DCE（AAS）；
（2）由全等三角形对应角相等得到∠AFB=∠DEC，再由等角对等边解题．
【详解】
证明：（1）∵BE＝CF，
∴BE＋EF＝CF＋EF，
即BF＝CE，
又∵∠A＝∠D，∠B＝∠C，
∴△ABF≌△DCE（AAS）；
（2）∵△ABF≌△DCE，
∴∠AFB=∠DEC，
∴OE=OF．
【点睛】
本题考查全等三角形的判定与性质、等角对等边等知识，是重要考点，难度较易，掌握相关知识是解题关键．
14．证明见解析
【分析】
首先根据平行线的性质可得∠B=∠E，然后可利用ASA证明△ABC≌△DEF，从而证出结论．
【详解】
证明： ∵AB∥DE，
∴∠B=∠E，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（ASA）
∴AC=DF．
【点睛】
此题主要考查了全等三角形的判定及性质和平行线的性质，关键是掌握判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
15．（1）见解析；（2）添加条件：∠C＝40°，此时∠A＝50°
【分析】
（1）利用ASA证明△ACD≌△ABE，然后得到AD＝AE，进而得到BD＝CE；
（2）在△ACD中添加∠C＝40°，即可利用直角三角形两锐角互余计算∠A．
【详解】
（1）证明：在△ADE和△FCE中，
∴△ACD≌△ABE，
∴AD＝AE．
∴，即BD＝CE．
（2）添加条件：∠C＝40°,
∵∠ADC＝90°，∠C＝40°,
∴∠A＝90°-40°＝50°．
【点睛】
本题主要考查全等三角形的判定和性质，灵活应用边角关系是解题的关键
16．（1）见解析；（2）4m.
【分析】
（1）由平行可得∠ABC=∠DEF，然后用ASA即可判定全等；
（2）由全等可得BC=EF，可推出BF=CE，即可求出FC.
【详解】
（1）证明：∵AB∥DE，
∴∠ABC=∠DEF
在△ABC和△DEF中，
∴△ABC≌△DEF（ASA）
（2）解：∵△ABC≌△DEF
∴BC=EF
∴BF+FC=FC+CE
∴BF=CE=3m
∴FC=10-3-3=4m
故FC的长度为4m.
【点睛】
本题考查全等三角形的判定和性质，较为简单，掌握判定定理和性质即可解决.
17．详见解析
【分析】
由平行线的性质可得，由垂直的定义可得，从而可根据AAS证明，然后根据全等三角形的性质即得，进而可得结论．
【详解】
证明：，
，
，
，
在和中，
，
，
，
．
【点睛】
本题考查了平行线的性质、垂直的定义和全等三角形的判定和性质，属于基本题型，熟练掌握全等三角形的判定和性质是解题关键．