初中数学北师大版八年级上册2 平方根备课ppt课件

这是一份初中数学北师大版八年级上册2 平方根备课ppt课件，共20页。PPT课件主要包含了回顾与思考，你发现了吗，不存在，探求新知，平方根的表达式为，理解概念，议一议，负数没有平方根，开平方，巩固新知等内容，欢迎下载使用。
3.我们已经学习过哪些运算？它们中互为逆运算的是什么？
答：加、减、乘、除、乘方五种运算.加与减互逆；乘与除互逆.
1.什么叫算术平方根？
2.填空: 9的算术平方根 ，17的算术平方根 .
一般地，如果一个正数x的平方等于a,即 x2 =a ,那么这个正数x叫做a的算术平方根. 记为：读作：“根号a”, a叫做被开方数.0的算术平方根是0.即: =0.负数没有算术平方根.
5.填空: （1）3 2 = ， (－3)2= ；（2）0.82= ，(－0.8)2= .6.平方等于9的数有几个？平方等于0.64的数有几个？
4.什么叫乘方？什么叫幂？
求相同因数的积的运算叫做乘方；乘方运算的结果叫做幂.
平方等于9的数有两个；平方等于0.64的数有两个.
( )2 = 9( )2 = ( )2 = 0( )2 =-4
32 = ( ) (-3 )2 = ( ) ( )2= ( ) ( )2 = ( ) 02 = ( )
一般地，如果一个数的平方等于a，那么这个数叫做a 的平方根或二次方根.而把正的平方根叫算术平方根.
例如:(±4)2=16,则+4和-4都是16的平方根; 即16的平方根是±4; +4是16的算术平方根.
一个正数有几个平方根？它们是什么 关系？0的平方根有几个？负数有平方根吗?
一个正数有两个平方根,它们是互为相反数.
一个，0的平方根是0.
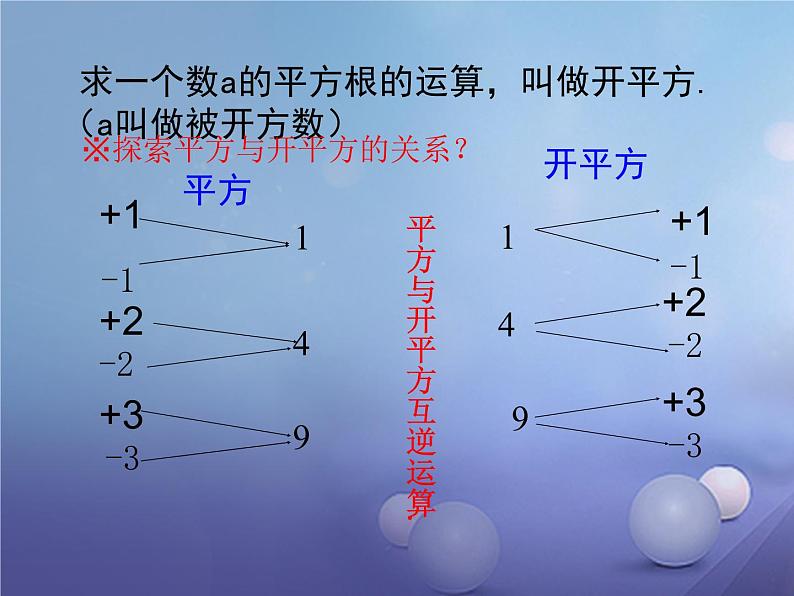
求一个数a的平方根的运算，叫做开平方.（a叫做被开方数）
※探索平方与开平方的关系？
平方与开平方互逆运算.
联系：1.包含关系：平方根包含算术平方根， 算术平方根是平方根的一种.
平方根与算术平方根的联系与区别：
2.只有非负数才有平方根和算术平方根.
3.0的平方根是0，算术平方根也是0.
1.个数不同：一个正数有两个平方根， 但只有一个算术平方根.
例3.求下列各数的平方根:
(3) 0.0004
1.判断下列各数是否有平方根？并说明理由. (1)(－3)2； (2)0； (3)－0.01； (4)－52； (5)－a2 ； (6) a2－2a+22.填空(1)25的平方根是_________； (2)( )2=_________. 3.求下列各数的平方根
运用平方运算求一个非负数的平方根是常用的方法，如被开方数是小数，要注意小数点的位置，也可先将小数化为分数，再求它的平方根，如被开方数是带分数，先要把它化为假分数.
拓广探索：1.已知(a－3)2+｜b－4｜=0，则 的平方根是（ ）
B、±
C、
2.求下列各式中的x.（1）16x2＝81； （2）(x-3)2-25＝0.
正数有2个平方根，0的平方根是0.负数没有平方根.
方法总结：求一个数的平方根就是转化寻找哪个数平方等于这个数. 平方与开方的互化关系.
达标检测，反馈矫正：A组：1.下列各数没有平方根的是（ ）A、0 B、-1 C、10 D、1022. 16的平方根是（ ） A、±4 B、24 C、± D、±23.如果 是 的一个平方根，那么 的算术平方根是（ ） A、 B、 C、 D、 4. 的平方根为_________； ＝ . 5. 求下列各数的平方根： （1）0.01; （2）2
； （3）(－13)2.
B组：（选做）6. (－11)2的平方根是（ ）A、121 B、11 C、±11 D、没有平方根 7.当x≤0时， 的值为（　　）　 A、0 B、 C、 D、 8.一个正数的平方根是2a－1与－a+2， 则a=_________，这个正数是_________.
作业布置：习题2.4 必做题：第1、4题;选做题：第3题.