陕西中考数学基础考点课件+练习题：第21课时 锐角三角函数及其实际应用

这是一份陕西中考数学基础考点课件+练习题：第21课时 锐角三角函数及其实际应用，文件包含陕西中考数学基础考点课件第21课时锐角三角函数及其实际应用pptx、陕西中考数学基础考点练习题第21课时锐角三角函数及其实际应用含答案docx等2份课件配套教学资源，其中PPT共23页， 欢迎下载使用。

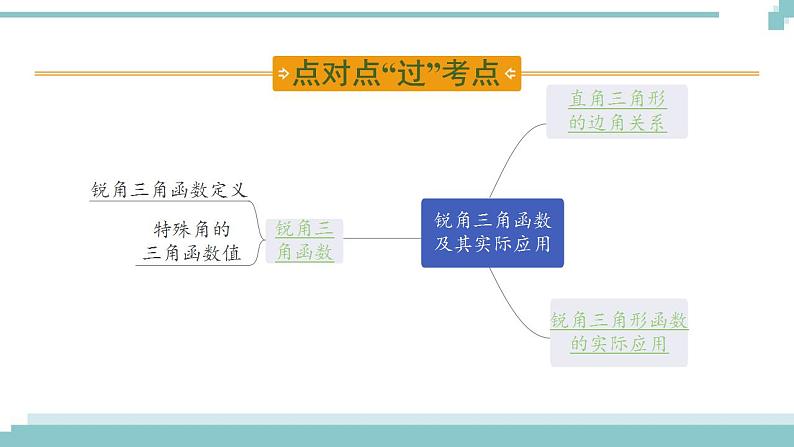
锐角三角函数及其实际应用
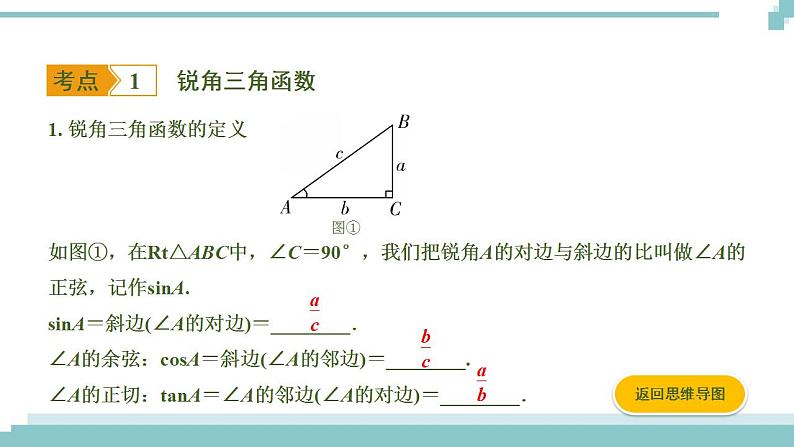
1. 锐角三角函数的定义
如图①，在Rt△ABC中，∠C＝90°，我们把锐角A的对边与斜边的比叫做∠A的正弦，记作sinA.sinA＝斜边(∠A的对边)＝________．∠A的余弦：csA＝斜边(∠A的邻边)＝________.∠A的正切：tanA＝∠A的邻边(∠A的对边)＝________．
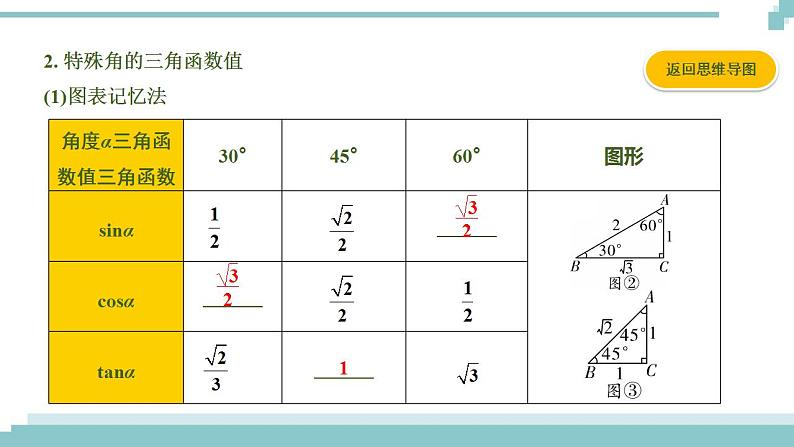
2. 特殊角的三角函数值(1)图表记忆法
(2)规律记忆法：30°、45°、60°角的正弦值的分母都是2，分子依次为1、 、 ；30°、45°、60°角的余弦值恰好是60°、45°、30°角的正弦值．
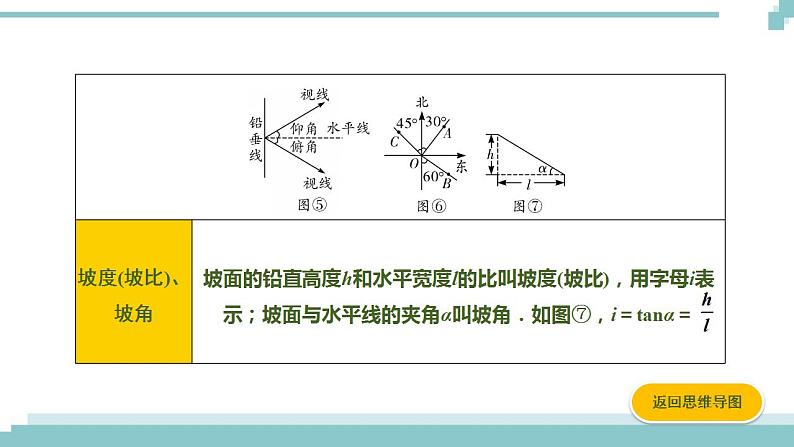
直角三角形的边角关系(如图④)
三边关系：勾股定理： ；三角关系：∠A＋∠B＝∠C＝90°；边角间关系：sinA＝csB＝ ；csA＝sinB＝ ；tanA＝ ，tanB＝ .
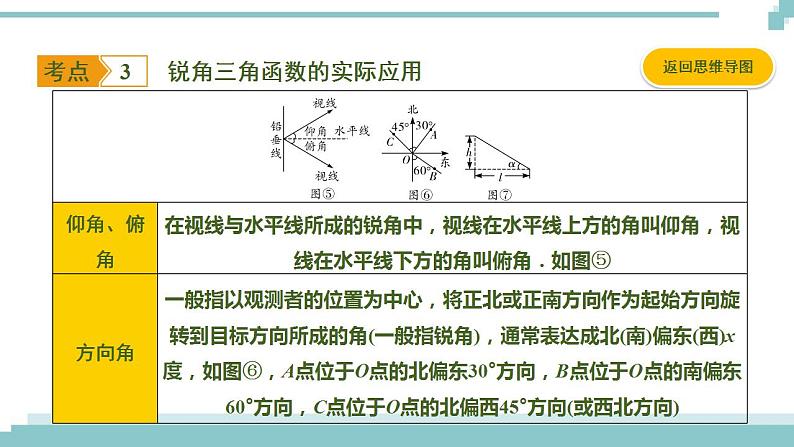
锐角三角函数的实际应用
【模型分析】若三角形中有已知角时，则通过在三角形内作高CD，构造出两个直角三角形求解，其中公共边CD是解题的关键．【等量关系】CD为公共边，AD＋BD＝AB模型演变
【等量关系】如图①，CE＝DA，CD＝EA，CE＋BD＝AB；如图②，CD＝EF，CE＝DF，AD＋CE＋BF＝AB.1. 周六下午，王武和父亲开车出去办事．如图，他们在A处测得其北偏东30°处有一座移动信号发射塔C，当车以每小时60公里的速度向正东方向行驶10分钟到达B处后，此时他们测得信号发射塔C在其北偏西15°处，请你求出此时车和发射塔之间的距离BC.(结果保留根号)
解：如解图，过点B作BD⊥AC于点D，则∠BDA＝∠BDC＝90°，
∠BAC＝90°－30°＝60°，∠ABC＝90°－15°＝75°，
∴∠ABD＝30°，∴∠CBD＝45°，AD＝
∵∠C＝180°－∠BAC－∠ABC＝45°，∴△BCD是等腰直角三角形，
2. 小婷在放学路上，看到隧道上方有一块宣传“垃圾分类从我做起”的竖直标语牌CD.如图，她在A点测得标语牌顶端D处的仰角为42°，测得隧道底端B处的俯角为30°(B，C，D在同一条直线上)，AB＝10 m，隧道高6.5 m(即BC＝6.5 m)，求标语牌CD的高(结果精确到0.1米，参考数据：sin42°≈0.67，cs42°≈0.74，tan42°≈0.90， ≈1.73)
解：如解图，过点A作AE⊥BD于点E.在Rt△AEB中，∵∠EAB＝30°，AB＝10 m，∴BE＝ AB＝5 m，AE＝ m，在Rt△ADE中，DE＝AE·tan42°≈7.79 m，∴BD＝DE＋BE≈12.79 m，∴CD＝BD－BC≈12.79－6.5≈6.3 m，答：标语牌CD的高约为6.3 m.
【模型分析】若三角形中有已知角，通过在三角形外作垂线BC，构造有公共直角的两个三角形求解，其中公共边BC是解题的关键．【等量关系】BC为公共边，如图①，AD＋DC＝AC；如图②，DC－BC＝DB.
【等量关系】如图③，DF＝EC，DE＝FC，BF＋DE＝BC，AE＋DF＝AC；如图④，AF＝CE，AC＝FE，BC＋AF＝BE.模型演变2
【等量关系】如图⑤，BE＋EC＝BC；如图⑥，EC－BC＝BE；如图⑦，AC＝FG，AF＝CG，AD＋DC＝FG，BC＋AF＝BG.
【等量关系】如图⑧，BC＝FG，BF＝CG，AC＋BF＝AG，EF＋BC＝EG；如图⑨，BC＝FG，BF＝CG，EF＋BC＝EG，BD＋DF＝BF，AC＋BD＋DF＝AG.
3. (2019湘潭)我国于2019年6月5日首次完成运载火箭海上发射，这标志着我国火箭发射技术达到了一个崭新的高度．如图，运载火箭从海面发射站点M处垂直海面发射，当火箭到达点A处时，海岸边N处的雷达站测得点N到点A的距离为8千米，仰角为30°.火箭继续直线上升到达点B处，此时海岸边N处的雷达测得B处的仰角增加15°，求此时火箭所在点B处与发射站点M处的距离．(结果精确到0.1千米)(参考数据： ≈1.41， ≈1.73)
解：在Rt△AMN中，cs∠ANM＝ ，∵∠ANM＝30°，AN＝8，∴MN＝AN·cs∠ANM＝8cs30°＝
在Rt△BMN中，∠BNM＝45°，∴MB＝MN＝ ≈4×1.73≈6.9(千米)．答：此时火箭所在点B处与发射站点M处的距离约为6.9千米．
4. (2019陕师大附中模拟)某校在“建设特色校园”的活动中，将本校的办学理念做成宣传牌(AB)，放置在教学楼的顶部(如图所示)．小明在操场上的点D处，用1米高的测角仪CD，从点C处测得宣传牌的底部B的仰角为37°，然后向教学楼正方向走了4米到达点F处，又从点E处测得宣传牌的顶部A的仰角为45°.已知教学楼高BM＝17米，且点A，B，M在同一直线上，求宣传牌AB的高度．(结果精确到0.1米，参考数据： ≈1.73，sin37°≈0.60，cs37°≈0.80，tan37°≈0.75)
解：如解图，过点C作CN⊥BM于点N，则四边形CDMN是矩形，点E在线段CN上．∴BN＝BM－CD＝17－1＝16米，在Rt△BCN中，BN＝16米，∠BEN＝37°，
在Rt△AEN中，∵EN＝CN－CE≈17.33米，∠AEN＝45°，∴AN＝EN·tan45°≈17.33米，∴AB＝AN－BN≈17.33－16≈1.3米．答：宣传牌AB的高度约为1.3米．
【模型分析】分别解两个直角三角形，其中公共边BC是解题的关键．【等量关系】BC为公共边【模型演变】
【等量关系】如图①，BF＋FC＋CE＝BE；如图②，BC＋CE＝BE；如图③，AB＝GE，AG＝BE，BC＋CE＝AG，DG＋AB＝DE.
5. (2019西安铁一中模拟)如图所示，某数学活动小组为了测量小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30°，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是60°，若坡角∠FAE＝30°，求大树的高度．