2022年中考数学专题复习类型六 与圆有关的探究题（原卷版）

类型六 与圆有关的探究题

【典例1】定义：三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角．

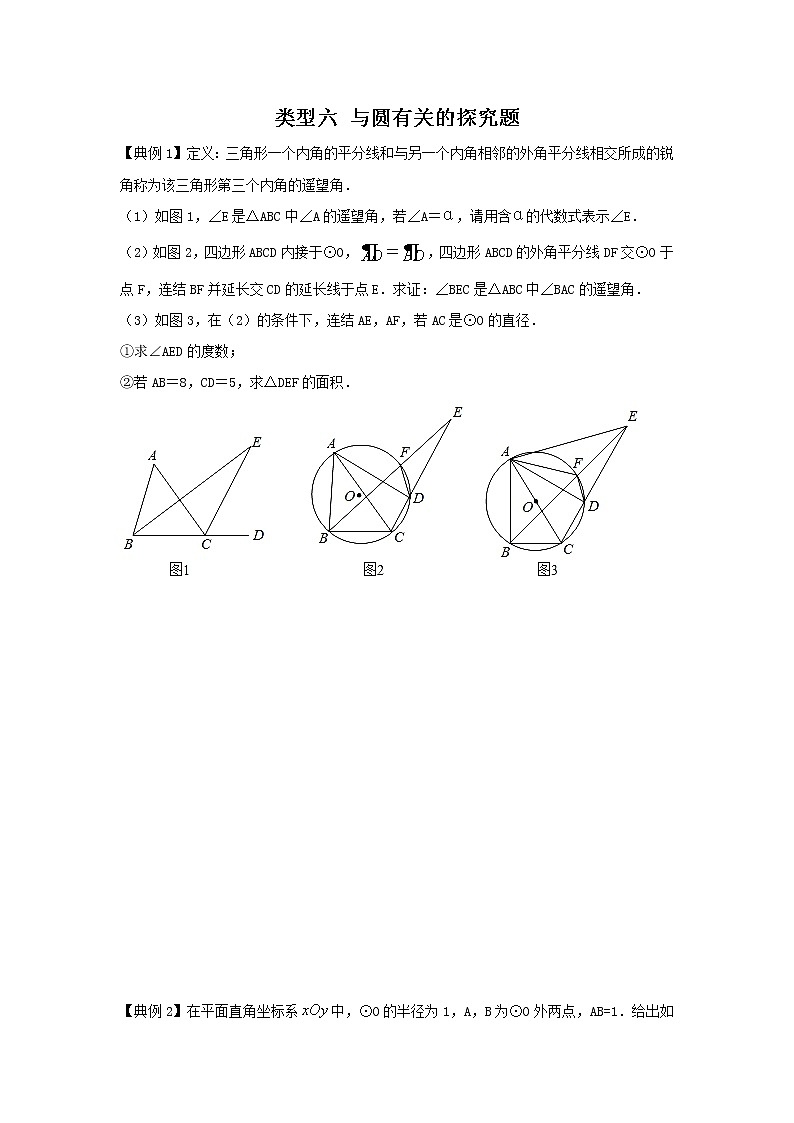
（1）如图1，∠E是△ABC中∠A的遥望角，若∠A＝α，请用含α的代数式表示∠E．

（2）如图2，四边形ABCD内接于⊙O，＝，四边形ABCD的外角平分线DF交⊙O于点F，连结BF并延长交CD的延长线于点E．求证：∠BEC是△ABC中∠BAC的遥望角．

（3）如图3，在（2）的条件下，连结AE，AF，若AC是⊙O的直径．

①求∠AED的度数；

②若AB＝8，CD＝5，求△DEF的面积．

【典例2】在平面直角坐标系中，⊙O的半径为1，A，B为⊙O外两点，AB=1．给出如下定义：平移线段AB，得到⊙O的弦（分别为点A，B的对应点），线段长度的最小值称为线段AB到⊙O的“平移距离”．

（1）如图，平移线段AB到⊙O的长度为1的弦和，则这两条弦的位置关系是           ；在点中，连接点A与点        的线段的长度等于线段AB到⊙O的“平移距离”；

（2）若点A，B都在直线上，记线段AB到⊙O的“平移距离”为，求的最小值；

（3）若点A的坐标为，记线段AB到⊙O的“平移距离”为，直接写出的取值范围．

【典例3】.如图所示,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8.半径为的⊙M与射线BA相切,切点为N,且AN=3.将Rt△ABC顺时针旋转120°后得到Rt△ADE,点B,C的对应点分别是点D,E．

(1)画出旋转后的Rt△ADE；

(2)求出Rt△ADE 的直角边DE被⊙M截得的弦PQ的长度；

(3)判断Rt△ADE的斜边AD所在的直线与⊙M的位置关系,并说明理由.

【典例4】（1）已知：如图1，△ABC是⊙O的内接正三角形，点P为弧BC上一动点，

求证：PA=PB+PC；

（2）如图2，四边形ABCD是⊙O的内接正方形，点P为弧BC上一动点，

求证：；

（3）如图3，六边形ABCDEF是⊙O的内接正六边形，点P为弧BC上一动点，请探究PA、PB、PC三者之间有何数量关系，并给予证明．

【典例5】（1）如图①，M、N分别是⊙O的内接正△ABC的边AB、BC上的点且BM=CN，连接OM、ON，

求∠MON的度数；

（2）图②、③、…④中，M、N分别是⊙O的内接正方形ABCD、正五边ABCDE、…

正n边形ABCDEFG…的边AB、BC上的点，且BM=CN，连接OM、ON，则图②中∠MON的度数是       ，图③中∠MON的度数是       ；…由此可猜测在n边形图中∠MON的度数是           ；

（3）若3≤n≤8，各自有一个正多边形，则从中任取2个图形，恰好都是中心对称图形的概率是             .

【典例6】如图，已知⊙O的直径AB＝2，直线m与⊙ O相切于点A，P为⊙ O上一动点（与点A、点B不重合），PO的延长线与⊙ O相交于点C，过点C的切线与直线m相交于点D．

（1）求证：△APC∽△COD．

（2）设AP＝x，OD＝y，试用含x的代数式表示y．

（3）试探索x为何值时， △ACD是一个等边三角形．

【典例7】 如图①，半圆O的直径AB=6，AM和BN是它的两条切线，CP与半圆O相切于点P，并于AM，BN分别相交于C，D两点．

（1）请直接写出∠COD的度数；

（2）求AC•BD的值；

（3）如图②，连接OP并延长交AM于点Q，连接DQ，试判断△PQD能否与△ACO相似？若能相似，请求AC：BD的值；若不能相似，请说明理由．