人教版八年级上册13.2 画轴对称图形综合与测试达标测试

这是一份人教版八年级上册13.2 画轴对称图形综合与测试达标测试，共16页。试卷主要包含了若点A，若点P，若点M关于y轴对称等内容，欢迎下载使用。

一．选择题（共6小题）
1．坐标平面上有一个轴对称图形，、两点在此图形上且互为对称点．若此图形上有一点C（﹣2，﹣9），则C的对称点坐标为何（ ）
A．（﹣2，1）B．C．D．（8，﹣9）
2．小莹和小博士下棋，小莹执圆子，小博士执方子．如图（﹣1，0）表示，右下角方子的位置用（0，﹣1），所有棋子构成一个轴对称图形．她放的位置是（ ）
A．（﹣2，1）B．（﹣1，1）C．（1，﹣2）D．（﹣1，﹣2）
3．若点A（m，n）和点B（5，﹣7）关于x轴对称（ ）
A．2B．﹣2C．12D．﹣12
4．若点P（a，b）在第二象限，则点Q（a﹣1，﹣b）（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
5．将△ABC的三个顶点的横坐标乘以﹣1，纵坐标不变，则所得图形（ ）
A．与原图形关于y轴对称
B．与原图形关于x轴对称
C．与原图形关于原点对称
D．向x轴的负方向平移了一个单位
6．若点A（1+m，1﹣n）与点B（﹣3，2）关于y轴对称（ ）
A．﹣5B．﹣3C．3D．1
二．填空题（共6小题）
7．已知点A（a，﹣3）与B（，b）关于x轴对称 ．
8．点（2+a，3）关于y轴对称的点的坐标是（﹣4，2﹣b），则ab＝ ．
9．已知点P（1﹣a，a+2）关于y轴的对称点在第二象限，则a的取值范围是 ．
10．若点M（a，﹣1）与点N（2，b）关于y轴对称
11．已知点P（3，a）关于y轴的对称点为Q（b，2），则ab＝ ．
12．点M（3，﹣4）关于x轴的对称点的坐标是 ，关于y轴的对称点的坐标是 ．
三．解答题（共14小题）
13．在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形），C的坐标分别为（﹣4，5），（﹣1，3）．
（1）请在如图所示的网格平面内作出平面直角坐标系；
（2）请作出△ABC关于y轴对称的△A′B′C′；
（3）写出点B′的坐标．
14．如图，在正方形网格上有一个△ABC．
（1）画出△ABC关于直线MN的对称图形（不写画法）；
（2）若网格上的每个小正方形的边长为1，求△ABC的面积．
15．在3×3的正方形格点图中，有格点△ABC和△DEF，且△ABC和△DEF关于某直线成轴对称
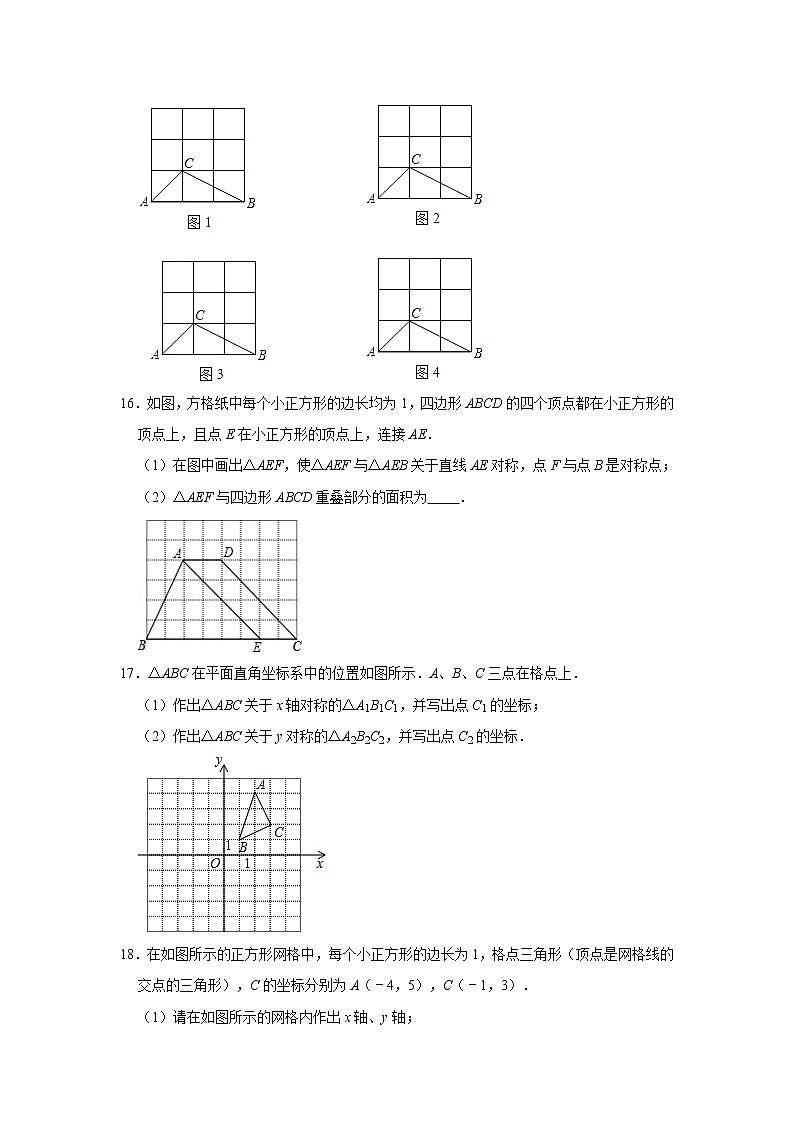
16．如图，方格纸中每个小正方形的边长均为1，四边形ABCD的四个顶点都在小正方形的顶点上，且点E在小正方形的顶点上，连接AE．
（1）在图中画出△AEF，使△AEF与△AEB关于直线AE对称，点F与点B是对称点；
（2）△AEF与四边形ABCD重叠部分的面积为 ．
17．△ABC在平面直角坐标系中的位置如图所示．A、B、C三点在格点上．
（1）作出△ABC关于x轴对称的△A1B1C1，并写出点C1的坐标；
（2）作出△ABC关于y对称的△A2B2C2，并写出点C2的坐标．
18．在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形），C的坐标分别为A（﹣4，5），C（﹣1，3）．
（1）请在如图所示的网格内作出x轴、y轴；
（2）请作出△ABC关于y轴对称的△A1B1C1；
（3）写出点B1的坐标并求出△A1B1C1的面积．
19．在直角坐标系中，△ABC的三个顶点的位置如图所示．
（1）请画出△ABC关于y轴对称的△A′B′C′（其中A′，B′，C′分别是A，B，C的对应点，不写画法）；
（2）直接写出A′，B′，C′三点的坐标：A′（ ），B′（ ），C′（ ）．
20．如图，△ABC和△A′B′C′关于直线MN对称，△A′B′C′和△A″B″C″关于直线EF对称．
（1）画出直线EF；
（2）直线MN与EF相交于点O，试探究∠BOB″与直线MN、EF所夹锐角α的数量关系．
21．如图，方格纸中每个小方格都是边长为1的正方形，我们把以格点连线为边的多边形称为“格点多边形”
（1）求图1中四边形ABCD的面积；
（2）在图2方格纸中画一个格点三角形EFG，使△EFG的面积等于四边形ABCD的面积且为轴对称图形．
22．在直角坐标系中，△ABC的顶点坐标如图所示，
（1）请你在图中先作出△ABC关于直线m（直线m上点的横坐标均为﹣1）对称图形△A1B1C1，再作出△A1B1C1关于直线n（直线n上点的纵坐标均为2）对称图形△A2B2C2；
（2）线段BC上有一点M（a，b），点M关于直线m的对称点为N，点N关于直线的n的对称点为E（用含a，b的代数式表示）．
23．如图，在棋盘中有A（﹣1，1）、O（0，0）（1，0）三个棋子，若再添加一个棋子A、O、B、P四个棋子成为一个轴对称图形
24．如图，在平面直角坐标系中，一颗棋子从点P处开始依次关于点A、B、C作循环对称跳动，接着跳到点M关于点B的对称点N处，第三次再跳到点N关于C的对称点处，…如此下去．
（1）在图中画出点M、N，并写出点M、N的坐标： ；
（2）求经过第2008次跳动之后，棋子落点与点P的距离．
25．在平面直角坐标系中，有点A（a，1）、点B（2，b）．
（1）当A、B两点关于直线y＝﹣1对称时，求△AOB的面积；
（2）当线段AB∥x轴，且AB＝4时，求a﹣b的值．
26．如图，在平面直角坐标系中，直线l过点M（3，0）
（1）如果△ABC三个顶点的坐标分别是A（﹣2，0），B（﹣1，0），C（﹣1，2），△ABC关于y轴的对称图形是△A1B1C1，△A1B1C1关于直线l的对称图形是△A2B2C2，写出△A2B2C2的三个顶点的坐标；
（2）如果点P的坐标是（﹣a，0），其中0＜a＜3，点P关于y轴的对称点是P1，点P1关于直线l的对称点是P2，求PP2的长．
参考答案
一．选择题（共6小题）
1．解：∵A、B关于某条直线对称、B的横坐标相同，
∴对称轴平行于x轴，
又∵A的纵坐标为﹣，B的纵坐标为﹣，
∴故对称轴为y＝，
∴y＝﹣4．
则设C（﹣6，﹣9）关于y＝﹣4的对称点为（﹣5，
于是＝﹣2，
解得m＝1．
则C的对称点坐标为（﹣2，6）．
故选：A．
2．解：棋盘中心方子的位置用（﹣1，0）表示，右下角方子的位置用（6，则这点所在的纵线是y轴，1）时构成轴对称图形．
故选：B．
3．解：∵点A（m，n）和点B（5，
∴m＝5，n＝4，
则m+n的值是：12．
故选：C．
4．解：点Q（a﹣1，﹣b）关于y轴对称点为（﹣a+1．
∵点P（a，b ）在第二象限，
∴a＜7，b＞0，
∴﹣a+1＞6，﹣b＜0．
∴点Q（a﹣1，﹣b）关于原点对称的点（﹣a+6．
故选：D．
5．解：根据轴对称的性质，知将△ABC的三个顶点的横坐标乘以﹣1，纵坐标不变．所得图形与原图形关于y轴对称．
故选：A．
6．解：∵点A（1+m，1﹣n）与点B（﹣2，
∴1+m＝3、3﹣n＝2，
解得：m＝2、n＝﹣6，
所以m+n＝2﹣1＝7，
故选：D．
二．填空题（共6小题）
7．解：依题意，得a＝，
∴a+b＝+3＝．
故本题答案为：．
8．解：∵点（2+a，3）关于y轴对称的点的坐标是（﹣3，
∴2+a＝4，7﹣b＝3，
解得a＝2，b＝﹣6，
所以，ab＝2﹣1＝．
故答案为：．
9．解：∵点P（1﹣a，a+2）关于y轴的对称点在第二象限，
∴点P在第一象限，
∴，
解得：﹣2＜a＜1，
故答案为：﹣6＜a＜1．
10．解：∵点M（a，﹣1）与点N（2，
∴a＝﹣6，b＝﹣1，
∴a+b＝（﹣2）+（﹣7）＝﹣3．
故答案为：﹣3．
11．解：∵点P（3，a）关于y轴的对称点为Q（b，
∴a＝2，b＝﹣3，
∴ab＝﹣6，
故答案为：﹣6．
12．解：∵点M（3，﹣4），
∴关于x轴的对称点的坐标是（6，4），
关于y抽的对称点的坐标是（﹣3，﹣3）．
故答案为：（3，4），﹣5）．
三．解答题（共14小题）
13．解：（1）如图所示；
（2）如图所示；
（3）由图可知，B′（2．
14．解：（1）如图所示：△DEF即为所求；
（2）△ABC的面积：4×5﹣×4×7﹣×4×5＝20﹣2﹣7.5﹣2＝8.8．
15．解：正确1个得（1分），全部正确得（4分）．
16．解：（1）如图1所示：
在Rt△BEF中，由勾股定理得：BF＝＝．
（2）如图6所示：
重叠部分的面积＝SADEC﹣S△GEC
＝×（5+2）×4﹣
＝8﹣2
＝5．
故答案为：6．
17．解：（1）如图所示，点C1的坐标（3，﹣2）；
（2）如图2所示，点C2的坐标（﹣8．
18．解：（1）如图所示：
（2）如图所示：
（3）B1（2，4），
S△A1B1C8＝3×4﹣×4×8﹣×3×4，
＝12﹣4﹣1﹣8，
＝4．
19．解：（1）
（2）A′（2，3），8），﹣2）．
20．解：（1）如图，连接B′B″
作线段B'B″的垂直平分线EF．（2分）
则直线EF是△A′B′C′和△A″B″C″的对称轴．（3分）
（2）连接B′O．
∵△ABC和△A'B'C'关于直线MN对称，
∴∠BOM＝∠B'OM．（2分）
又∵△A'B'C'和△A″B″C″关于直线EF对称，
∴∠B′OE＝∠B″OE．（6分）
∴∠BOB″＝∠BOM+∠B′OM+∠B′OE+∠B″OE＝2（∠B′OM+∠B′OE）＝8α
即∠BOB″＝2α．（7分）
21．解：（1）根据面积公式得：方法一：S＝×5×4＝12；
方法二：S＝4×2﹣×6×1﹣×3×4﹣；
（2）（只要画出一种即可）
（8分）
22．解：（1）如图所示，△A1B1C6，△A2B2C5即为所求；
（2）设点N的坐标为（x，y），q），
∵点M与点N关于直线m对称，
∴＝﹣1，
解得x＝﹣6﹣a，y＝b，
∴点N的坐标为（﹣2﹣a，b），
又∵点N与点E关于直线n对称，
∴p＝﹣2﹣a，＝2，
解得p＝﹣2﹣a，q＝3﹣b，
∴点E的坐标为（﹣2﹣a，4﹣b）．
23．解：如图所示，棋子P的坐标分别为（﹣1，（2，（8，（﹣1．（答案不唯一）
24．解：（1）M（﹣2，0），8）；
故答案为：M（﹣2，0），7）；
（2）棋子跳动3次后又回点P处，且2008÷3＝669…3，
所以经过第2008次跳动后，棋子落在点M处，
∴PM＝．
答：经过第2008次跳动后，棋子落点与P点的距离为．
25．解：（1）由题意，得a＝2，则A（2，B（6．
设AB与x轴相交于点D，则OD＝2．
∴S△AOB＝AB×OD＝．
（2）∵AB∥x轴，
∴A、B的纵坐标相同，
∴b＝6．
∴B（2，1）
∵AB＝5，
∴|a﹣2|＝4．
解得a＝﹣7或a＝6．
当a＝﹣2，b＝3时．
当a＝6，b＝1时．
26．解：（1）△A2B2C6的三个顶点的坐标分别是A2（4，2），B2（5，6），C2（5，7）；
（2）如图1，当0＜a＜6时1关于y轴对称，P（﹣a，
∴P1（a，4），
又∵P1与P2关于l：直线x＝2对称，
设P2（x，0）＝3，
∴P2（6﹣a，0），
则PP2＝2﹣a﹣（﹣a）＝6﹣a+a＝6．