2020-2021学年安徽省淮北市高二（上）期中考试数学（文）试卷北师大版

这是一份2020-2021学年安徽省淮北市高二（上）期中考试数学（文）试卷北师大版，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


1. 已知集合A={x||x|<2}，集合B={−1, 0, 1, 2, 3}，则A∩B=( )
A.{−1,0, 1}B.{0, 1, 2}C.{0, 1}D.{−1, 0, 1, 2}

2. 设向量a→=1,2，b→=m,m+1，a→⊥b→，则实数m等于（ ）
A.0B.−23C.13D.1

3. 若直线x+y=0与圆x2+y−a2=1相切，则实数a的值为（ ）
A.1B.±1C.2D.±2

4. 下列命题中，假命题是（ ）
A.∀x∈R，ex>0
B.∃x0∈R，2x0C.a+b=0的充要条件是ab=−1
D.a>1，b>1是ab>1的充分不必要条件

5. 若x，y满足 x+y≤6,2x−y≥0,y≥0, 则2x+y的最大值为（ ）
A.0B.6C.8D.12

6. 有下列命题：
①面积相等的三角形是全等三角形；
②“若xy=0，则|x|+|y|=0”的逆命题；
③“若a>b，则a+c>b+c”的否命题；
④“矩形的对角线互相垂直”的逆否命题，
其中真命题为（ ）
A.①②B.②③C.①③D.②④

7. 已知数列{an}的前n项和为Sn，且Sn=2an−1(n∈N∗)，则a5=( )
A.16B.−16C.31D.32

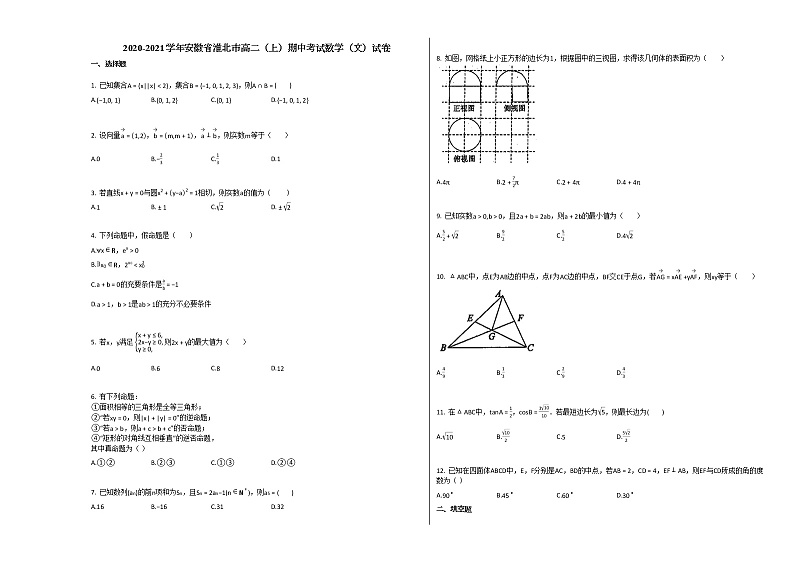
8. 如图，网格纸上小正方形的边长为1，根据图中的三视图，求得该几何体的表面积为（ ）

A.4πB.2+72πC.2+4πD.4+4π

9. 已知实数a>0,b>0，且2a+b=2ab，则a+2b的最小值为（ ）
A.52+2B.92C.52D.42

10. △ABC中，点E为AB边的中点，点F为AC边的中点，BF交CE于点G，若AG→=xAE→+yAF→，则xy等于（ ）

A.49B.13C.29D.43

11. 在△ABC中，tanA=12，csB=31010．若最短边长为5，则最长边为( )
A.10 B.102C.5D.522

12. 已知在四面体ABCD中，E，F分别是AC，BD的中点，若AB=2，CD=4，EF⊥AB，则EF与CD所成的角的度数为（ ）
A.90∘B.45∘C.60∘D.30∘
二、填空题

在正方体ABCD−A1B1C1D1中，棱长为2，点M在DD1上，点N在面ABCD上，MN=2，点P为MN的中点，则点P的轨迹与正方体的面围成的几何体的体积为________.
三、解答题

已知等比数列{an}的各项均为正数，a2=8，a3+a4=48．
(1)求数列{an}的通项公式；

(2)设bn=lg4an．证明：{bn}为等差数列，并求{bn}的前n项和Sn．

如图，在四棱锥P−ABCD中，平面PAD⊥平面ABCD，AB=AD，∠BAD=60∘，E，F分别是AP，AD的中点，求证：

(1)直线EF // 平面PCD；

(2)平面BEF⊥平面PAD．

关于x的不等式ax2+bx+3>0a,b∈R的解集为x|−3(1)求a，b的值；

(2)求关于x的不等式bx2+ax+3<0的解集．

已知a，b，c分别为△ABC三个内角A，B，C的对边，acsC+3asinC−b−c=0.
(1)求A；

(2)若a=2，△ABC的面积为3，求b，c．

已知函数f(x)=1+sinxcsx，g(x)=cs2(x+π12)．
(1)设x=x0是函数y=f(x)图象的一条对称轴，求g(x0)的值；

(2)求使函数ℎ(x)=f(ωx2)+g(ωx2)(ω>0)在区间[−2π3，π3]上是增函数的ω的最大值．

在等差数列an中，a1=8，a4=2.
(1)求数列an的通项公式；

(2)设Tn=|a1|+|a2|+⋯+|an|，求Tn.
参考答案与试题解析
2020-2021学年安徽省淮北市高二（上）期中考试数学（文）试卷
一、选择题
1.
【答案】
A
【考点】
交集及其运算
【解析】
先求出集合A和B，由此利用交集的定义能求出A∩B．
【解答】
解：∵ 集合A={x||x|<2}={x|−2B={−1, 0, 1, 2, 3}，
∴ A∩B={−1, 0, 1}．
故选A.
2.
【答案】
B
【考点】
数量积判断两个平面向量的垂直关系
【解析】
此题暂无解析
【解答】
解：由向量a→=(1,2)，b→=(m,m+1)，a→⊥b→，
可得m+2(m+1)=0，求得m=−23.
故选B.
3.
【答案】
D
【考点】
圆的切线方程
点到直线的距离公式
【解析】
由直线与圆相切，得到圆心到直线的距离等于圆的半径，利用点到直线的距离公式列出关于a的方程，求出方程的解即可得到a的值
【解答】
解：圆x2+(y−a)2=1的圆心坐标为(0, a)，半径为1，
∵ 直线x+y=0与圆x2+(y−a)2=1相切，
∴ 圆心(0, a)到直线的距离d=r，
即|a|2=1，
解得：a=±2．
故选D.
4.
【答案】
C
【考点】
命题的真假判断与应用
必要条件、充分条件与充要条件的判断
全称命题与特称命题
【解析】
对于命题A：∀x∈R,ex，根据指数函数的性质得结果正确；对于命题B：∃x0∈R,2x0ab=−1，错误，比如a=0=b时，也满足a+b=0，但是不满足ab=−1，对于命题D：ab>1可以是a>1,b>1，也可以是a<−1,b<−1，或者其中一个值大于
1，一个值小于1大于0．等等情况，故a≥1,b>1是a>1的充分不必要条件．
【解答】
解：A，∀x∈R，ex>0，根据指数函数的性质得结果正确，故A为真命题；
B，∃x0∈R，2x0C，当a+b=0且b≠0时，才能推出ab=−1，故C为假命题；
D，显然当a>1，b>1时，ab>1恒成立，故D为真命题．
故选C .
5.
【答案】
D
【考点】
求线性目标函数的最值
【解析】

【解答】
解：作出不等式组表示的可行域如图，
由图可得2x+y在B6,0处取得最大值，所以2x+ymax=12.
故选D．
6.
【答案】
B
【考点】
命题的真假判断与应用
四种命题间的逆否关系
四种命题的真假关系
【解析】
根据四种命题之间的关系分别进行判断即可．
【解答】
解：①两直角边是3和4的直角三角形与两直角边是2和6的直角三角形面积相等但是不是全等三角形，是假命题；
②“若xy=0，则|x|+|y|=0”的逆命题是“若|x|+|y|=0，则xy=0”，是真命题；
③命题“若a>b，则a+c>b+c”的否命题是“若a≤b，则a+c≤b+c”为真命题；
④“矩形的对角线互相垂直”是假命题，则其逆否命题也是假命题.
故选B.
7.
【答案】
A
【考点】
等比数列的通项公式
等比关系的确定
【解析】
先根据a1＝S1，an＝Sn−Sn−1(n≥2)求出数列{an}的通项公式，再将n＝5代入可求出所求．
【解答】
解：当n=1时，a1=S1=2a1−1，∴ a1=1．
当n>1时，Sn=2an−1，∴ Sn−1=2an−1−1，
∴ Sn−Sn−1=2an−2an−1，
∴ an=2an−2an−1，
∴ an=2an−1，
∴ anan−1=2，
∴ {an}是首项为1，公比为2的等比数列，
∴ an=2n−1，n∈N∗，
∴ a5=25−1=16．
故选A.
8.
【答案】
C
【考点】
由三视图求表面积
【解析】

【解答】
解：将三视图还原，可知原几何体由一个半径为1的半球体，与一个底面半径为1且高为1的半圆柱拼接而成．由此可得所求几何体的表面积S=12×4π+12×2π+12π×2+1×2=2+4π.
故选C．
9.
【答案】
B
【考点】
基本不等式
基本不等式在最值问题中的应用
【解析】

【解答】
解：∵ a>0，b>0，且2a+b=2ab，
∴ a=b2b−1>0，解得b>1．
则a+2b=b2b−1+2b=12+12b−1+2b
=52+12(b−1)+2(b−1)
≥52+212(b−1)⋅2(b−1)=92，
当且仅当b=32，a=32时取等号．其最小值为92．
故选B．
10.
【答案】
A
【考点】
向量在几何中的应用
【解析】

【解答】
解：由题意知G是△ABC的重心，延长AG与边BC交于点D，
则AG→=23AD→=13AB→+13AC→，
又因为点E为AB边的中点，
点F为AC边的中点，
故AB→=2AE→,AC→=2AF→，
则AG→=23AE→+23AF→，所以xy=49．
故选A．
11.
【答案】
C
【考点】
正弦定理
同角三角函数基本关系的运用
两角和与差的余弦公式
【解析】
欲求最短边的长，必须先判断谁是最短边，转化为判断谁是最小角，结合三角值即可判断最小角，接下来利用正弦定理求解即可．
【解答】
解：由tanA=12>0,
得csA=25, sinA=15,
由csB=31010>0，
得sinB=110,
于是csC=−cs(A+B)=−csAcsB+sinAsinB=−12<0,
即∠C为最大角，c为最长边，最短边为b，
于是由正弦定理bsinB=csinc求得c=5.
故选C.
12.
【答案】
D
【考点】
异面直线及其所成的角
【解析】
设G为AD的中点，连接GF，GE，利用三角形中位线定理，可证出EF⊥GF且∠FEG或其补角即为EF与CD所成角．最后在Rt△EFG中，利用正弦的定义算出∠GEF=30∘，即得EF与CD所成的角的度数．
【解答】
解：设G为AD的中点，连接GF，GE，
则GF，GE分别为△ABD，△ACD的中线．
由此可得，GF // AB且GF=12AB=1，
GE // CD，且GE=12CD=2，
∴ ∠GEF或其补角即为EF与CD所成角．
又∵ EF⊥AB，GF // AB，∴ EF⊥GF.
因此，在Rt△EFG中，GF=1，GE=2，
则sin∠GEF=GFGE=12，可得∠GEF=30∘，
∴ EF与CD所成的角的度数为30∘.
故选D.
二、填空题
【答案】
π6
【考点】
球的表面积和体积
【解析】
不论△MDN如何变化，P点到D点的距离始终等于1，从而P点的轨迹是一个以D为中心，半径为1的球的18，由此能求出结果
【解答】
解：如图，连结ND，DP，
易知ND，DM，MN构成一个直角三角形，
又P为MN的中点，MN=2，
所以根据直角三角形斜边上的中线为斜边的一半，
得无论△MDN如何变化，P点到D点的距离始终等于1，
故P点的轨迹与正方体的面围成的几何体是一个以D为球心，1为半径的球的18，
其体积=18×43×π×13=π6.
故答案为：π6.
三、解答题
【答案】
解：(1)设等比数列{an}的公比为q，依题意 q>0．
∵ a2=8，a3+a4=48，
∴ a1q=8，a1q2+a1q3=48．
两式相除得 q2+q−6=0，
解得 q=2，舍去 q=−3．
∴ a1=a2q=4．
∴ 数列{an}的通项公式为 an=a1⋅qn−1=2n+1．
(2)由(1)得 bn=lg4an=n+12．
∵ bn+1−bn=n+22−n+12=12，
∴ 数列{bn}是首项为1，公差为d=12的等差数列．
∴ Sn=nb1+n(n−1)2d=n2+3n4．
【考点】
等比数列的通项公式
等差数列的通项公式
等差数列的前n项和
【解析】
(Ⅰ)利用等比数列的通项公式即可得出；
(Ⅱ)利用(Ⅰ)的结论和对数的运算法则进行化简，再计算bn+1−bn是否是一个常数即可判定，若是利用等差数列的前n项和公式即可．
【解答】
解：(1)设等比数列{an}的公比为q，依题意 q>0．
∵ a2=8，a3+a4=48，
∴ a1q=8，a1q2+a1q3=48．
两式相除得 q2+q−6=0，
解得 q=2，舍去 q=−3．
∴ a1=a2q=4．
∴ 数列{an}的通项公式为 an=a1⋅qn−1=2n+1．
(2)由(1)得 bn=lg4an=n+12．
∵ bn+1−bn=n+22−n+12=12，
∴ 数列{bn}是首项为1，公差为d=12的等差数列．
∴ Sn=nb1+n(n−1)2d=n2+3n4．
【答案】
证明：(1)在△PAD中，
∵ E，F分别为AP，AD的中点，
∴ EF // PD.
又∵ EF不在平面PCD中，PD⊂平面PCD，
∴ 直线EF // 平面PCD．
(2)连接BD，如图，
∵ AB=AD，∠BAD=60∘．
∴ △ABD为正三角形．
∵ F是AD的中点，
∴ BF⊥AD．
∵ 平面PAD⊥平面ABCD，BF⊂平面ABCD，
平面PAD∩平面ABCD=AD，
∴ BF⊥平面PAD．
又∵ BF⊂平面EBF，
∴ 平面BEF⊥平面PAD．
【考点】
直线与平面平行的判定
平面与平面垂直的判定
【解析】
（1）要证直线EF // 平面PCD，只需证明EF // PD，EF不在平面PCD中，PD⊂平面PCD即可．
（2）连接BD，证明BF⊥AD．说明平面PAD∩平面ABCD=AD，推出BF⊥平面PAD；然后证明平面BEF⊥平面PAD．
【解答】
证明：(1)在△PAD中，
∵ E，F分别为AP，AD的中点，
∴ EF // PD.
又∵ EF不在平面PCD中，PD⊂平面PCD，
∴ 直线EF // 平面PCD．
(2)连接BD，如图，
∵ AB=AD，∠BAD=60∘．
∴ △ABD为正三角形．
∵ F是AD的中点，
∴ BF⊥AD．
∵ 平面PAD⊥平面ABCD，BF⊂平面ABCD，
平面PAD∩平面ABCD=AD，
∴ BF⊥平面PAD．
又∵ BF⊂平面EBF，
∴ 平面BEF⊥平面PAD．
【答案】
解：(1)关于x的不等式ax2+bx+3>0的解集为x|−3所以a<0，且−3和1是方程ax2+bx+3=0的两实数根，
由根与系数的关系，得−3+1=−ba，−3×1=3a，
解得a=−1,b=−2．
(2)由(1)知，a=−1,b=−2时，
不等式bx2+ax+3<0，即2x2+x−3>0，
所以2x+3x−1>0，
解得x<−32或x>1，
所以不等式bx2+ax+3<0的解集是{x|x<−32或x>1}．
【考点】
一元二次不等式的解法
一元二次不等式与一元二次方程
【解析】


【解答】
解：(1)关于x的不等式ax2+bx+3>0的解集为x|−3所以a<0，且−3和1是方程ax2+bx+3=0的两实数根，
由根与系数的关系，得−3+1=−ba，−3×1=3a，
解得a=−1,b=−2．
(2)由(1)知，a=−1,b=−2时，
不等式bx2+ax+3<0，即2x2+x−3>0，
所以2x+3x−1>0，
解得x<−32或x>1，
所以不等式bx2+ax+3<0的解集是{x|x<−32或x>1}．
【答案】
解：(1)由正弦定理知sinAcsC+3sinAsinC−sinB−sinC=0，
又sinB=sin(A+C)=sinAcsC+csAsinC，
∴ 3sinAsinC−csAsinC−sinC=0.
∵ sinC>0，
∴ 3sinA−csA−1=0，
化简得sin(A−π6)=12.
∵ −π6∴ A−π6=π6，
即A=π3；
(2)由(1)得，sinA=32，csA=12，
则由S=12bcsinA=3，
得12bc×32=3，
解得bc=4①.
由余弦定理得，a2=b2+c2−2bccsA，
即4=b2+c2−bc=(b+c)2−3bc，
解得b+c=4②，
①②联立，得b=c=2.
【考点】
两角和与差的正弦公式
余弦定理
正弦定理
【解析】
（1）利用正弦定理化简已知等式，把sinB=sin(A+C)代入并利用两角和与差的正弦函数公式化简，整理求出sin(A−π6)的值，即可确定出A的度数；
（2）利用三角形面积公式列出关系式，把sinA与已知面积代入求出bc的值，利用余弦定理列出关系式，把a，csA的值代入并利用完全平方公式变形，把bc的值代入求出+c的值，联立即可求出b与c的值．
【解答】
解：(1)由正弦定理知sinAcsC+3sinAsinC−sinB−sinC=0，
又sinB=sin(A+C)=sinAcsC+csAsinC，
∴ 3sinAsinC−csAsinC−sinC=0.
∵ sinC>0，
∴ 3sinA−csA−1=0，
化简得sin(A−π6)=12.
∵ −π6∴ A−π6=π6，
即A=π3；
(2)由(1)得，sinA=32，csA=12，
则由S=12bcsinA=3，
得12bc×32=3，
解得bc=4①.
由余弦定理得，a2=b2+c2−2bccsA，
即4=b2+c2−bc=(b+c)2−3bc，
解得b+c=4②，
①②联立，得b=c=2.
【答案】
解：(1)题设知f(x)=1+12sin2x，因为x=x0是函数y=f(x)图象的一条对称轴，
所以2x0=kπ+π2(k∈Z)，
g(x0)=12[1+cs(2x0+π6)]=12[1+cs(kπ+23π)]，
当k为偶数时，g(x0)=12(1+cs23π)=14；
当k为奇数时，g(x0)=12(1+csπ3)=34.
(2)因为ℎ(x)=(1+12sinωx)+12[1+cs(ωx+π6)]
=12(sinωx+32csωx−12sinωx)+32
=12sin(ωx+π3)+32，
当x∈[−2π3，π3]时，ωx+π3∈[−2ωπ3+π3,ωπ3+π3]，
又T2≥π3−(−2π3)=π，
所以T≥2π得ω≤1.
因为ℎ(x)在[−2π3,π3]上是增函数，且ω>0，
所以 [−2ωπ3+π3，ωπ3+π3]⊆[−π2,π2]，
即−2ωπ3+π3≥−π2,ωπ3+π3≤π2,
解得ω≤12,
所以ω的最大值为12.
【考点】
正弦函数的对称性
二倍角的正弦公式
二倍角的余弦公式
函数的求值
正弦函数的单调性
两角和与差的正弦公式
【解析】
（1）由题意可得2x0=kπ+π2，(k∈Z)，代入g(x)可得g(x0)=12[1+cs(2x0+π6)]=12[1+cs(kπ+23π)]，利用诱导公式可求
（2）由ℎ(x)=(1+12sinωx)+12[1+cs(ωx+π6)]=12sin(ωx+13π)+32，由题意可得 [−2ωπ3+π3，ωπ3+π3]⊆[−π2,π2]，可求
【解答】
解：(1)题设知f(x)=1+12sin2x，因为x=x0是函数y=f(x)图象的一条对称轴，
所以2x0=kπ+π2(k∈Z)，
g(x0)=12[1+cs(2x0+π6)]=12[1+cs(kπ+23π)]，
当k为偶数时，g(x0)=12(1+cs23π)=14；
当k为奇数时，g(x0)=12(1+csπ3)=34.
(2)因为ℎ(x)=(1+12sinωx)+12[1+cs(ωx+π6)]
=12(sinωx+32csωx−12sinωx)+32
=12sin(ωx+π3)+32，
当x∈[−2π3，π3]时，ωx+π3∈[−2ωπ3+π3,ωπ3+π3]，
又T2≥π3−(−2π3)=π，
所以T≥2π得ω≤1.
因为ℎ(x)在[−2π3,π3]上是增函数，且ω>0，
所以 [−2ωπ3+π3，ωπ3+π3]⊆[−π2,π2]，
即−2ωπ3+π3≥−π2,ωπ3+π3≤π2,
解得ω≤12,
所以ω的最大值为12.
【答案】
解：(1)数列an为等差数列，
设公差为d，
又由a1=8,a4=2
得8+3d=2⇒d=−2，
∴ an=8+n−1−2=10−2n．
(2)若10−2n≥0，则n≤5．
当n≤5时，Tn=|a1|+|a2|+⋯+|an|=a1+a2+⋯+an
=n8+10−2n2=9n−n2．
当n≥6时，
Tn=a1+a2+⋯+a5−a6−a7−⋯−an
=S5−Sn−S5=2S5−Sn=n2−9n+40，
故 Tn=9n−n2,n≤5,n2−9n+40,n≥6.
【考点】
等差数列的通项公式
等差数列的前n项和
【解析】


【解答】
解：(1)数列an为等差数列，
设公差为d，
又由a1=8,a4=2
得8+3d=2⇒d=−2，
∴ an=8+n−1−2=10−2n．
(2)若10−2n≥0，则n≤5．
当n≤5时，Tn=|a1|+|a2|+⋯+|an|=a1+a2+⋯+an
=n8+10−2n2=9n−n2．
当n≥6时，
Tn=a1+a2+⋯+a5−a6−a7−⋯−an
=S5−Sn−S5=2S5−Sn=n2−9n+40，
故 Tn=9n−n2,n≤5,n2−9n+40,n≥6.