2020-2021学年江西省抚州市高二（下）3月月考数学试卷北师大版

这是一份2020-2021学年江西省抚州市高二（下）3月月考数学试卷北师大版，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1. 观察下列各式：若a1+b1=1，a2+b2=3，a3+b3=4，a4+b4=7，a5+b5=11，⋯，则a7+b7等于( )
A.18B.29C.47D.15

2. 在Rt△ABC中，两直角边分别为a，b，斜边为c，则由勾股定理知c2=a2+b2，则在四面体P−ABC中，PA⊥PB，PA⊥PC，PB⊥PC，类比勾股定理，类似的结论为( )
A.S△PBC2=S△PAB2+S△PAC2
B.S△ABC2=S△PAB2+S△PAC2
C.S△ABC2=S△PAB2+S△PAC2+S△PBC2
D.S△PBC2=S△PAB2+S△PAC2+S△ABC2

3. 用数学归纳法证明1n+1+1n+2+...+13n≥56，从n=k到n=k+1，不等式左边需添加的项是( )
A.13k+1+13k+2+13k+3B.13k+1+13k+2+13k+3−1k+1
C.13k+1D.13k+3

4. 某个命题与自然数n有关，若n=k(k∈N∗)时命题成立，那么可推得当n=k+1时该命题也成立，现已知n=5时，该命题不成立，那么可以推得( )
A.n=6时该命题不成立B.n=6时该命题成立
C.n=4时该命题不成立D.n=4时该命题成立

5. 已知函数fx在x=1处的导数为1，则limΔx→0f1+Δx−f13Δx=( )
A.−13B.3C.13D.−32

6. 已知函数y=f(x)的图象在点M(1, f(x))处的切线方程是y=12x+2，那么f(1)+f′(1)=( )
A.12B.1C.52D.3

7. 下列求导运算正确的是( )
A.(exlnx)′=ex(1x+lnx)B.(csπ3)′=−sinπ3
C.(x2sinx)′=2xcsxD.(3x)′=3x

8. 已知fx=x3+sin3x，则其导函数f′x=( )
A.3x2+3csxB.x3+3csxC.x3+3cs3xD.3x2+3cs3x

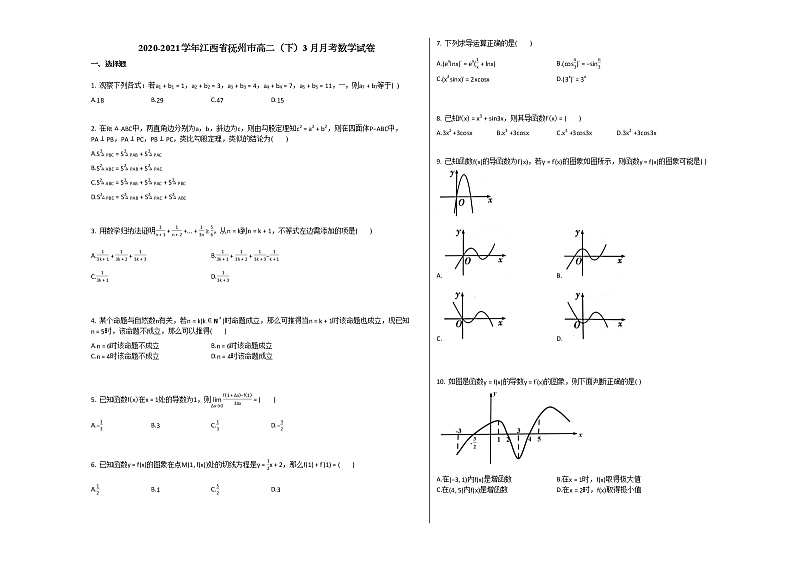
9. 已知函数f(x)的导函数为f′(x)，若y=f′(x)的图象如图所示，则函数y=f(x)的图象可能是( )

A.B.
C.D.

10. 如图是函数y=f(x)的导数y=f′(x)的图象，则下面判断正确的是( )

A.在(−3, 1)内f(x)是增函数B.在x=1时，f(x)取得极大值
C.在(4, 5)内f(x)是增函数D.在x=2时，f(x)取得极小值

11. 已知函数fx=x2−alnx+1在1,3内不是单调函数，则实数a的取值范围是( )
A.2,18B.2,18
C.−∞,2∪18,+∞D.[2,18)

12. 已知fx是定义在−∞,0∪0,+∞上的奇函数， f′x是fx的导函数， f1≠0，且满足f′xlnx+fxx1的解集为________.

已知函数f(x)=ex+alnx的定义域是D，关于函数f(x)给出下列命题：
①对于任意a∈(0, +∞)，函数f(x)是D上的减函数；
②对于任意a∈(−∞, 0)，函数f(x)存在最小值；
③存在a∈(0, +∞)，使得对于任意的x∈D，都有f(x)>0成立；
④存在a∈(−∞, 0)，使得函数f(x)有两个零点．
其中正确命题的序号是________.(写出所有正确命题的序号)
三、解答题

已知函数fx=−x3+3x+3.
(1)求函数f(x)的单调区间；

(2)求函数f(x)在0,2上的最大值和最小值.

设数列{an}满足a1=3，an+1=an2−2nan+2，n=1，2，3，⋯
(1)求a2，a3，a4的值，并猜想数列{an}的通项公式；

(2)用数学归纳法证明你的猜想．


(1)已知a>0，b>0，证明：a+b2≥2aba+b；

(2)已知a，b，c∈R+，且abc=1，证明：1a2+1b2+1c2≥a+b+c．

已知函数fx=ex−x−k2x2 ，k∈R.
(1)当k=0时，求函数fx的极值；

(2)若fx在[1,+∞）上单调递增，求实数k的取值范围．

已知函数fx=lnx−2x2，函数gx=−2x2−1x+a.
(1)求函数fx的单调区间；

(2)若对任意x∈[12,+∞)，函数fx≥gx恒成立，求实数a的取值范围．

已知函数fx=2−xex+ax2−2xa>0.
(1)讨论fx的单调区间：

(2)若fx有3个零点，求实数a的取值范围．
参考答案与试题解析
2020-2021学年江西省抚州市高二（下）3月月考数学试卷
一、选择题
1.
【答案】
B
【考点】
归纳推理
【解析】
根据给出的几个等式，不难发现，从第三项起，等式右边的常数分别为其前两项等式右边的常数的和，再写出两个等式即得．
【解答】
解：由于a1+b1=1，
a2+b2=3，
a3+b3=4，
a4+b4=7，
a5+b5=11，
⋯，
通过观察发现，从第三个式子起，等式右边的常数分别为其前两项等式右边的常数的和．
因此，a6+b6=7+11=18，a7+b7=11+18=29.
故选B.
2.
【答案】
C
【考点】
类比推理
【解析】
无
【解答】
解：平面中的边长，类比到空间中是面积，故猜想
S△ABC2=S△PAB2+S△PAC2+S△PBC2．
下面证明这个结论，画出图像如下图所示：
设PA=a，PB=b，PC=c，
△PAB，△PBC，△PAC的面积分别为S1，S2，S3，△ABC的面积为S．
则S1+S2+S3=12ab+bc+ac．
在三角形ABC中AB2=a2+b2，AC2=a2+c2，BC2=b2+c2，
cs∠BAC=a2a2+b2⋅a2+c2，
所以sin∠BAC=1−cs2∠BAC=a2b2+a2c2+b2c2a2+b2a2+c2，
所以S=12⋅AB⋅AC⋅sin∠BAC=12a2b2+a2c2+b2c2．
所以S2=S12+S22+S32，即S△ABC2=S△PAB2+S△PAC2+S△PBC2．
故选C．
3.
【答案】
B
【考点】
数学归纳法
【解析】
求出当n=k时，左边的代数式，当n=k+1时，左边的代数式，相减可得结果．
【解答】
解：当n=k时，左边的代数式为1k+1+1k+2+...+13k，
当n=k+1时，左边的代数式为1k+2+...+13k+13k+1+13k+2+13k+3，
故用n=k+1时左边的代数式减去n=k时左边的代数式的结果为13k+1+13k+2+13k+3−1k+1.
故选B.
4.
【答案】
C
【考点】
数学归纳法
【解析】
根据数学归纳法的有关概念，利用n=5时命题不成立，得出n=4时命题不成立，而n=6无法判断．由此得出正确选项．
【解答】
解：假设n=4时该命题成立，由题意可得n=5时，该命题成立，
而n=5时，该命题不成立，所以n=4时，该命题不成立．
而n=5时，该命题不成立，不能推得n=6时，该命题是否成立．
故选C．
5.
【答案】
C
【考点】
导数的运算
极限及其运算
【解析】

【解答】
解：limΔx→0f(1+Δx)−f(1)3Δx
=13limΔx→0f(1+Δx)−f(1)Δx
=13f′(1)
=13.
故选C.
6.
【答案】
D
【考点】
导数的几何意义
利用导数研究曲线上某点切线方程
【解析】
因为切点坐标一定满足切线方程，所以据此可以求出f(1)的值，又因为切线的斜率是函数在切点处的导数，就可求出f′(1)的值，把f(1)和f′(1)代入即可．
【解答】
解：∵ 点M(1, f(1))是切点，
∴ 点M在切线上，
∴ f(1)=12+2=52，
∵ 函数y=f(x)的图象在点M(1, f(1))处的切线的方程是y=12x+2，
∴ 切线斜率是12，
即f′(1)=12，
∴ f(1)+f′(1)=52+12=3．
故选D．
7.
【答案】
A
【考点】
导数的运算
【解析】
直接利用常见函数的导数公式以及导数的运算性质对各个选项逐一判断即可．
【解答】
解：A，(exlnx)′=ex(1x+lnx)，故选项A正确；
B，(csπ3)′=(12)′=0，故选项B错误；
C，(x2sinx)′=(x2)′sinx+x2(sinx)′=2xsinx+x2csx，故选项C错误；
D，(3x)′=3xln3，故选项D错误．
故选A．
8.
【答案】
D
【考点】
简单复合函数的导数
导数的运算
【解析】
此题暂无解析
【解答】
解：f′x=3x2+3cs3x.
故选D.
9.
【答案】
D
【考点】
导数的几何意义
【解析】
根据函数单调性和导数之间的关系进行判断即可．
【解答】
解：由f′(x)的图象知，当x1的解集为：x|x>0．
故答案为：x|x>0．
【答案】
②④
【考点】
利用导数研究函数的单调性
利用导数研究函数的最值
利用导数研究与函数零点有关的问题
【解析】
先求导数，若为减函数则导数恒小于零；在开区间上，若有最小值则有唯一的极小值，若有零点则对应方程有根
【解答】
解：由对数函数知：函数的定义域为：(0, +∞)，
f′(x)=ex+ax，
①∵ a∈(0, +∞)，∴ f′(x)=ex+ax≥0，f(x)是增函数．故①错误；
②∵ a∈(−∞, 0)，∴ 存在x0使f′(x0)=ex0+ax0=0，
故f(x)在0, x0上单调递减，在x0,+∞上单调递增，
∴ 对于任意a∈−∞,0，函数fx存在最小值fx0，故②正确；
函数y=ex，y=−alnx，a>0的图象在0,+∞有公共点，
∴ 对于任意a>0，fx有零点，故③错误；
由②得函数fx存在最小值fx0，
且存在a∈−∞,0，使fx0=ex0+alnx00⇒−3x2+3>0⇒−10，fx在0,+∞上单调递增，
当x0时， ex−1>0，fx在0,+∞上单调递增，
当x0，得
当x∈0,12时， f′x>0，fx单调递增，
当x∈12,+∞时，f′x0，得
当x∈0,12时， f′x>0，fx单调递增，
当x∈12,+∞时，f′x