2020-2021学年江西省赣州市高二（下）6月月考数学试卷北师大版

这是一份2020-2021学年江西省赣州市高二（下）6月月考数学试卷北师大版，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1. 已知复数z=a+bi(a，b∈R)，且共轭复数z¯=1+i1−i，则a+b=( )
A.−2B.2C.−1D.1

2. 已知向量AB→=2,4,x，平面α的一个法向量n→=1,y,3，若AB⊥α，则（ ）
A.x=6，y=2B.x=2，y=6C.3x+4y+2=0D.4x+3y+2=0

3. 把3i−x10用二项式定理展开，展开式的第8项的系数是（ ）
A.135B.−135C.−3603iD.3603i

4. 椭圆x24+y2a2=1与双曲线x2a−y22=1有相同的焦点，则a=( )
A.−1B.1C.±1D.2

5. 勾股定理是一个基本的几何定理，中国《周髀算经》记载了勾股定理的公式与证明．相传是在商代由商高发现，故又有称之为商高定理．我国古代称短直角边为“勾”，长直角边为“股”，斜边为“弦”．西方文献中一直把勾股定理称作毕达哥拉斯定理．毕达哥拉斯学派研究了勾为奇数、弦与股长相差为1的勾股数：如3，4，5；5，12，13；7，24，25；9，40，41；⋯⋯，如设勾为2n+1n∈N+，则弦为( )
A.2n2−2n+1B.4n2+1C.2n2+2nD.2n2+2n+1

6. 已知随机变量X服从正态分布Nμ,σ2，若Px>−1+Px≥5=1，则μ=( )
A.−1B.1C.−2D.2

7. 在四棱锥P−ABCD中，侧棱PA=42，底面边长AB=26，O是P在平面ABCD内的射影，M是PC的中点，则异面直线OP与BM所成角为( )
A. 30∘ B.45∘C.60∘D.90∘

8. 设a0→是与向量a→同向的单位向量，b0→是与向量a→反向的单位向量，则下列式子中不正确的是( )
A.a0→//b0→B.a→=|a→|a0→
C.a0→+b0→=0D.b0→=−a→|a→|

9. 以模型y=cekx去拟合一组数据时，为了求出回归方程，设z=lny，其变换后得到线性回归方程z=0.5x+3，则c=( )
A.3B.e3C.0.5D.e0.5

10. 设m，n>0，若随机变量ξ，η的分布列如下：
则下列说法错误的是( )
A.m+n=12B.Pξ>00C.Eξ0）的下顶点，M，N在椭圆上，若四边形OPMN为平行四边形，α为直线ON的倾斜角，若α∈π6,π4，则椭圆E的离心率的取值范围为( )
A.0,63B.0,32C.63,32D.63,223
二、填空题

01[1−(x−1)2−x ]dx=________．

某文学兴趣小组要从《飘》《围城》《红与黑》《西游记》《红楼梦》五本名著中任意选取两本，一起交流读书心得，则该小组选取的名著都是中国名著的概率为________ .

已知直线y=b分别与直线y=x−2、曲线y=2e⋅ex交于点A、B，则线段AB长度的最小值为________.

已知函数fx=ex−ax2，若fx在0,+∞只有一个零点，则a的值为________．
三、解答题

已知3x+2xn展开式中的第二项、第三项、第四项的二项式系数成等差数列．
(1)求n的值及展开式的所有项的系数和；

(2)将展开式中所有项重新排列，求有理项不相邻的概率．

小明某天偶然发现班上男同学比女同学更喜欢做几何题，为了验证这一现象是否具有普遍性，他决定在学校开展调查研究：他在全校3000名同学中随机抽取了50名，给这50名同学同等难度的几何题和代数题各一道，让同学们自由选择其中一道题作答，选题人数如表所示，但因不小心将部分数据损毁，只是记得女生选择几何题的频率是25.

(1)根据题目信息补全上表；

(2)能否根据这个调查数据判断有97.5%的把握认为选代数题还是几何题与性别有关？
参考数据和公式：

K2=nad−bc2a+bc+da+cb+d，其中n=a+b+c+d.

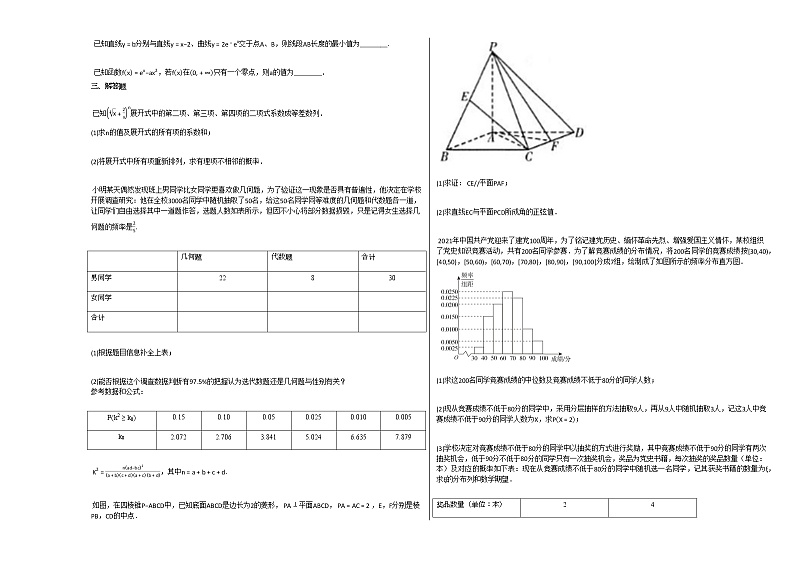
如图，在四棱锥P−ABCD中，已知底面ABCD是边长为2的菱形， PA⊥平面ABCD， PA=AC=2 ，E，F分别是棱PB，CD的中点．

(1)求证： CE//平面PAF；

(2)求直线EC与平面PCD所成角的正弦值．

2021年中国共产党迎来了建党100周年，为了铭记建党历史、缅怀革命先烈、增强爱国主义情怀，某校组织了党史知识竞赛活动，共有200名同学参赛．为了解竞赛成绩的分布情况，将200名同学的竞赛成绩按[30,40)，[40,50)，[50,60)，[60,70)，[70,80)，[80,90)，[90,100]分成7组，绘制成了如图所示的频率分布直方图．

(1)求这200名同学竞赛成绩的中位数及竞赛成绩不低于80分的同学人数；

(2)现从竞赛成绩不低于80分的同学中，采用分层抽样的方法抽取9人，再从9人中随机抽取3人，记这3人中竞赛成绩不低于90分的同学人数为X，求PX=2；

(3)学校决定对竞赛成绩不低于80分的同学中以抽奖的方式进行奖励，其中竞赛成绩不低于90分的同学有两次抽奖机会，低于90分不低于80分的同学只有一次抽奖机会，奖品为党史书籍，每次抽奖的奖品数量（单位：本）及对应的概率如下表：现在从竞赛成绩不低于80分的同学中随机选一名同学，记其获奖书籍的数量为ξ，求ξ的分布列和数学期望．

设斜率不为0的直线l与抛物线x2=4y交于A，B两点，与椭圆x26+y24=1交于C，D两点，记直线OA，OB，OC，OD的斜率分别为k1，k2，k3，k4．
(1)若直线l过0,4，证明： OA⊥OB；

(2)求证： k1+k2k3+k4的值与直线l的斜率的大小无关．

已知函数fx=x3−x−alnxa∈R.
(1)若函数fx在其定义域上为增函数，求a的取值范围；

(2)当a≤3时，求证：对任意的 x1，x2∈[1,+∞)，且 x1>x2，有2fx2−2fx1+x1−x2[f′x1+f′x2]>0恒成立．
参考答案与试题解析
2020-2021学年江西省赣州市高二（下）6月月考数学试卷
一、选择题
1.
【答案】
C
【考点】
复数的运算
共轭复数
【解析】
先求出z的共轭复数，再利用复数的运算法则和复数相等即可得出．
【解答】
解：∵z=a+bi，
∴z¯=a−bi，
∴a−bi=1+i1−i=1+i21−i1+i=2i2=i，
∴a=0，b=−1，
∴a+b=−1．
故选C．
2.
【答案】
A
【考点】
空间向量运算的坐标表示
【解析】
此题暂无解析
【解答】
解：因为AB⊥α，
所以AB→//n→，则21=4y=x3，
得x=6，y=2.
故选A．
3.
【答案】
D
【考点】
二项式定理的应用
二项式系数的性质
【解析】
此题暂无解析
【解答】
解：由题意第8项的系数为：
C107×(3i)3×(−1)7=120×33i=3603i．
故选D．
4.
【答案】
B
【考点】
椭圆的标准方程
双曲线的标准方程
【解析】
由椭圆x24+y2a2=1与双曲线x2a−y22=1有相同的焦点，则焦点在x轴上，则4−a2=a+2，且a>0,求解即可.
【解答】
解：因为椭圆x24+y2a2=1与双曲线x2a−y22=1有相同的焦点，则焦点在x轴上，
所以4−a2=a+2，且a>0，
解得a=1或a=−2（不合题意舍去）.
故选B.
5.
【答案】
D
【考点】
归纳推理
【解析】
利用勾股定理，转化求解弦即可．
【解答】
解：设斜边(弦)为x，则股为x−1,
∴x2=2n+12+x−12，
解得x=2n2+2n+1．
故选D．
6.
【答案】
D
【考点】
正态分布的密度曲线
【解析】
根据正态分布的性质得出PX≥5=PX≤−1，所以5和−1关于对称轴对称，由此即可求解．
【解答】
解：因为随机变量X服从正态分布Nμ,σ2 ，对称轴为X=μ，
又PX>−1+PX≥5=1，PX>−1+PX≤−1=1，
所以PX≥5=PX≤−1，
所以5和−1关于对称轴对称，
则μ=5+(−1)2=2．
故选D．
7.
【答案】
C
【考点】
异面直线及其所成的角
【解析】
此题暂无解析
【解答】
解：由题可知，
O是正方形ABCD的中心，
作N为OC的中点，
所以OP//MN，
则∠BMN是异面直线OP与BM所成的角.
因为OP⊥平面ABCD,
所以MN⊥平面ABCD.
因为AB=26，所以AC=BD=43，
所以BN=BO2+NO2=15，
PO=PA2−OA2=25，
所以MN=5，
所以BM=25.
因为cs∠BMN=MNBM=12，
则异面直线OP与BM所成角为60∘.
故选C.
8.
【答案】
C
【考点】
单位向量
平行向量的性质
平面向量数量积的性质及其运算
【解析】
根据单位向量的性质对四个选项进行判断，得到答案
【解答】
解：因为a0→是与向量a→同向的单位向量，b0→是与向量a→反向的单位向量，
所以a0→与b0→以及a→都共线，则a0→//b0→，故A选项正确；
因为|a→|是a→的模长，且a0→是与向量a→同向的单位向量，
所以有a→=|a→|a0→，故B选项正确；
因为a0→和b0→是方向相反的单位向量，
所以a0→+b0→=0→，故C选项错误；
因为|a→|是a→的模长，且b→是与向量a→反向的单位向量，
所以有a→=−|a→|b0→，整理得b0→=−a→|a→|，故D选项正确.
故选C．
9.
【答案】
B
【考点】
对数及其运算
求解线性回归方程
【解析】
根据指对数互化求解即可．
【解答】
解：因为z=0.5x+3，z=lny，
所以0.5x+3=lny，
所以y=e0.5x+3=e3×e0.5x．
故c=e3 .
故选B.
10.
【答案】
C
【考点】
离散型随机变量的期望与方差
离散型随机变量及其分布列
【解析】
根据离散型随机变量分布列的性质，以及离散型随机变量的期望和方差公式，根据题中所给的分布列，得到相应的结果，逐项分析，从而得到答案．
【解答】
解：A，由分布列的性质可知m+12+n=1 ，
所以m+n=12 ，故A正确；
B，Pξ>0=Pξ=2=n，
Pη>0=Pη=12+Pη=132=12+n，
因为m，n>0 ，
所以12+n>n ，即Pξ>00，故B正确；
C，Eξ=−1⋅m+0⋅12+2⋅n=2n−m，
Eη=−52⋅m+12⋅12+132⋅n=−52m+132n+14，
Eξ−Eη=32m−92n−14
=32m−9212−m−14=6m−52，
因为0x2，
令x1x2=tt>1，
则2fx2−2fx1+x1−x2f′x1+f′x2
=2x23−2x13+2x1−x2+2alnx1x2+x1−x23x12+3x22−a1x1+1x2−2
=x13−x23−3x12x2+3x1x22−ax1x2−x2x1+2alnx1x2
=x23t3−3t2+3t−1−at−1t−2lnt，
令ℎ(t)=t−1t−2lnt，t∈1,+∞，
当t>1时，ℎ′t=1+1t2−2t=1−1t2>0，
由此可得ℎ(t)在1,+∞上单调递增，
所以当t>1时，ℎ(t)>ℎ(1)，
即t−1t−2lnt>0．
因为x2≥1，t3−3t2+3t−1=t−13>0，−a≥−3，
所以x23t3−3t2+3t−1−at−1t−2lnt≥t−13−3t−1t−2lnt.
设p(t)=t−13−3t−1t−2lnt，t>1，
则p′t=3t−12−31+1t2−2t
=3t−12t2−1t2>0，
所以函数p(t)在1,+∞上单调递增，
故p(t)>p(1)=0．
综上，当a≤3时，对任意的x1，x2∈1,+∞，且x1>x2，
有2fx2−2fx1+x1−x2f′x1+f′x2>0恒成立．
【考点】
利用导数研究函数的单调性
利用导数研究不等式恒成立问题
【解析】
左侧图片未给出解析
左侧图片未给出解析
【解答】
(1)解：函数fx的定义域为0,+∞，
f′x=3x2−1−ax．
若函数fx在其定义域上为增函数，则f′x≥0在0,+∞上恒成立，
即3x2−1−ax≥0，
解得3x3−x≥a．
设g(x)=3x3−x，则g′x=9x2−1．
当x∈0,13时，g′x0，函数g(x)单调递增，
所以g(x)≥g13=−29，
所以a≤−29．
(2)证明：由(1)，得f′x=3x2−1−ax，
对任意的x1，x2∈1,+∞，且x1>x2，
令x1x2=tt>1，
则2fx2−2fx1+x1−x2f′x1+f′x2
=2x23−2x13+2x1−x2+2alnx1x2+x1−x23x12+3x22−a1x1+1x2−2
=x13−x23−3x12x2+3x1x22−ax1x2−x2x1+2alnx1x2
=x23t3−3t2+3t−1−at−1t−2lnt，
令ℎ(t)=t−1t−2lnt，t∈1,+∞，
当t>1时，ℎ′t=1+1t2−2t=1−1t2>0，
由此可得ℎ(t)在1,+∞上单调递增，
所以当t>1时，ℎ(t)>ℎ(1)，
即t−1t−2lnt>0．
因为x2≥1，t3−3t2+3t−1=t−13>0，−a≥−3，
所以x23t3−3t2+3t−1−at−1t−2lnt≥t−13−3t−1t−2lnt.
设p(t)=t−13−3t−1t−2lnt，t>1，
则p′t=3t−12−31+1t2−2t
=3t−12t2−1t2>0，
所以函数p(t)在1,+∞上单调递增，
故p(t)>p(1)=0．
综上，当a≤3时，对任意的x1，x2∈1,+∞，且x1>x2，
有2fx2−2fx1+x1−x2f′x1+f′x2>0恒成立．ξ
−1
0
2
η
−52
12
132
P
m
12
n

几何题
代数题
合计
男同学
22
8
30
女同学



合计



P(k2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
k0
2.072
2.706
3.841
5.024
6.635
7.879
奖品数量（单位：本）
2
4
概率
34
14

几何题
代数题
合计
男同学
22
8
30
女同学
8
12
20
合计
30
20
50

几何题
代数题
合计
男同学
22
8
30
女同学
8
12
20
合计
30
20
50
ξ
2
4
6
8
P
12
1748
18
148
ξ
2
4
6
8
P
12
1748
18
148