2020-2021学年安徽省高二（上）12月月考数学（理）试卷北师大版

这是一份2020-2021学年安徽省高二（上）12月月考数学（理）试卷北师大版，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


1. “xy=0”是“x=0且y=0”成立的( )
A.充分非必要条件B.必要非充分条件
C.充要条件D.既非充分也非必要条件

2. 已知△ABC的三边a、b、c所对的角分别为A、B、C，若c=acsB+bcsC，则△ABC的形状是( )
A.等腰三角形B.等边三角形
C.直角三角形D.等腰直角三角形

3. 在数列{an}中，若a1=2，an+1=an2an+1(n∈N∗)，则a5=( )
A.417B.317C.217D.517

4. 命题“若∠C=90∘，则△ABC是直角三角形”与它的逆命题、否命题、逆否命题这四个命题中，真命题的个数是( )
A.0B.3C.2D.1

5. 已知等比数列an的首项a1=e，公比q=e，则数列lnan的前10项和S10=( )
A.45B.55C.110D.210

6. 已知∀x∈R， ∃m∈R，使4x−2x+1+m=0成立，则m的取值范围是( )
A.(−∞,1]B.−∞,1C.−∞,−1D.[−1,+∞)

7. 不等式1x<12的解集是( )
A.(−∞, 0)B.(2, +∞)C.(0, 2 )D.(−∞, 0)∪(2, +∞)

8. 已知Sn是等差数列ann∈N∗的前n项和，且S5>S6>S4，以下有四个命题：
①数列an中的最大项为S10 ；②数列an的公差d<0； ③S10>0 ； ④S11<0.
其中正确的序号是( )
A.②③B.②③④C.②④D.①③④

9. 下列命题：
①“若a2②“全等三角形面积相等”的逆命题；
③“若a>1，则ax2−2ax+a+3>0的解集为R”的逆否命题；
④“若3x(x≠0)为有理数，则x为无理数”的逆否命题．
其中正确的命题是( )
A.③④B.①③C.①②D.②④

10. 设变量x，y满足约束条件x+y≥3，x−y≥−1，2x−y≤3，则目标函数z=2x+3y的最小值为( )
A.6B.7C.8D.23

11. 若对任意x>0，xx2+x+1≤a恒成立，则实数a的最小值是( )
A.13B.14C.15D.16

12. 已知数列：11，21，12，31，22，13，41，32，23，14，…，依它的前10项的规律，这个数列的第2013项a2013满足( )
A.010
二、填空题

为了应对日益严重的气候问题，某气象仪器科研单位研究出一种新的“弹射型”气候仪器，这种仪器可以弹射到空中进行气候观测，如图所示，A，B，C三地位于同一水平面上，这种仪器在C地进行弹射实验，观测点A，B两地相距100米， ∠BAC=60∘，在A地听到弹射声音比B地晚217秒(已知声音传播速度为340米/秒)，在A地测得该仪器至高点H处的仰角为30∘，则这种仪器的垂直弹射高度HC=________.

三、解答题

命题p：关于x的不等式x2+(a−1)x+a2≤0的解集为⌀，命题q：函数y=(2a2−a)x为增函数．
(1)若p是真命题，求实数a的取值范围；

(2)若“p∨q“为真命题，“p∧q”为假命题，求实数a的取值范围．

在△ABC中，A，B，C所对的边分别为a，b，c，m→=sinx,csx，n→=csx−A,sinx−A，函数fx=m→⋅n→x∈R在x=5π12处取得最大值．
(1)当x∈0,π2时，求函数fx的值域；

(2)若a=7且sinB+sinC=13314，求△ABC的面积．

如图，在四棱锥P−ABCD中，PD⊥底面ABCD，底面ABCD是正方形，E，F分别为PA，BD的中点， PD=AD=2.

(1)求证：EF//平面PBC；

(2)求二面角D−EF−P的正弦值．

已知等差数列{an}的首项为a，公差为b，且不等式lg2(ax2−3x+6)>2的解集为{x|x<1或x>b}．
(1)求数列{an}的通项公式及前n项和Sn公式；

(2)求数列{1an⋅an+1}的前n项和Tn．

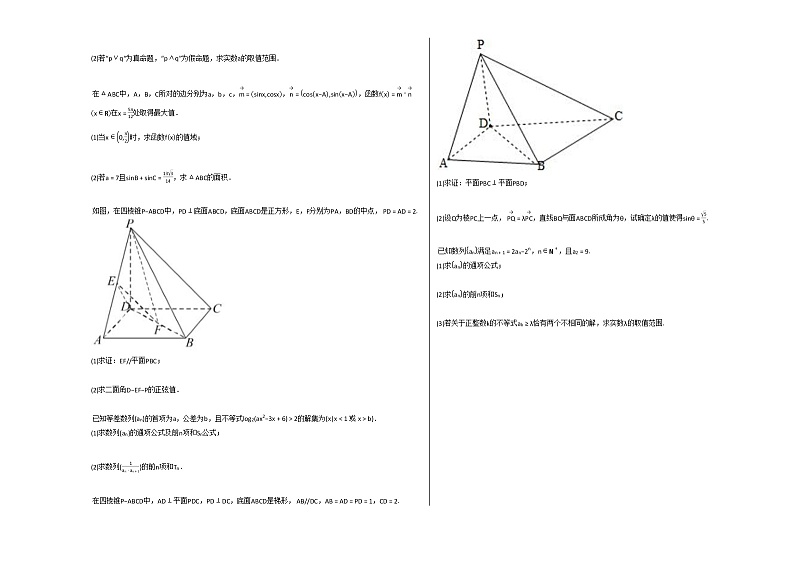
在四棱锥P−ABCD中，AD⊥平面PDC，PD⊥DC，底面ABCD是梯形， AB//DC，AB=AD=PD=1，CD=2.

(1)求证：平面PBC⊥平面PBD；

(2)设Q为棱PC上一点， PQ→=λPC→，直线BQ与面ABCD所成角为θ，试确定λ的值使得sinθ=55.

已知数列an满足an+1=2an−2n，n∈N∗，且a2=9.
(1)求an的通项公式；

(2)求an的前n项和Sn；

(3)若关于正整数k的不等式ak≥λ恰有两个不相同的解，求实数λ的取值范围.
参考答案与试题解析
2020-2021学年安徽省高二（上）12月月考数学（理）试卷
一、选择题
1.
【答案】
B
【考点】
必要条件、充分条件与充要条件的判断
【解析】
根据充分条件和必要条件的定义进行判断即可．
【解答】
解：由xy=0，可得
当x=0，y≠0时，成立；当x≠0，y=0时，成立；当x=0且y=0成立，
若x=0且y=0，则xy=0成立，
即“xy=0”是“x=0且y=0”成立的必要不充分条件.
故选B.
2.
【答案】
A
【考点】
正弦定理
【解析】
首先利用正弦定理的边角互化可得csAsinB=sinBcsC，从而csA=csC，从而可得A=C，进而可判断三角形的形状．
【解答】
解：c=acsB+bcsC，
由正弦定理得：sinC=sinAcsB+sinBcsC，
则sinA+B=sinAcsB+csAsinB
=sinAcsB+sinBcsC，
所以csAsinB=sinBcsC.
在△ABC中， 因为sinB≠0，
所以csA=csC.
又因为A，C为△ABC的内角，
所以A=C，
所以△ABC是等腰三角形．
故选A.
3.
【答案】
C
【考点】
等差数列的通项公式
【解析】
利用数列的递推关系式，求出{1an}是等差数列．然后求解即可．
【解答】
解：在数列{an}中，若a1=2，an+1=an2an+1(n∈N∗)，
可得：1an+1=2an+1an，
∴1an+1−1an=2，
∴{1an}是以首项为12，公差为2的等差数列，
∴1an=12+(n−1)×2，
解得an=24n−3，
∴ a5=217．
故选C.
4.
【答案】
C
【考点】
四种命题的真假关系
【解析】
原命题、逆否命题同真同假；逆命题、否命题同真同假
【解答】
解：∵ 原命题：“若∠C=90∘，则△ABC是直角三角形”是真命题，
∴ 逆否命题是真命题.
又∵ 逆命题:“若△ABC是直角三角形，则∠C=90∘”是假命题，
∴ 否命题是假命题，
∴ 真命题的个数是2个.
故选C.
5.
【答案】
B
【考点】
等差数列与等比数列的综合
等比数列的通项公式
等差数列的前n项和
【解析】
利用等比数列的通项公式及对数的运算得lnan为等差数列，可得解，属于基础题.
【解答】
解：由题意得：an=a1qn−1=en，lnan=lnen=n，
故lnan−lnan−1=n−n−1=1，
所以lnan为等差数列，公差为1，首项为1，
故S10=10×(1+10)2=55.
故选B.
6.
【答案】
A
【考点】
函数恒成立问题
函数的零点与方程根的关系
【解析】
由题意得方程m=−4x+2x+1有解，进而转化为函数y=m和函数y=−4x+22+1的图象有公共点，利用换元法求出函数y=−4x+22+1的值域即为所求的范围．
【解答】
解：∵ ∀x∈R，∃m∈R ，使4x−2x+1+m=0成立，
∴ 方程m=2x+1−4x有解，
∴ 函数y=m和函数y=−4x+2x+1的图象有公共点．
令t=2xt>0，
则y=−t2+2t=−t−12+1≤1，
∴ 函数y=−4x+2x+1的值域为(−∞,1]，
∴ 实数m的取值范围是(−∞,1].
故选A．
7.
【答案】
D
【考点】
分式不等式的解法
【解析】
由不等式1x<12可得x<0 或者x>0x>2 ，由此解得x的范围．
【解答】
解：由不等式1x<12得当x<0，不等式显然成立，
当x>0，解得x>2，
所以 x<0或 x>2.
故选D.
8.
【答案】
B
【考点】
等差数列的前n项和
等差数列的性质
【解析】
S5>S6>S4，可得a5>0，a6<0，a5+a6>0，d<0，再利用等差数列求和公式及其性质即可判断出结论．
【解答】
解：∵ S5>S6>S4，
∴ a5=S5−S4>0，a6=S6−S5<0，
a5+a6=S6−S4>0，
∴ d<0，②正确；
∴ 数列an中的最大项为S5，①错误；
S10=10a1+a102=5a5+a6>0，③正确；
S11=11a1+a112=11a6<0，④正确；
∴ 只有②③④正确．
故选B．
9.
【答案】
A
【考点】
四种命题间的逆否关系
【解析】
①写出“若a2②“全等三角形面积相等”的逆命题为“面积相等的三角形全等”，故可判断；
③若a>1，则△=4a2−4a(a+3)=−12a<0，可得原命题为真，故其逆否命题为真；
④“因为逆否命题为“若x为有理数，则3x为无理数”，是真命题．
【解答】
解：①“若a2取a=−2，b=1，结论不成立，故是假命题；
②“全等三角形面积相等”的逆命题为“面积相等的三角形全等”，是假命题；
③若a>1，则Δ=4a2−4a(a+3)=−12a<0，根据二次函数图像性质可知函数恒大于零，
所以“若a>1，则ax2−2ax+a+3>0的解集为R”为真命题，故其逆否命题为真；
④“若3x为有理数，则x为无理数”由无理数的定义可知该命题为真命题，
因为逆否命题为“若x为有理数，则3x为无理数”，是真命题.
故选A．
10.
【答案】
B
【考点】
求线性目标函数的最值
【解析】
试题分析：作出题中不等式组表示的平面区域，得如图的△ABC及其内部，再将目标函数z=2x+3y对应的直线进行平移，可得当x=2,y=1时，z=2x+3y取得最小值为7．
解：作出不等式组x+y≥3x−y≥12x−y≤3表示的平面区域，
得到如图的△ABC及其内部，其中A2,1,B1,2,C4,5
设z=Fx,y=2x+3y，将直线！：z=2x+3y进行平移，
当I经过点A时，目标函数z达到最小值
…最小值=F2,1=7
故选B
【解答】
解：根据题干约束条件作出平面区域（阴影部分）如下：
由z=2x+3y，变换直线方程为：y=−23x+z3，
平移直线可知在C点时，直线截距最小，此时z最小，
由x+y−3=0，2x−y−3=0，
解得C点坐标为(2,1)，
此时z的最小值为z=2×2+3×1=7.
故选B.
11.
【答案】
A
【考点】
基本不等式在最值问题中的应用
【解析】
根据基本不等式，将不等式恒成立转化为求函数的最大值即可得到结论．
【解答】
解：xx2+x+1=1x+1+1x，
∵ x>0，x+1+1x≥1+2x⋅1x=1+2=3，
当且仅当x=1x，即x=1时取等号，
∴ 0<1x+1+1x≤13，
∴ 要xx2+x+1≤a恒成立，则a≥13，
故a的最小值为13.
故选A．
12.
【答案】
A
【考点】
归纳推理
【解析】
将数列进行重新分组，根据数列项的规律即可得到结论．
【解答】
解：将数列进行重新分组，
11，(21, 12)，(31, 22, 13)，(41, 32, 23, 14)，…，
以此类推，第N大项为(N1，N−12，…，1N)，
此时有1+2+3+4+...+N=12N(N+1)，
当N=62时，共有1953项，
当N=63时，共有2016项，
所以数列的第2013项是数列第63组第60个数，
故a2013=460=115，
满足0故选A.
二、填空题
【答案】
1403米
【考点】
余弦定理的应用
解三角形的实际应用
【解析】
由题意设AC=x米，利用条件和声速表示出BC，利用余弦定理列出方程，化简后求出AC的值，在RT△ACH中，由AC和∠CAH=30∘，利用正弦函数求出答案．
【解答】
解：由题意设AC=x米，
∵ 在A地听到弹射声音的时间比B地晚217秒，
∴ BC=x−340×217=x−40.
在△ABC内，由余弦定理得：
BC2=BA2+CA2−2BA⋅CA⋅cs∠BAC，
即x−402=x2+10000−100x，
解得x=420.
在Rt△ACH中，AC=420，∠CAH=30∘，
∴ CH=AC⋅tan∠CAH=1403米，
即该仪器的垂直弹射高度HC为1403米.
故答案为：1403米．
三、解答题
【答案】
解：(1)关于x的不等式x2+(a−1)x+a2≤0的解集为⌀
等价于x2+(a−1)x+a2>0恒成立，
所以p为真命题时，Δ=(a−1)2−4a2<0，
解得a>13或a<−1.
(2)p为真时，Δ=(a−1)2−4a2<0，即a>13或a<−1．
q为真时，2a2−a>1，即a>1或a<−12．
若p∨q为真，p∧q为假，
则p、q中有且只有一个是真命题，有两种情况：
p真q假时，13p假q真时，−1≤a<−12，
∴ p、q中有且只有一个真命题时，a的取值范围为
13,1∪−1,−12.
【考点】
复合命题及其真假判断
【解析】
求出命题p，q为真命题的等价条件，结合复合命题之间的关系进行求解即可．
【解答】
解：(1)关于x的不等式x2+(a−1)x+a2≤0的解集为⌀
等价于x2+(a−1)x+a2>0恒成立，
所以p为真命题时，Δ=(a−1)2−4a2<0，
解得a>13或a<−1.
(2)p为真时，Δ=(a−1)2−4a2<0，即a>13或a<−1．
q为真时，2a2−a>1，即a>1或a<−12．
若p∨q为真，p∧q为假，
则p、q中有且只有一个是真命题，有两种情况：
p真q假时，13p假q真时，−1≤a<−12，
∴ p、q中有且只有一个真命题时，a的取值范围为
13,1∪−1,−12.
【答案】
解：(1)fx=sinxcsx−A+csxsinx−A
=sin2x−A.
因为函数在x=5π12处取得最大值，
所以2×5π12−A=π2，得A=π3，
所以fx=sin2x−π3.
因为x∈0,π2，
所以2x−π3∈−π3,2π3，
则函数值域为−32,1．
(2)因为 asinA=bsinB=csinC=732=143，
所以sinB=3b14，sinC=3c14，
则sinB+sinC=3b14+3c14=13314，
所以b+c=13．
由余弦定理得b2+c2−2bccsA=a2，
所以b+c2−2bc1+csA=a2.
又因为b+c=13，a=7，
所以bc=40，
则面积S=12bcsinA=103.
【考点】
正弦函数的定义域和值域
两角和与差的正弦公式
正弦定理
余弦定理
【解析】
（1）整理函数的解析式为fx=sin2x−π3，结合函数的定义域可得函数的值域为−32,1．
（2）利用题意首先求得b+c=13，结合余弦定理有bc=40，则△ABC的面积为103．
【解答】
解：(1)fx=sinxcsx−A+csxsinx−A
=sin2x−A.
因为函数在x=5π12处取得最大值，
所以2×5π12−A=π2，得A=π3，
所以fx=sin2x−π3.
因为x∈0,π2，
所以2x−π3∈−π3,2π3，
则函数值域为−32,1．
(2)因为 asinA=bsinB=csinC=732=143，
所以sinB=3b14，sinC=3c14，
则sinB+sinC=3b14+3c14=13314，
所以b+c=13．
由余弦定理得b2+c2−2bccsA=a2，
所以b+c2−2bc1+csA=a2.
又因为b+c=13，a=7，
所以bc=40，
则面积S=12bcsinA=103.
【答案】
(1)证明：连接AC．
因为四边形ABCD为正方形，所以F也是AC中点．
因为E为PA中点，所以EF//PC．
又PC⊂平面PBC，EF⊄平面PBC，
所以EF//平面PBC．
(2)解：因为PD⊥底面ABCD，底面ABCD是正方形，
所以AD，CD，PD两两垂直．
以D为坐标原点，DA，DC，DP所在直线为坐标轴，建立如图所示的空间直角坐标系，
则D0,0,0，E1,0,1，F1,1,0，P0,0,2，
所以DE→=1,0,1，EF→=0,1,−1，PE→=1,0,−1．
设平面DEF的一个法向量为m→=(x1,y1,z1)，
则DE→⋅m→=x1+z1=0,EF→⋅m→=y1−z1=0,
令x1=1，则y1=z1=−1，
所以m→=1,−1,−1．
设平面PEF的一个法向量为n→=x2,y2,z2，
则PE→⋅n→=x2−z2=0,EF→⋅n→=y2−z2=0,，
令x2=1，则y2=z2=1，
所以n→=1,1,1．
所以 cs⟨m→,n→⟩=m→⋅n→m→⋅n→=−13，
所以sin⟨m→,n→⟩=1−−132=223，
即二面角D−EF−P的正弦值为223．
【考点】
直线与平面平行的判定
用空间向量求平面间的夹角
【解析】
暂无
暂无
【解答】
(1)证明：连接AC．
因为四边形ABCD为正方形，所以F也是AC中点．
因为E为PA中点，所以EF//PC．
又PC⊂平面PBC，EF⊄平面PBC，
所以EF//平面PBC．
(2)解：因为PD⊥底面ABCD，底面ABCD是正方形，
所以AD，CD，PD两两垂直．
以D为坐标原点，DA，DC，DP所在直线为坐标轴，建立如图所示的空间直角坐标系，
则D0,0,0，E1,0,1，F1,1,0，P0,0,2，
所以DE→=1,0,1，EF→=0,1,−1，PE→=1,0,−1．
设平面DEF的一个法向量为m→=(x1,y1,z1)，
则DE→⋅m→=x1+z1=0,EF→⋅m→=y1−z1=0,
令x1=1，则y1=z1=−1，
所以m→=1,−1,−1．
设平面PEF的一个法向量为n→=x2,y2,z2，
则PE→⋅n→=x2−z2=0,EF→⋅n→=y2−z2=0,，
令x2=1，则y2=z2=1，
所以n→=1,1,1．
所以 cs⟨m→,n→⟩=m→⋅n→m→⋅n→=−13，
所以sin⟨m→,n→⟩=1−−132=223，
即二面角D−EF−P的正弦值为223．
【答案】
解：(1)∵ 不等式lg2(ax2−3x+6)>2可转化为ax2−3x+2>0，
所给条件表明：ax2−3x+2>0的解集为{x|x<1或x>b}，
根据不等式解集的意义，
可知方程ax2−3x+2=0的两根为x1=1，x2=b．
则1+b=3a，1⋅b=2a，
解得，a=1，b=2．
由此知an=1+2(n−1)=2n−1，Sn=n(1+2n−1)2=n2.
(2)令bn=1an⋅an+1=1(2n−1)⋅(2n+1)
=12(12n−1−12n+1).
则Tn=b1+b2+b3+…+bn
=12[(11−13)+(13−15)+(15−17)+…+(12n−1−12n+1)]
=12(1−12n+1)=n2n+1.
【考点】
数列与函数的综合
一元二次不等式与一元二次方程
等差数列的通项公式
等差数列的前n项和
数列的求和
【解析】
（1）先将不等式lg2(ax2−3x+6)>2转化为ax2−3x+2>0，所给条件表明：ax2−3x+2>0的解集为{x|x<1rx>b}，根据不等式解集的意义及方程ax2−3x+2=0的两根为x1=1、x2=b．结合利用韦达定理不难得出a，b．从而得出数列{an}的通项公式及前n项和Sn公式．
（2）令bn=1an⋅an+1=1(2n−1)⋅(2n+1)=12(12n−1−12n+1)利用拆项相消法即可求得数列{1an⋅an+1}的前n项和Tn．
【解答】
解：(1)∵ 不等式lg2(ax2−3x+6)>2可转化为ax2−3x+2>0，
所给条件表明：ax2−3x+2>0的解集为{x|x<1或x>b}，
根据不等式解集的意义，
可知方程ax2−3x+2=0的两根为x1=1，x2=b．
则1+b=3a，1⋅b=2a，
解得，a=1，b=2．
由此知an=1+2(n−1)=2n−1，Sn=n(1+2n−1)2=n2.
(2)令bn=1an⋅an+1=1(2n−1)⋅(2n+1)
=12(12n−1−12n+1).
则Tn=b1+b2+b3+…+bn
=12[(11−13)+(13−15)+(15−17)+…+(12n−1−12n+1)]
=12(1−12n+1)=n2n+1.
【答案】
(1)证明：∵ AD⊥平面PDC，PD⊂平面PDC，DC⊂平面PDC，
∴ AD⊥PD，AD⊥DC.
在梯形ABCD中，过点B作BH⊥CD于H，
在△BCH中，BH=CH=1，
∴ ∠BCH=45∘.
又∵在△DAB中，AD=AB=1，
∴ ∠ADB=45∘，
∴ ∠BDC=45∘，
∴ ∠DBC=90∘，
∴ BC⊥BD.
∵ PD⊥AD，PD⊥DC，AD∩DC=D，
AD⊂平面ABCD，DC⊂平面ABCD，
∴ PD⊥面ABCD.
∵ BC⊂平面ABCD，
∴ PD⊥BC.
∵ BD∩PD=D，BD⊂平面PBD，PD⊂平面PBD，
∴ BC⊥平面PBD.
∵BC⊂平面PBC，
∴ 平面PBC⊥平面PBD.
(2)解：以D为原点，DA，DC，DP所在直线为x，y，z轴建立空间直角坐标系，如图，
则P0,0,1，C0,2,0，A1,0,0，B1,1,0，
令Qx0,y0,z0，PQ→x0,y0,z0−1，PC→=0,2,−1，
∵ PQ→=λPC→，
∴ x0,y0,z0−1=λ0,2,−1，
∴ Q=0,2λ,1−λ，
∴ BQ→=−1,2λ−1,1−λ.
∵ DP⊥平面ABCD，
∴ n→=0,0,1是平面ABCD的一个法向量.
∵ sinθ=n→⋅BQ→|n→||BD→|=1−λ1×1+2λ−12+1−λ2.
∵ sinθ=55，
∴ 1−λ1×1+2λ−12+1−λ2=55 ，
解得λ=12．
【考点】
平面与平面垂直的判定
用空间向量求直线与平面的夹角
【解析】
（1）在梯形ABCD中，过点作B作BH⊥CD于H，通过面面垂直的判定定理即得结论；
（2）以D为原点， DA，DC，DP所在直线为x，y，z轴建立空间直角坐标系，令Qx0,y0,z0，PQ¯x0,y0,z0−1，由PQ→=λPC→，可得Q=0,2λ,1−λ，再利用空间向量法表示线面角的正弦值，得到方程解得孔即可；
【解答】
(1)证明：∵ AD⊥平面PDC，PD⊂平面PDC，DC⊂平面PDC，
∴ AD⊥PD，AD⊥DC.
在梯形ABCD中，过点B作BH⊥CD于H，
在△BCH中，BH=CH=1，
∴ ∠BCH=45∘.
又∵在△DAB中，AD=AB=1，
∴ ∠ADB=45∘，
∴ ∠BDC=45∘，
∴ ∠DBC=90∘，
∴ BC⊥BD.
∵ PD⊥AD，PD⊥DC，AD∩DC=D，
AD⊂平面ABCD，DC⊂平面ABCD，
∴ PD⊥面ABCD.
∵ BC⊂平面ABCD，
∴ PD⊥BC.
∵ BD∩PD=D，BD⊂平面PBD，PD⊂平面PBD，
∴ BC⊥平面PBD.
∵BC⊂平面PBC，
∴ 平面PBC⊥平面PBD.
(2)解：以D为原点，DA，DC，DP所在直线为x，y，z轴建立空间直角坐标系，如图，
则P0,0,1，C0,2,0，A1,0,0，B1,1,0，
令Qx0,y0,z0，PQ→x0,y0,z0−1，PC→=0,2,−1，
∵ PQ→=λPC→，
∴ x0,y0,z0−1=λ0,2,−1，
∴ Q=0,2λ,1−λ，
∴ BQ→=−1,2λ−1,1−λ.
∵ DP⊥平面ABCD，
∴ n→=0,0,1是平面ABCD的一个法向量.
∵ sinθ=n→⋅BQ→|n→||BD→|=1−λ1×1+2λ−12+1−λ2.
∵ sinθ=55，
∴ 1−λ1×1+2λ−12+1−λ2=55 ，
解得λ=12．
【答案】
解：(1)因为an+1=2an−2n，
所以an+12n+1=an2n−12，
所以an+12n+1−an2n=−12，
所以an2n是公差为−12的等差数列，
且a2=2a1−2，
所以a1=112，
且a121=114，
所以an2n=114+(n−1)−12，
所以an=134−n2⋅2n．
(2)因为Sn=114⋅21+94⋅22+74⋅23+⋯+13−2n4⋅2n，
所以2Sn=114⋅22+94⋅23+74⋅24+⋯+13−2n4⋅2n+1，
所以−Sn=114⋅21+−12⋅22+−12⋅23+⋯
+−12⋅2n−13−2n4⋅2n+1，
所以Sn=−114⋅21+21+22+⋯+2n−1+13−2n4⋅2n+1
=−112+2(1−2n−1)1−2+13−2n4⋅2n+1，
所以Sn=−112+(2n−2)+13−2n4⋅2n+1
=15−2n4⋅2n+1−152．
(3)因为an=134−n2⋅2n，
所以an+1=134−n+12⋅2n+1，
所以an+1−an
=134−n+12⋅2n+1−134−n2⋅2n
=94−n2⋅2n，
当n≤4时，an+1−an>0，
所以{an}递增，
当n≥5时，an+1−an<0，
所以{an}递减，
所以a1a6>a7>⋯⋯，
所以(an)max=a5=24，
且a4=20，a6=16，a3=14，
又因为ak≥λ恰有两个不同的解，
所以可知k=4，5，
所以a6<λ≤a4，
所以λ∈(16,20]．
【考点】
等差数列的通项公式
等差数列
数列的求和
数列与函数的综合
数列与函数最值问题
【解析】
左侧图片未给出解析．
左侧图片未给出解析．
左侧图片未给出解析．
【解答】
解：(1)因为an+1=2an−2n，
所以an+12n+1=an2n−12，
所以an+12n+1−an2n=−12，
所以an2n是公差为−12的等差数列，
且a2=2a1−2，
所以a1=112，
且a121=114，
所以an2n=114+(n−1)−12，
所以an=134−n2⋅2n．
(2)因为Sn=114⋅21+94⋅22+74⋅23+⋯+13−2n4⋅2n，
所以2Sn=114⋅22+94⋅23+74⋅24+⋯+13−2n4⋅2n+1，
所以−Sn=114⋅21+−12⋅22+−12⋅23+⋯
+−12⋅2n−13−2n4⋅2n+1，
所以Sn=−114⋅21+21+22+⋯+2n−1+13−2n4⋅2n+1
=−112+2(1−2n−1)1−2+13−2n4⋅2n+1，
所以Sn=−112+(2n−2)+13−2n4⋅2n+1
=15−2n4⋅2n+1−152．
(3)因为an=134−n2⋅2n，
所以an+1=134−n+12⋅2n+1，
所以an+1−an
=134−n+12⋅2n+1−134−n2⋅2n
=94−n2⋅2n，
当n≤4时，an+1−an>0，
所以{an}递增，
当n≥5时，an+1−an<0，
所以{an}递减，
所以a1a6>a7>⋯⋯，
所以(an)max=a5=24，
且a4=20，a6=16，a3=14，
又因为ak≥λ恰有两个不同的解，
所以可知k=4，5，
所以a6<λ≤a4，
所以λ∈(16,20]．