2020-2021年江西省赣州市高三（上）期末考试数学（文）试卷北师大版

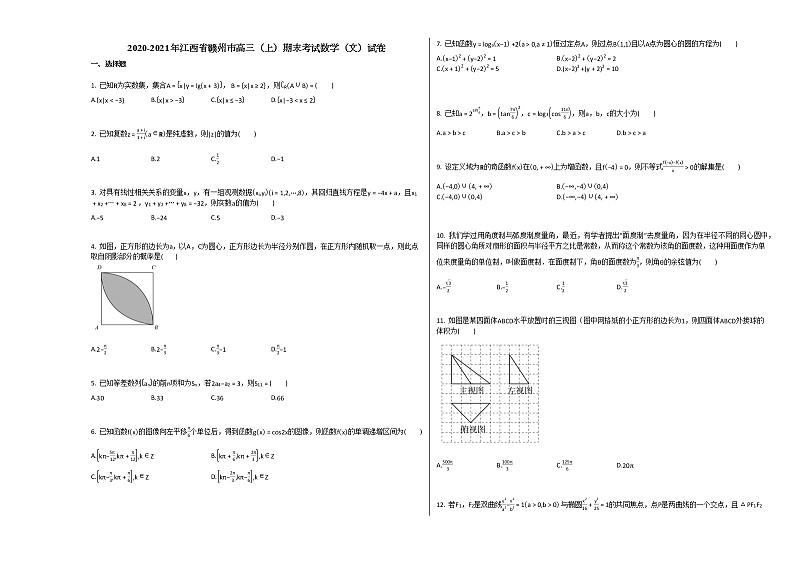
这是一份2020-2021年江西省赣州市高三（上）期末考试数学（文）试卷北师大版，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1. 已知R为实数集，集合A=x|y=lgx+3， B=x|x≥2，则∁RA∪B=( )
A.{x|x−3C.x|x≤−3D.x|−30,a≠1恒过定点A，则过点B1,1且以A点为圆心的圆的方程为( )
A.x−12+y−22=1B.x−22+y−22=2
C.x+12+y−22=5D.(x−2)2+(y+2)2=10

8. 已知a=2sinπ6，b=tan7π62，c=lg3cs11π6，则a，b，c的大小为( )
A.a>b>cB.a>c>bC.b>a>cD.b>c>a

9. 设定义域为R的奇函数fx在0,+∞上为增函数，且f−4=0，则不等式f−x−fxx>0的解集是( )
A.−4,0∪4,+∞B.−∞,−4∪0,4
C.−4,0∪0,4D.−∞,−4∪4,+∞

10. 我们学过用角度制与弧度制度量角，最近，有学者提出“面度制”去度量角，因为在半径不同的同心圆中，同样的圆心角所对扇形的面积与半径平方之比是常数，从而称这个常数为该角的面度数，这种用面度作为单位来度量角的单位制，叫做面度制．在面度制下，角θ的面度数为π3，则角θ的余弦值为( )
A.−32B.−12C.12D.32

11. 如图是某四面体ABCD水平放置时的三视图（图中网格纸的小正方形的边长为1，则四面体ABCD外接球的体积为( )

A.500π3B.100π3C.125π6D.20π

12. 若F1，F2是双曲线y2a2−x2b2=1a>0,b>0 与椭圆x216+y225=1的共同焦点，点P是两曲线的一个交点，且△PF1F2为等腰三角形，则该双曲线的渐近线方程是( )
A.y=±22xB.y=±24xC.y=±73xD.y=±377x
二、填空题

已知向量a→=m,−1，b→=−2,−m+1，若a→⊥a→+b→，则m=________.

若曲线y=xlnx+1在x=1处的切线与直线2ax−a−1y+3=0垂直，则a=________.

已知不等式 x−y≤03x−y−2≥0x+y−6≤0 表示的平面区域为D，若存在x,y∈D，使得不等式x−2y−t≥0成立，则实数t的最大值为________.

已知数列an的首项a1=2，前n项和为Sn，且Sn+Sn+1=2n+1−1n∈N∗，则S11=________.
三、解答题

在△ABC中，角A，B，C所对的边分别为a，b，c，且acsB=2c−bcsA.
(1)求A；

(2)已知b=3，若AB→+AC→=2AM→且 |AM→|=132，求△ABC的面积．

如图，一简单组合体的一个面ABC内接于圆O，AB是圆O的直径，矩形BCDE所在的平面垂直于圆O所在的平面．

(1)证明：平面ADE⊥平面ADC；

(2)若AB=2，AC=1，∠EAB=45∘ ，试求该简单组合体的体积．

2021届高考体检工作即将开展，为了了解高三学生的视力情况，某校医务室提前对本校的高三学生视力情况进行调查，在高三年级1000名学生中随机抽取了100名学生的体检数据，并得到如图的频率分布直方图．

(1)若直方图中前四组的频数依次成等比数列，试估计全年级高三学生视力的中位数（精确到0.01）；

(2)该校医务室发现，学习成绩突出的学生，近视的比较多，为了研究学生的视力与学习成绩是否有关系，对抽取的100名学生名次在1∼100名和101∼1000名的学生的体检数据进行了统计，得到如表中的数据，根据表中的数据，能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系？

(3)在(2)中调查的不近视的学生中按照分层抽样抽取了6人，进一步调查他们良好的护眼习惯，求在这6人中任取2人，至少有1人的年级名次在1∼100名的概率．
K2=nad−bc2a+bc+da+cb+d，其中n=a+b+c+d.

已知函数fx=exx−k1x+lnx，其中k为常数， e=2.71828⋯为自然对数的底数．
(1)若k=e2，求函数fx的极值；

(2)若函数fx在区间1,2上单调，求k的取值范围．

如图，已知抛物线M:x2=2pyp>0的焦点为F0,1，过焦点F作直线交抛物线于A，B两点，在A，B两点处的切线相交于N，再分别过A，B两点作准线的垂线，垂足分别为C，D．

(1)求证：点N在定直线上；

(2)是否存在点N，使得△BDN的面积是△ACN的面积和△ABN的面积的等差中项，若存在，请求出点N的坐标，若不存在，请说明理由．

在直角坐标系xOy中，已知过点Pm,0的直线l的参数方程是x=m+22t,y=22t, （t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=2csθ．
(1)求直线l的普通方程和曲线C的直角坐标方程；

(2)若直线l和曲线C交于A，B两点，且|PA|⋅|PB|=1，求实数m的值．
参考答案与试题解析
2020-2021年江西省赣州市高三（上）期末考试数学（文）试卷
一、选择题
1.
【答案】
C
【考点】
交、并、补集的混合运算
【解析】
化简集合A，再利用集合的运算求解即可.
【解答】
解：∵ 集合A=x|y=lgx+3 ={x|x>−3}，
B=x|x≥2，
∴ A∪B={x|x>−3}，
则∁RA∪B= x|x≤−3 .
故选C.
2.
【答案】
A
【考点】
复数代数形式的乘除运算
复数的模
【解析】
设a+i1+i=bi，其中b∈R，b≠0，则a+i=−b+bi，解得a=−1，b=1．再由复数模的计算公式求解．
【解答】
解：设a+i1+i=bi，其中b∈R，b≠0，
则a+i=−b+bi，
解得b=1，a=−1，
∴z=i，
则|z|=1.
故选A.
3.
【答案】
D
【考点】
求解线性回归方程
【解析】
利用回归直线方程为y=−4x+a经过样本中心值(14，−4)，求解即可.
【解答】
解：∵ x¯=18(x1+x2+…+x8)=14，
y¯=18(y1+y2+…+y8)=−4，
∴ 回归直线方程为y=−4x+a经过(14,−4)，
∴ −4=−4×14+a，
解得a=−3.
故选D.
4.
【答案】
D
【考点】
几何概型计算（与长度、角度、面积、体积有关的几何概型）
【解析】
将阴影部分拆分成两个小弓形，从而可求解出阴影部分面积，根据几何概型求得所求概率．
【解答】
解：阴影部分可拆分为面积相等的两部分，
则阴影部分面积S阴影部分=2×(14πa2−12a2)=12πa2−a2，
正方形面积S=a2，
∴ 所求概率P=S阴影部分S=π2−1，
故选D．
5.
【答案】
B
【考点】
等差数列的前n项和
等差中项
【解析】
利用等差数列通项得到a1+5d=a6=3，再利用等差数列性质与求和即可得到答案.
【解答】
解：设等差数列an的公差为d.
∵ 2a4−a2=3，
∴ 2(a1+3d)−(a1+d)=3，
即a1+5d=a6=3，
∴ S11=11×a1+a112=11a6=33.
故选B.
6.
【答案】
C
【考点】
余弦函数的单调性
函数y=Asin（ωx+φ）的图象变换
【解析】
注意三角函数单调性
【解答】
解：将函数g(x)=cs2x的图像向右平移π6个单位得到
fx=cs2x−π6=cs2x−π3.
又∵ 余弦函数的单调递增区间为 −π+2kπ,2kπ,k∈Z，
∴ −π+2kπ≤2x−π3≤2kπ，
即−2π3+2kπ≤2x≤π3+2kπ ，
∴ −π3+kπ≤x≤π6+kπk∈Z
∴fx 的单调递增区间为 −π3+kπ,π6+kπ(k∈Z)．
故选C．
7.
【答案】
B
【考点】
点与圆的位置关系
对数及其运算
【解析】
此题暂无解析
【解答】
解：因为 y=lgax−1+2a>0,a≠1，且lga1=0，
则y=lgax−1恒过2,0，
所以y=lgax−1+2恒过(2,2)，
所以A(2,2).
设圆的半径为r，则以定点(2,2)为圆心的圆方程为
(x−2)2+(y−2)2=r2 ,
因为该圆还过点B(1,1)，
所以r2=2，
则过点B1,1且以A点为圆心的圆的方程为
(x−2)2+(y−2)2=2 .
故选B．
8.
【答案】
A
【考点】
根式与分数指数幂的互化及其化简运算
诱导公式
指数式、对数式的综合比较
【解析】
分别对条件中的三个数化简，
判断出它们的值的大致范围即可.
【解答】
解：∵a=2sinπ6=212=2>1，
b=tan7π62=−tanπ62=−332=13，
c=lg3cs11π6=lg3csπ6=lg332b>c.
故选A.
9.
【答案】
C
【考点】
函数奇偶性的性质
函数单调性的性质
【解析】
根据函数为奇函数，将原不等式作等价转换为xfx0⇔−2fxx>0⇔xfx