2021学年4二次函数性质的再研究课堂教学ppt课件

这是一份2021学年4二次函数性质的再研究课堂教学ppt课件，共19页。PPT课件主要包含了图2-20，yx2，y2x2，y05x2，如图2-22，知识小结等内容，欢迎下载使用。

在初中,我们已经学过了二次函数,知道其图像为抛物线,并了解其图像的开口方向、对称轴、顶点等特征.
下面我们进一步研究一般的二次函数f(x)=ax2 +bx+c (a≠0).
探究：(1) y=x2和y=ax2 (a≠0)的图像之间有什么关系?
1.我们先画出y=x2的图像,并在此基础上画出y=2x2的图像.
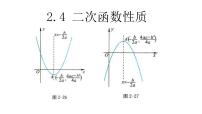
y=x2的图像如图2-20.
我们再在此基础上画y=2x2的图像.
先列表(如表2-7):
从表中不难看出,要得到2x2的值，只要把相应的x2的值扩大为原来的2倍就可以了.
这种情况表现在图像上，如图2-20,就是把AB伸长为原来的2倍，即AC的长度,得到当x=1时y=2x2对应的值.同理,其余x值对应的x2的值,都扩大为原来的2倍,就可以得到y=2x2的图像了(如图2-21).
请用类似的方法,画出y= x2和y=- 2x2的图像.
二次函数y= ax2 (a≠0)的图像可由y=x2的图像各点的纵坐标变为原来的a倍得到.
从图中还可以看出,a决定了图像的开口方向和在同一直角坐标系中的开口大小
探究：(2) y=ax2和y=a(x+h)2+k(a≠0)的图像之间有什么关系?
我们一起回顾y=2x2与y=2(x+ 1)2 +3图像的关系. 在初中我们已经知道,只要把y=2x2的图像向左平移1个单位长度,【y=2(x+1)2 】再向上平移3个单位长度, 就可以得到y=2(x+1)2+3的图像.它们形状相同,位置不同
(1)由y=-3x2的图像,画出y=-3(x- 1)2+1的图像.(2) 想象一下并回答:由y=-3x2的图像，如何得到y=一3(x+2)2- 1的图像?(3)想象一下并回答:把y=3x2的图像,向右平移2个单位长度,再向上平移5个单位长度,能得到哪个函数的图像?
只要把y=-3x2的图像向左平移2个单位长度,再向下平移1个单位长度,
y=一3(x-2)2+5
一般地,二次函数 y=a(x+h)2+k(a≠0),a决定了二次函数图像的开口大小及方向;h决定了二次函数图像的左右平移,而且“h正左移,h负右移”;k决定了二次函数图像的上下平移,而且“k正上移，k负下移”。
(2) y=ax2和y=a(x+h)2+k(a≠0)的图像之间有什么关系?
(3) y=ax2和y=ax2 +bx +c(a≠0)的图像之间有什么关系?
3.我们再一起回顾一下y=2x2与y=2x2 +4x-1图像的关系.我们在初中时就知道,为研究y=2x2 +4x- 1的图像,应该通过配方把它化成我们已经掌握的y=a(x+h)2+k的形式,即y= 2x2+4x- 1= 2(x2+2x)- 1= 2(x2+2x+1- 1)- 1= 2[(x+ 1)2- 1]- 1=2(x+1)2- 3.至此,我们就知道,把y=2x2的图像左移1个单位长度,再下移3个单位长度,就可得到y=2x2 +4x-1的图像(如图2-23).
一般地,二次函数 y=ax2 +bx+c(a≠0) ,通过配方可以得到它的恒等形式y=a(x +h)2+k,从而知道,由y=ax2的图像如何平移就得到它(y=ax2 +bx +c(a≠0))的图像.
上面,我们经历了y=x2到y=ax2 ,y=ax2到y=a(x+h)2+k,y=ax2到y=ax2 +bx +c(其中,a均不为0)的图像变化过程.通过这个过程,我们就能体会到研究一般函数图像的拓展过程.
例1二次函数 f(x)与g(x)的图像开口大小相同，开口方向也相同,已知函数g(x)的解析式和f(x)图像的顶点,写出函数f(x)的解析式:(1)函数g(x)=x2, f(x)图像的顶点是(4, -7);(2)函数g(x)=- 2(x+1)2 ,f(x)图像的顶点是(一3, 2).
解 如果二次函数的图像与 y=ax2的图像开口大小相同,开口方向也相同，顶点坐标是(-h, k),则其解析式为y=a(x+h)2+k.(1)因为f(x)与g(x)=x2的图像开口大小相同,开口方向也相同，f(x)图像的顶点是(4，-7),所以f(x)=(x-4)2-7=x2-8x+9;
(2)因为f(x)与g(x)=-2(x+1)2的图像开口大小相同,开口方向也相同,g(x)=-2(x+1)2又与y=-2x2的图像开口大小相同,开口方向也相同,所以f(x)与y=-2x2的图像开口大小也相同,开口方向也相同.又因为f(x)图像的顶点是(一3, 2),所以f(x)=-2(x+3)2+2=-2x2- 12x- 16.
例1二次函数 f(x)与g(x)的图像开口大小相同，开口方向也相同,已知函数g(x)的解析式和f (x)图像的顶点,写出函数f(x)的解析式:(1)函数g(x)=x2, f(x)图像的顶点是(4, -7);(2)函数g(x)=- 2(x+1)2 ,f(x)图像的顶点是(一3, 2).
y=ax2和y=a(x+h)2+k(a≠0)的图像之间关系
作业：已知二次函数f(x)满足f(2)＝－1，f(－1)＝－1，且f(x)的最大值是8，求此二次函数的解析式．