初中数学浙教版七年级上册3.1 平方根教案配套ppt课件

这是一份初中数学浙教版七年级上册3.1 平方根教案配套ppt课件，共22页。PPT课件主要包含了想一想，填一填，平方运算，0的平方根是，-4的平方根不存在，说一说，负数没有平方根，零的平方根是零，理一理，非负数才有平方根等内容，欢迎下载使用。
要给一幅面积为1.44平方米的正方形油画镶上边框
( ) 2 = 6.25
( ) 2 =
( ) 2 = 121
一般地，如果一个数的平方等于a，那么这个数叫做a的平方根，也叫做a的二次方根.
又因为 (－1.2 )2 = 1.44， 所以 －1.2 也是1.44的平方根.
例如， 1.2 2 = 1.44， 所以 1.2是1.44的平方根;
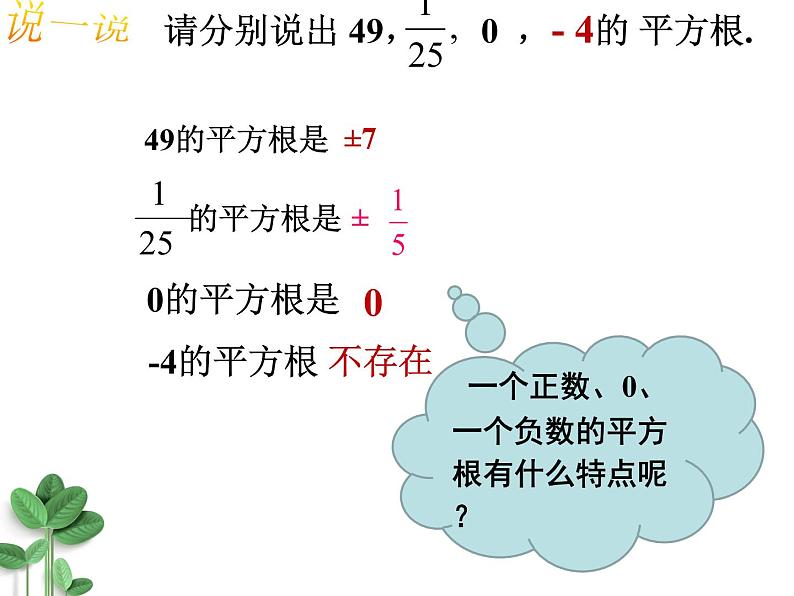
请分别说出 49， 0 ，- 4的 平方根.
49的平方根是
一个正数、0、一个负数的平方 根有什么特点呢？
关于数的平方根，有以下事实：
一个正数有正、负两个平方根，它们互为相反数；
让我们一起来表示一个数的平方根：
即：正数a的平方根表示为
（a是非负数,即a≥0 ）
古时候，埃及人用记号“┌”表示平方根；印度人在开平方时，在被开方数的前面写上ka；1840年前后，德国人用一个点“.”来表示平方根；直到十七世纪，法国数学家笛卡尔（1596～1650年）第一个使用了现今用的根号“√￣”.
例1 . 求下列各数的平方根：
(3) ∵（±0.6）²=0.36
求一个数的平方根的运算叫做
遇带分数先化成假分数再开方
不要遗漏根号前面的“±”号
开平方是平方运算的逆运算
1、课本P70“课内练习”的第 1 题;
填空（课内练习一）: (1)
∵（ ）²=64
∵ （ ）²=0.04
，∴ .
2、课本P70“课内练习”的第 2 题.
一幅面积为1.44平方米的正方形油画，它的边长是多少？
在实际生产和生活中，往往需要正的平方根.
正数的正平方根称为算术平方根.
非负数a的算术平方根表示为：
比如，9的算术平方根是3，
例2: 说出下列各式的意义,再计算:
练习二：课本P71“作业题”的第 4 题.
算术平方根 的双重非负性
一个正数有正、负两个平方根，它们互为相反数；零的平方根是零；负数没有平方根.
正数的正平方根和零的平方根,统称为算术平方根.
求一个数的平方根的运算叫做开平方．
2、关于平方根的事实：
如果x2=a，则x是a的平方根.
加法——和； 减法——差乘法——积； 除法——商乘方——幂； 开方——方根（后者是前者的逆运算！）
平方根与算术平方根有何联系与区别?区别:(1)定义不同 ; (2)个数不同.联系:(1)平方根中包含算术平方根,算术平方根 是平方根的一个;(2)平方根与算术平方根的被开方数都是非负数;(3)0的平方根与算术平方根都是0.
计算下列各式的值：（1） （2） （3） （4）
有人说可以通过添加运算符号使得下列等式成立，你能做到吗？ 4 4 4 = 6 9 9 9 = 6