北师大版八年级上册4 估算示范课ppt课件

这是一份北师大版八年级上册4 估算示范课ppt课件，共17页。PPT课件主要包含了×40800，结果精确到1，结果精确到01，如何取结果，夹逼法，估算方法，思路呈现，用估算来解决实际问题，不能办到等内容，欢迎下载使用。

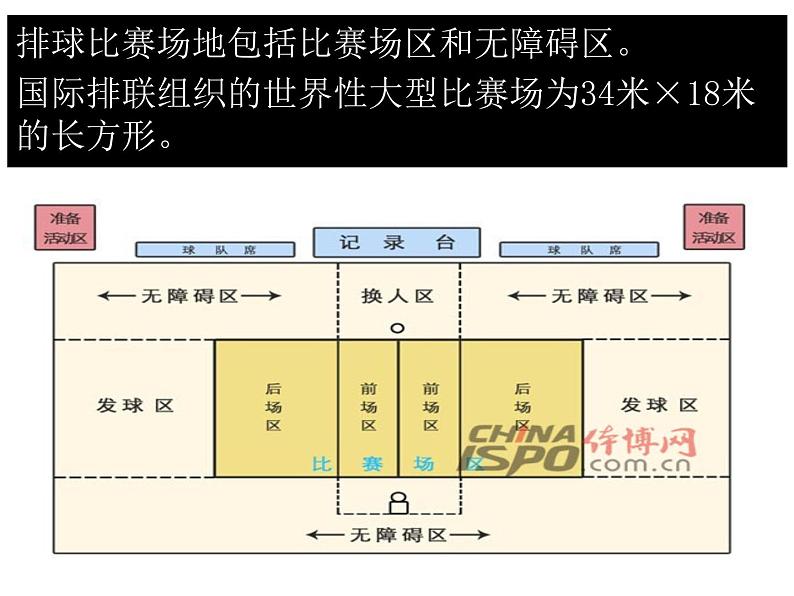
排球比赛场地包括比赛场区和无障碍区。国际排联组织的世界性大型比赛场为34米×18米的长方形。
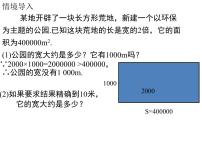
(2)若设荒地的宽是xm？如何求解？
(1)荒地宽大约多少？有20m吗？
现有一块长方形荒地来建排球场，已知这块地的长是宽的两倍，它的面积为740m2.
学习目标：估算一个无理数的范围，用来解决实际问题
解:设荒地的宽为 m,则它的长为 m.
用估算来解决实际问题：可以修建排球比赛场
估算无理数大小的要点：
(1)利用乘方与开方互为逆运算，将无理数转化为有理数
(2)通过这个有理数确定无理数的整数部分
(3)根据所要求的精确度确定小数部分
特别注意：估算过程中，不断尝试实验，观察规律并思考做出判断。
1.估算一个无理数的范围的方法：
2.小学估算方法：四舍五入，去尾法，进一法，凑整法等。实际生活中常用到取大取小法。
1.判断下列估算结果正确吗？你怎么想的？
判断方法：乘方与开方互逆运算

2.你能估算它们的大小吗？（①②④结果精确到1,③结果精确到10）.
1.生活经验表明，靠墙摆放梯子时，若梯子底端离墙距离为梯子长度的三分之一，则梯子比较稳定。现有一长度为6米的梯子，当梯子稳定摆放时，（1）梯子的顶端最多能到达多高（结果精确到0.1）? （2）现在如果请一个同学利用这个梯子在墙高5.9米的地方张贴一副宣传画，他能办到吗？
解：设梯子稳定摆放时的高度为x m， 此时梯子底端离墙恰好为梯子
3. 一个人一生平均要饮用的液体总量大约为40立方米 .如果用一圆柱形的容器（底面直径等于高）来装这些液体，这个容器大约有多高（误差小于1米）?
2.一个人一生平均要饮用的液体总量大约为40立方米 .如果用一圆柱形的容器（底面直径等于高）来装这些液体，这个容器大约有多高（结果精确到1）?器大约有多高（误差小）? 解：设圆柱的高为x，那么它的底面半径为0.5x,则: ∴X ≈ 4
数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：求59319的立方根．华罗庚脱口而出：39．众人十分惊奇，忙问计算的奥妙．
请你按下面的问题试一试：（1）103=1000，1003=1000000，你能确定59319的立方根是几位数吗？答： 位数．（2）由59319的个位数是9，你能确定59319的立方根的个位数是几吗？答： （3）如果划去59319后面的三位319得到数59，而33=27，43=64，由此你能确定59319的立方根的十位数是几吗？答： ；因此59319的立方根是
1.判断无理数估算结果的合理性
2.学会估算一个无理数的大致范围
3.用估算来解决实际问题
说一说这节课你学到了什么？
4.拥有良好估算意识，发展数感