




冀教版七年级上册2.7 角的和与差授课课件ppt
展开1.结合具体图形,掌握角的和与差的意义,并会进行角的和与差运算。2.掌握角平分线的性质及掌握角平分线的性质的应用。重点:掌握角平分线的意义及会运用角平分线的意义
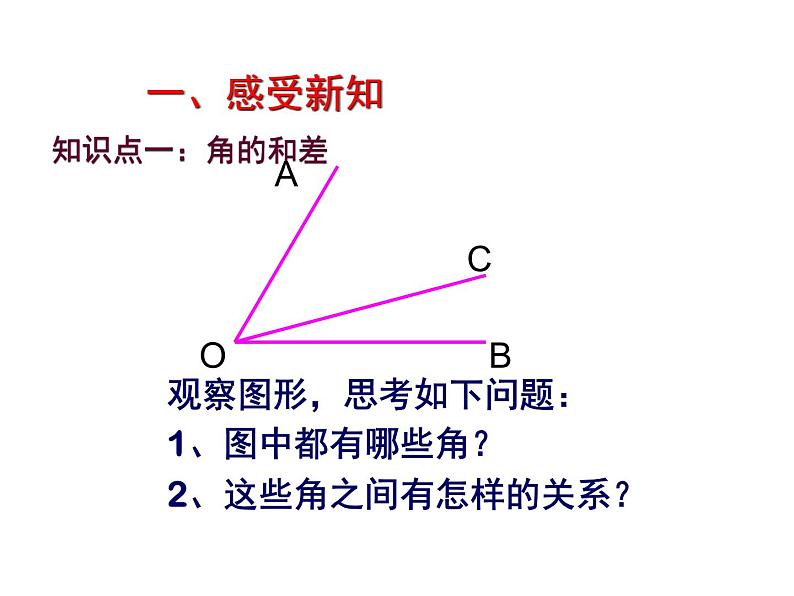
知识点一:角的和差
观察图形,思考如下问题:1、图中都有哪些角?2、这些角之间有怎样的关系?
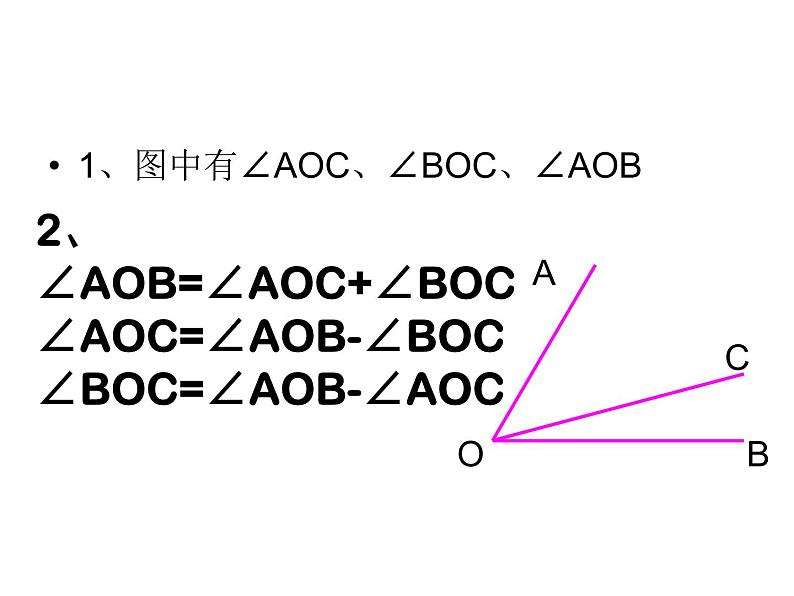
1、图中有∠AOC、∠BOC、∠AOB
2、∠AOB=∠AOC+∠BOC∠AOC=∠AOB-∠BOC∠BOC=∠AOB-∠AOC
如图,填出符合下列等式的角。(1)∠AOC+∠BOC=___(2)∠AOC=∠COD-__(3)∠AOC=∠AOB-__(4)∠AOC=∠BOD- __ -__(5)∠BOD=∠BOC+__+__(6)∠BOD=∠COD+∠AOB-__(7)∠COD=∠BOD-∠AOB+__
∠AOC ∠AOD
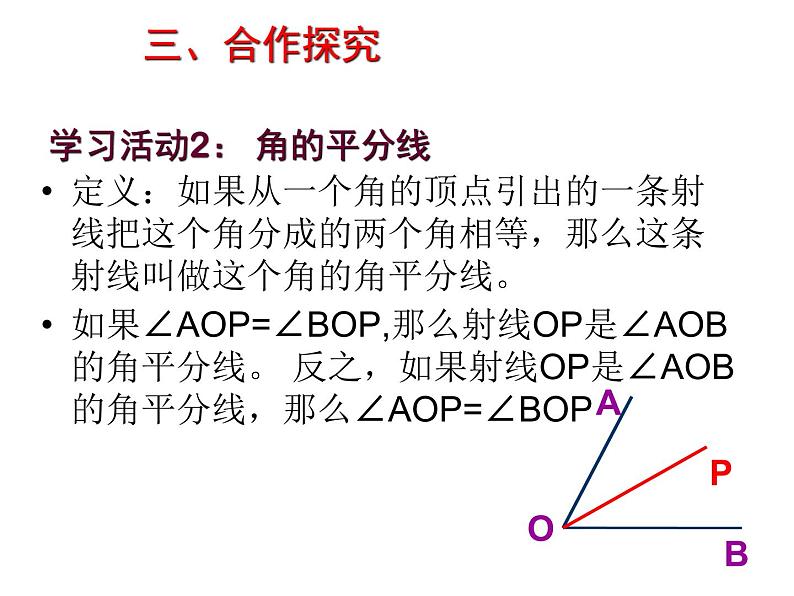
定义:如果从一个角的顶点引出的一条射线把这个角分成的两个角相等,那么这条射线叫做这个角的角平分线。如果∠AOP=∠BOP,那么射线OP是∠AOB的角平分线。 反之,如果射线OP是∠AOB的角平分线,那么∠AOP=∠BOP
学习活动2: 角的平分线
如果∠AOP=∠BOP,那么射线OP是∠AOB的角平分线。几何语言:∵∠AOP=∠BOP= ∠AOB 或∠AOB= 2∠AOP=2∠BOP ∴OP是∠AOB的角平分线
如果射线OP是∠AOB的角平分线,那么∠AOP=∠BOP几何语言:∵OP是∠AOB的角平分线∴∠AOP=∠BOP= ∠AOB 或∠AOB= 2∠AOP=2∠BOP
∵OP是∠AOB的角平分线 ∴∠AOP=∠BOP= ∠AOB 又∵∠AOB= 82° ∴∠AOP= ∠AOB = ×82° =41°
如图,如果∠AOB= 82°,OP是∠AOB的平分线,求∠AOP的度数。
如图,如果∠AOP= 41°,OP是∠AOB的平分线,求∠AOB的度数。
∵OP是∠AOB的角平分线 ∴∠AOB= 2∠AOP=2∠BOP 又∵∠AOP= 41° ∴∠AOB= 2∠AOP = 2×41° =82°
如图,如果∠AOB= 82°,OP是∠AOB的平分线,OQ是∠BOP的平分线,求∠BOQ的度数。
∵OP是∠AOB的角平分线 ∴∠AOP=∠BOP = ∠AOB 又∵∠AOB= 82° ∴∠BOP= ∠AOB = ×82° =41° 又∵OQ是∠BOP的平分线 ∴∠POQ=∠BQO = ∠BOP 又∵∠BOP=41°∴∠BQO = ∠BOP = ×41° =20.5°
如图,如果∠AOB= 82°,OP是∠AOB的平分线,OQ是∠BOP的平分线,OC是∠AOP的平分线,试求∠COQ的度数。
如图,如果∠AOB= 82°,OQ是∠BOP的平分线,OC是∠AOP的平分线,试求∠COQ的度数。
如图,如果∠AOB= α,OQ是∠BOP的平分线,OC是∠AOP的平分线,求∠COQ的度数(用α表示)。
初中数学冀教版七年级上册2.7 角的和与差课堂教学ppt课件: 这是一份初中数学冀教版七年级上册2.7 角的和与差课堂教学ppt课件,共26页。PPT课件主要包含了已知∠α和∠β,∠α与∠β互余,∠α+∠β90°,∠α+∠β180°,∠AOC与∠COB,∠DSF与∠FSE,余角和补角的性质,∠1和∠2相等,所以∠1∠2,∠3∠4等内容,欢迎下载使用。
初中冀教版2.7 角的和与差教学演示ppt课件: 这是一份初中冀教版2.7 角的和与差教学演示ppt课件,共13页。PPT课件主要包含了复习旧课,线段的和与差,知识点一角的和与差,讲授新课,知识点二角的平分线,知识点三角的计算,巩固新课,性质余角的性质,性质补角的性质,梳理新知等内容,欢迎下载使用。
初中数学冀教版七年级上册2.7 角的和与差授课ppt课件: 这是一份初中数学冀教版七年级上册2.7 角的和与差授课ppt课件,共17页。













