苏科版七年级上册5.3 展开与折叠背景图课件ppt

这是一份苏科版七年级上册5.3 展开与折叠背景图课件ppt，共30页。PPT课件主要包含了学习目标，活动一折几何体，归纳总结，连一连，说一说，想一想，V+F-E2，合作探究，试一试，综合应用等内容，欢迎下载使用。
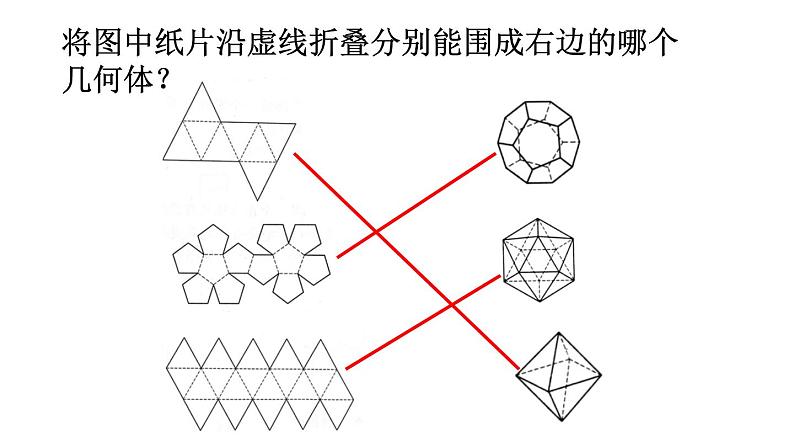
将图中纸片沿虚线折叠分别能围成右边的哪个几何体？
1、感受平面图形与立体图形之间的关系，能 根据表面展开图判断、制作简单几何体．2、感受正方体表面展开图中各个面之间的关系，会确定正方体的对应面．3、初步建立空间观念，发展几何直觉、空间想象能力和空间推理能力.
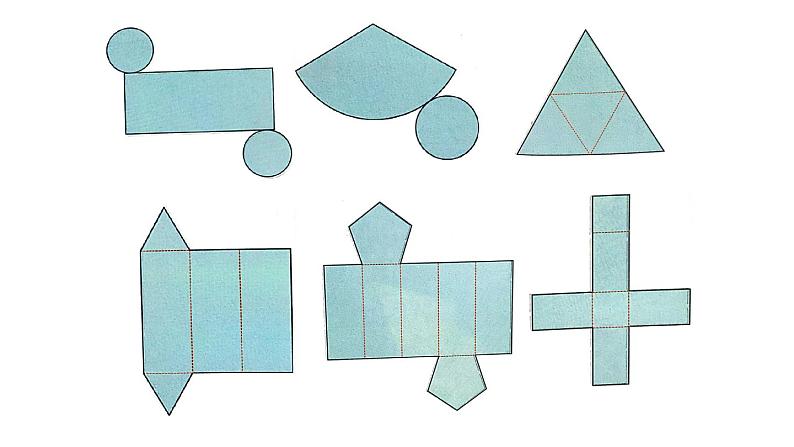
请拿出《数学实验手册》附录2、3中的纸片: 1、先想一想它们分别能围成什么几何体，再折一折验证你的猜想. 2、想一想：平面图形的形状与其所围成的几何体之间有何联系？
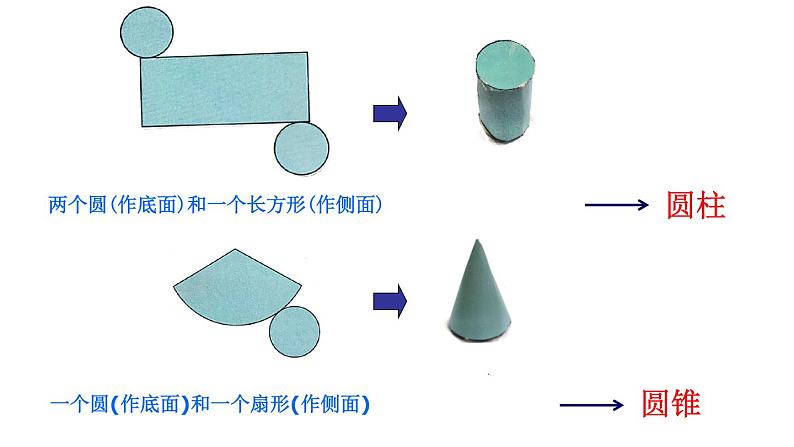
　　两个圆(作底面)和一个长方形(作侧面)
　一个圆(作底面)和一个扇形(作侧面) 　
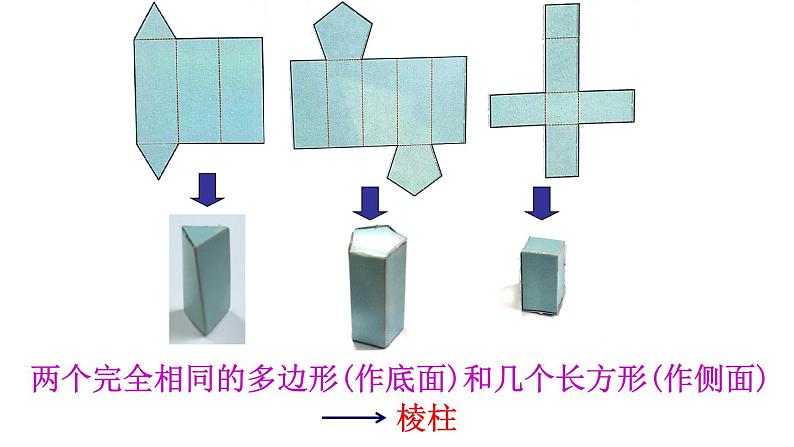
两个完全相同的多边形(作底面)和几个长方形(作侧面)
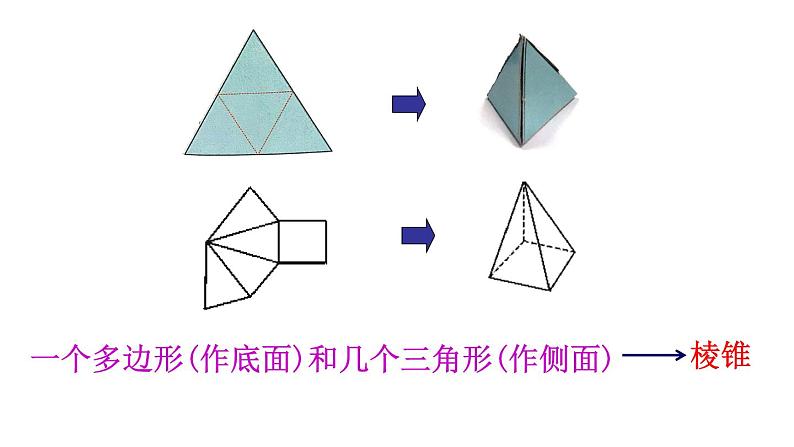
一个多边形(作底面)和几个三角形(作侧面)
将上面的平面图形与能围成的几何体连起来
说出下列平面图形能折叠成的几何体的名称.
下面图形经过折叠能否围成棱柱？
(4)可以折成棱柱．
(1)、(2)的侧面数≠底面边数(4条)，不能围成棱柱．
(3)两底面在侧面展开图的同一端,不在两端,所以不能围成棱柱．
一个几体何的面数、顶点数和棱数有何数量关系？
欧拉瑞士数学家、自然科学家.13岁时入读巴塞尔大学，15岁大学毕业，16岁获得硕士学位。 欧拉是数学史上公认的最伟大的四个最伟大的数学家之一。他是数学史上最多产的数学家，平均每年写出八百多页的论文，还写了大量的力学、分析学、几何学、变分法等的课本，《无穷小分析引论》、《微分学原理》、《积分学原理》等都成为数学界中的经典著作。 欧拉在28岁时不幸右眼失明了，人生最后7年，欧拉的双目完全失明，但他凭着记忆和心算进行研究，以惊人的速度产出了生平一半的著作直到逝世。
活动二：折正方体（1）
请拿出《数学实验手册》附录7中的纸片：先确定正方体上下左右前后再折叠，验证你的猜想.
在展开图中怎样判定正方体的对面？
“目”、“Z”两头是对面
1、下面是正方体的表面展开图（每个面都标有字），“我”、“州”的对面各是哪个面吗？
2、右边哪个平面图形能折成左边的正方体？
活动三：折正方体（2）
请拿出《数学实验手册》附录6中的纸片，先想一想它们能折成正方体吗？再折一折验证你的猜想.
含田、凹、大L不能折成正方体
如图，纸板上有10个无阴影的小正方形，哪些小正方形能与图中5个有阴影的小正方形折叠成一个正方体纸盒.（课本131页做一做4）
1、将下列平面图形折成一个正方体，想一想，它与右边的哪个图形对应？
　　2、如图，这是一个正方体的展开图，如果将它组成原来的正方体，哪些点与点C重合？
现有如图所示的废铁皮，准备用它来加工一些棱长为10 cm的无盖正方体铁盒，问怎样下料(画线)，才能使得加工的盒子最多？最多是几个？
逻辑思维、空间想象、动手操作综合应用
这节课你最大的收获是什么?
必做：教材132-133页习题5.3中第3、4、5、6题.选做：
为什么立方体的展开图只有11种？（以小组为单位讨论并说明理由）