人教A版 (2019)必修第二册8.1 基本立体图形第1课时学案

展开

这是一份人教A版 (2019)必修第二册8.1 基本立体图形第1课时学案，共11页。

1．空间几何体
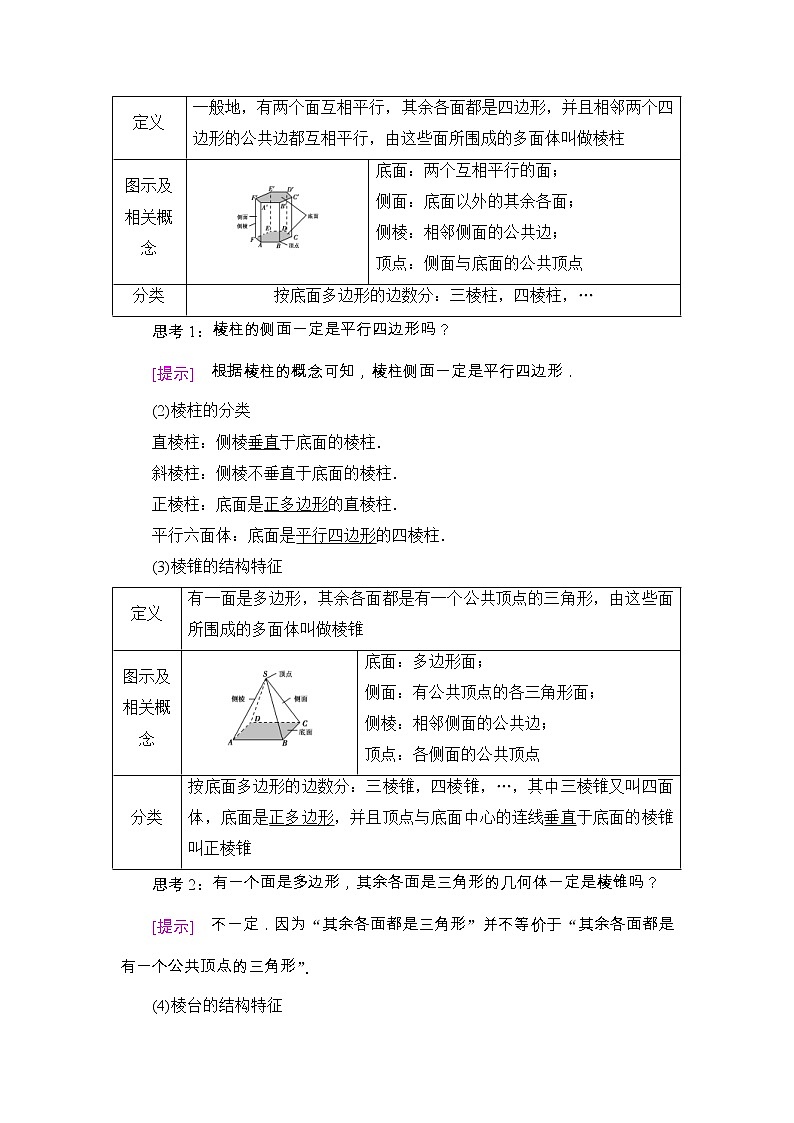
2.棱柱、棱锥、棱台的结构特征
(1)棱柱的结构特征
思考1：棱柱的侧面一定是平行四边形吗？
[提示] 根据棱柱的概念可知，棱柱侧面一定是平行四边形．
(2)棱柱的分类
直棱柱：侧棱垂直于底面的棱柱．
斜棱柱：侧棱不垂直于底面的棱柱．
正棱柱：底面是正多边形的直棱柱．
平行六面体：底面是平行四边形的四棱柱．
(3)棱锥的结构特征
思考2：有一个面是多边形，其余各面是三角形的几何体一定是棱锥吗？
[提示] 不一定．因为“其余各面都是三角形”并不等价于“其余各面都是有一个公共顶点的三角形”．
(4)棱台的结构特征
思考3：棱台的上下底面互相平行，各侧棱延长线一定相交于一点吗？
[提示] 根据棱台的定义可知其侧棱延长线一定交于一点．
1．在三棱锥ABCD中，可以当作棱锥底面的三角形的个数为( )
A．1个 B．2个 C．3个 D．4个
D [每个三角形都可以作为底面．]
2．下面说法中，正确的是( )
A．上下两个底面平行且是相似的四边形的几何体是四棱台
B．棱台的所有侧面都是梯形
C．棱台的侧棱长必相等
D．棱台的上下底面可能不是相似图形
B [由棱台的结构特点可知，A、C、D不正确．故B正确．]
3．下面属于多面体的是 (填序号)．
①建筑用的方砖；②埃及的金字塔；③茶杯；④球．
①② [①②属于多面体，③④属于旋转体．]
【例1】 (1)下列命题中，正确的是( )
A．有两个面互相平行，其余各面都是四边形的几何体叫棱柱
B．棱柱中互相平行的两个面叫做棱柱的底面
C．棱柱的侧面是平行四边形，但底面不是平行四边形
D．棱柱的侧棱都相等，侧面是平行四边形
(2)如图所示，长方体ABCDA1B1C1D1.
①这个长方体是棱柱吗？如果是，是几棱柱？为什么？
②用平面BCNM把这个长方体分成两部分，各部分形成的几何体还是棱柱吗？若是，请指出它们的底面．
(1)D [由棱柱的定义可知，只有D正确，分别构造图形如下：
① ② ③
图①中平面ABCD与平面A1B1C1D1平行，但四边形ABCD与A1B1C1D1不全等，故A错；图②中正六棱柱的相对侧面ABB1A1与EDD1E1平行，但不是底面，B错；图③中直四棱柱底面ABCD是平行四边形，C错，故选D.]
(2)[解] ①长方体是四棱柱．因为它有两个平行的平面ABCD与平面A1B1C1D1，其余各面都是四边形，并且每相邻两个四边形的公共边互相平行，这符合棱柱的定义．
②用平面BCNM把这个长方体分成两部分，其中一部分，有两个平行的平面BB1M与平面CC1N，其余各面都是四边形，并且每相邻两个四边形的公共边互相平行，这符合棱柱的定义，所以是三棱柱，可用符号表示为三棱柱BB1MCC1N.同理，另一部分也是棱柱，可以用符号表示为四棱柱ABMA1DCND1.
有关棱柱结构特征问题的解题策略：
(1)有关棱柱概念辨析问题应紧扣棱柱定义：
①两个面互相平行；
②其余各面是四边形；
③相邻两个四边形的公共边互相平行．求解时，首先看是否有两个面平行，再看是否满足其他特征．
(2)多注意观察一些实物模型和图片便于反例排除．
1．下列关于棱柱的说法错误的是( )
A．所有棱柱的两个底面都平行
B．所有的棱柱一定有两个面互相平行，其余每相邻面的公共边互相平行
C．有两个面互相平行，其余各面都是四边形的几何体一定是棱柱
D．棱柱至少有五个面
C [对于A、B、D，显然是正确的；对于C，棱柱的定义是这样的：有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面围成的几何体叫做棱柱，显然题中漏掉了“并且每相邻两个四边形的公共边都互相平行”这一条件，因此所围成的几何体不一定是棱柱．如图所示的几何体就不是棱柱，所以C错误．]
【例2】 (1)下列关于棱锥、棱台的说法：
①棱台的侧面一定不会是平行四边形；
②棱锥的侧面只能是三角形；
③由四个面围成的封闭图形只能是三棱锥；
④棱锥被平面截成的两部分不可能都是棱锥．
其中正确说法的序号是．
(2)判断如图所示的几何体是不是棱台，为什么？
(1)①②③ [①正确，棱台的侧面一定是梯形，而不是平行四边形；②正确，由棱锥的定义知棱锥的侧面只能是三角形；③正确，由四个面围成的封闭图形只能是三棱锥；④错误，如图所示，四棱锥被平面截成的两部分都是棱锥．]
(2)[解] ①②③都不是棱台．因为①和③都不是由棱锥所截得的，故①③都不是棱台，虽然②是由棱锥所截得的，但截面不和底面平行，故不是棱台，只有用平行于棱锥底面的平面去截棱锥，底面与截面之间的部分才是棱台．
关于棱锥、棱台结构特征题目的判断方法：
(1)举反例法
结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确．
(2)直接法
2．如图所示，观察以下四个几何体，其中判断正确的是 ( )
A．①是棱台 B．②是圆台
C．③是棱锥 D．④不是棱柱
C [图①中的几何体不是由棱锥截来的，且上、下底面不是相似的图形，所以①不是棱台；图②中的几何体上、下两个面不平行，所以②不是圆台；图③中的几何体是棱锥．图④中的几何体前、后两个面平行，其他面是平行四边形，且每相邻两个平行四边形的公共边平行，所以④是棱柱．故选C.]
[探究问题]
1．棱柱的侧面展开图是什么图形？正方体的表面展开图又是怎样的？
[提示] 棱柱的侧面展开图是平行四边形；正方体的表面展开图如图：
2．棱台的侧面展开图又是什么样的？
[提示] 棱台的侧面展开图是多个相连的梯形．
【例3】 (1)某同学制作了一个对面图案均相同的正方体礼品盒，如图所示，则这个正方体礼品盒的平面展开图应该为(对面是相同的图案)( )
(2)如图是三个几何体的平面展开图，请问各是什么几何体？
[思路探究] (1)正方体的平面展开图⇒以其中一个面不动把其他面展开．
(2)常见几何体的定义与结构特征⇒空间想象或动手制作平面展开图进行实践．
(1)A [由选项验证可知选A.]
(2)[解] 图①中，有5个平行四边形，而且还有两个全等的五边形，符合棱柱特点；图②中，有5个三角形，且具有共同的顶点，还有一个五边形，符合棱锥特点；图③中，有3个梯形，且其腰的延长线交于一点，还有两个相似的三角形，符合棱台的特点．把平面展开图还原为原几何体，如图所示：所以①为五棱柱，②为五棱锥，③为三棱台．
1.将本例(1)中改为：水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示，如图是一个正方体的平面展开图(图中数字写在正方体的外表面上)，若图中“0”上方的“2”在正方体的上面，则这个正方体的下面是 ( )
A．1 B．6 C．快 D．乐
B [将图形折成正方体知选B.]
2．将本例(2)的条件改为：一个几何体的平面展开图如图所示．
(1)该几何体是哪种几何体？
(2)该几何体中与“祝”字面相对的是哪个面？“你”字面相对的是哪个面？
[解] (1)该几何体是四棱台．
(2)与“祝”相对的面是“前”，与“你”相对的面是“程”．
多面体展开图问题的解题策略
(1)绘制展开图：绘制多面体的表面展开图要结合多面体的几何特征，发挥空间想象能力或者是亲手制作多面体模型．在解题过程中，常常给多面体的顶点标上字母，先把多面体的底面画出来，然后依次画出各侧面，便可得到其表面展开图．
(2)由展开图复原几何体：若是给出多面体的表面展开图，来判断是由哪一个多面体展开的，则可把上述过程逆推．同一个几何体的表面展开图可能是不一样的，也就是说，一个多面体可有多个表面展开图．
1．在理解的基础上，要牢记棱柱、棱锥、棱台的定义，能够根据定义判断几何体的形状．
2．棱柱、棱台、棱锥关系图
1．判断正误
(1)棱柱的侧面都是平行四边形．( )
(2)有一个面是多边形，其余各面都是三角形的几何体叫棱锥．( )
(3)用一平面去截棱锥底面和截面之间的部分叫棱台．( )
[答案] (1)√ (2)× (3)×
2．有一个多面体，共有四个面围成，每一个面都是三角形，则这个几何体为( )
A．四棱柱 B．四棱锥
C．三棱柱 D．三棱锥
D [根据棱锥的定义可知该几何体是三棱锥．]
3．下列图形经过折叠可以围成一个棱柱的是( )
A B C D
D [A，B，C中底面多边形的边数与侧面数不相等．]
4．一个棱柱至少有个面，顶点最少的一个棱台有条侧棱．
5 3 [面最少的棱柱是三棱柱，它有5个面；顶点最少的一个棱台是三棱台，它有3条侧棱．]
5．画一个三棱台，再把它分成：
(1)一个三棱柱和另一个多面体；
(2)三个三棱锥，并用字母表示．
[解] 画三棱台一定要利用三棱锥．
(1)如图①所示，三棱柱是棱柱A′B′C′AB″C″，另一个多面体是B′C′CBB″C″.
(2)如图②所示，三个三棱锥分别是A′ABC，
B′A′BC，C′A′B′C.
① ②
学习目标
核心素养
1.通过对实物模型的观察，归纳认知棱柱、棱锥、棱台的结构特征．(重点)
2．理解棱柱、棱锥、棱台之间的关系．(难点)
3．能运用棱柱、棱锥、棱台的结构特征描述现实生活中简单物体的结构和有关计算．(易混点)
通过空间几何体概念的学习，培养直观想象、逻辑推理的核心素养.
类别
多面体
旋转体
定义
一般地，由若干个平面多边形围成的几何体
一条平面曲线(包括直线)绕它所在平面内的一条定直线旋转所形成的曲面叫做旋转面，封闭的旋转面围成的几何体叫做旋转体
图形
定义
一般地，有两个面互相平行，其余各面都是四边形，并且相邻两个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱
图示及相关概念
底面：两个互相平行的面；
侧面：底面以外的其余各面；
侧棱：相邻侧面的公共边；
顶点：侧面与底面的公共顶点
分类
按底面多边形的边数分：三棱柱，四棱柱，…
定义
有一面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的多面体叫做棱锥
图示及相关概念
底面：多边形面；
侧面：有公共顶点的各三角形面；
侧棱：相邻侧面的公共边；
顶点：各侧面的公共顶点
分类
按底面多边形的边数分：三棱锥，四棱锥，…，其中三棱锥又叫四面体，底面是正多边形，并且顶点与底面中心的连线垂直于底面的棱锥叫正棱锥
定义
用一个平行于棱锥底面的平面去截棱锥，底面和截面之间的部分叫做棱台
图示及相关概念
上底面：原棱锥的截面；
下底面：原棱锥的底面；
侧面：除上下底面以外的面；
侧棱：相邻侧面的公共边；
顶点：侧面与上(下)底面的公共顶点
分类
由几棱锥截得，如三棱台、四棱台、…
棱柱的结构特征
棱锥、棱台的结构特征
棱锥
棱台
定底面
只有一个面是多边形，此面即为底面
两个互相平行的面，即为底面
看侧棱
相交于一点
延长后相交于一点
多面体的表面展开图