2021学年第六章 平面向量及其应用6.2 平面向量的运算导学案及答案

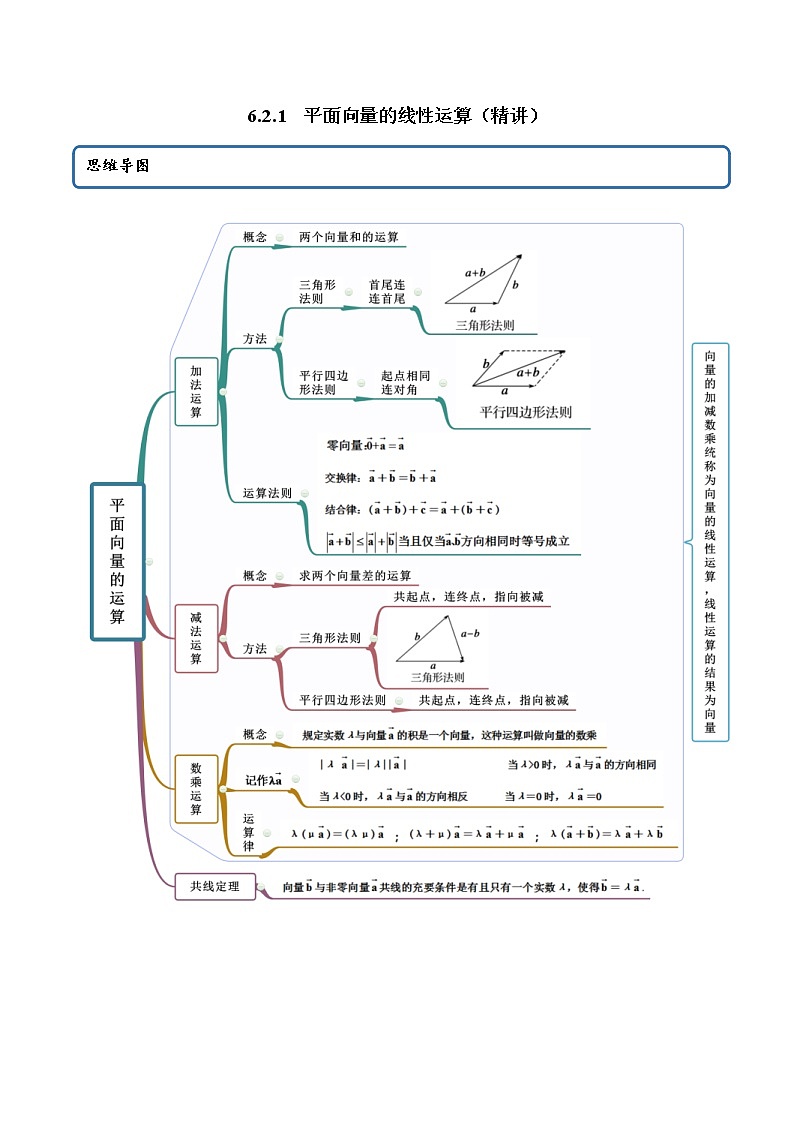
6.2.1  平面向量的线性运算（精讲）

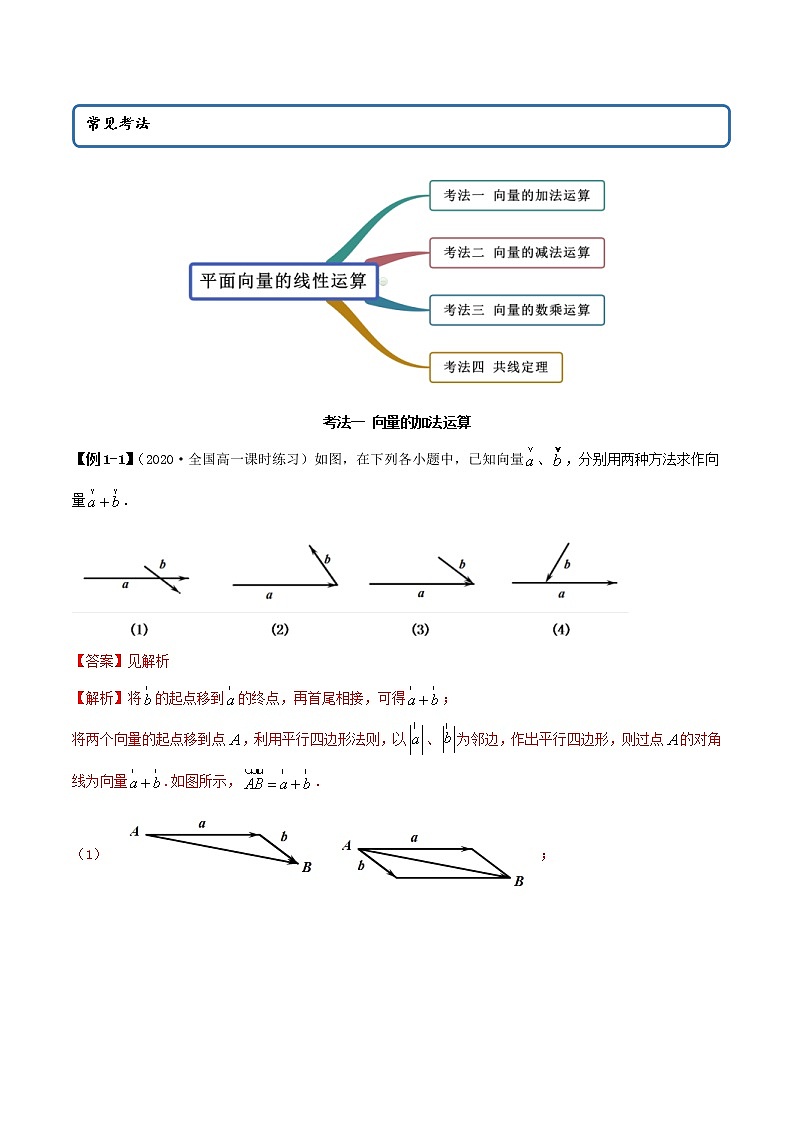
考法一 向量的加法运算

【例1-1】（2020·全国高一课时练习）如图，在下列各小题中，已知向量、，分别用两种方法求作向量．

【答案】见解析

【解析】将的起点移到的终点，再首尾相接，可得；

将两个向量的起点移到点，利用平行四边形法则，以、为邻边，作出平行四边形，则过点的对角线为向量.如图所示，．

（1）；

（2）；

（3） ；

（4）.

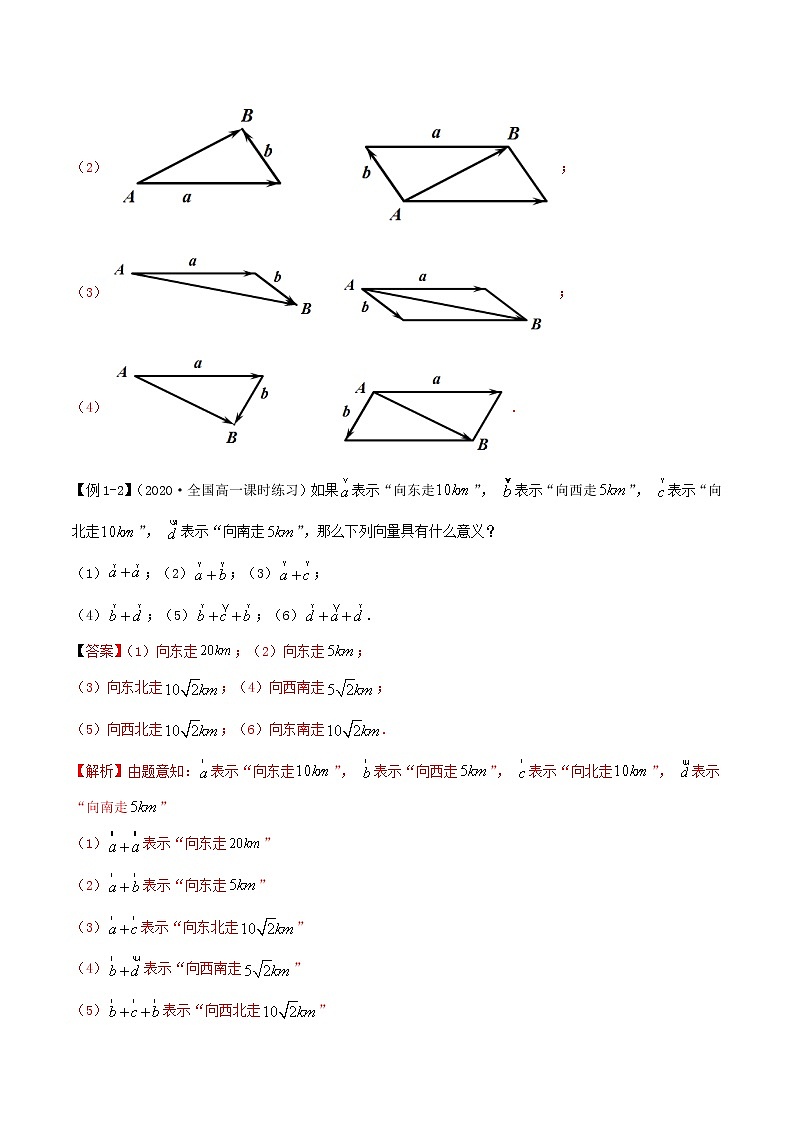
【例1-2】（2020·全国高一课时练习）如果表示“向东走”， 表示“向西走”， 表示“向北走”， 表示“向南走”，那么下列向量具有什么意义？

（1）；（2）；（3）；

（4）；（5）；（6）.

【答案】（1）向东走；（2）向东走；

（3）向东北走；（4）向西南走；

（5）向西北走；（6）向东南走.

【解析】由题意知：表示“向东走”， 表示“向西走”， 表示“向北走”， 表示“向南走”

（1）表示“向东走”

（2）表示“向东走”

（3）表示“向东北走”

（4）表示“向西南走”

（5）表示“向西北走”

（6）表示“向东南走”

【例1-3】（2021·重庆市大学城）向量﹒化简后等于（ ）

A. B.0 C. D.

【答案】D

【解析】

, 故选D.

【例1-4】（2020·湖南长沙市·高一期末）已知点D，E，F分别是△ABC各边的中点，则下列等式中错误的（    ）

A． B．

C． D．

【答案】D

【解析】由题意，根据向量的加法运算法则，可得，故A正确；

由，故B正确；

根据平行四边形法则，可得，故C正确，D不正确.故选：D.

【一隅三反】

1.如图，已知向量a，b，c，求作和向量a＋b＋c.

【答案】见解析

【解析】　方法一　可先作a＋c，再作(a＋c)＋b，即a＋b＋c.如图①，首先在平面内任取一点O，作向量＝a，接着作向量＝c，则得向量＝a＋c，然后作向量＝b，则向量＝a＋b＋c为所求．

　　　　　　①　　　　　　　　　　②

方法二　三个向量不共线，用平行四边形法则来作．如图②，

(1)在平面内任取一点O，作＝a，＝b；

(2)作平行四边形AOBC，则＝a＋b；

(3)再作向量＝c；

(4)作平行四边形CODE，则＝＋c＝a＋b＋c.即即为所求.

2．（2020·北京高二学业考试）在平行四边形中，等于（    ）

A． B． C． D．

【答案】A

【解析】根据向量加法的平行四边形法则可得，故选：A.

3．（多选）（2020·全国高一）如图，在平行四边形中，下列计算正确的是（    ）

A． B．

C． D．

【答案】ACD

【解析】由向量加法的平行四边形法则可知，故A正确；

，故B不正确；

，故C正确；

，故D正确.故选：ACD.

4.化简(1)＋；       (2)＋＋；    (3)＋＋＋＋.

(4)＋＋；   (5)(＋)＋＋.

【答案】（1）（2）（3）（4）（5）

【解析】　(1)＋＝＋＝.

(2)＋＋＝＋＋＝＋＝.

(3)＋＋＋＋＝＋＋＋＋＝＋＋＋＝＋＋＝＋＝0.

(4)＋＋＝＋＋＝＋＝0.

(5)方法一　(＋)＋＋＝(＋)＋(＋)＝＋＝.

方法二　(＋)＋＋＝＋(＋)＋＝＋＋＝＋0＝.

方法三　(＋)＋＋＝(＋＋)＋＝＋＝.

考法二 向量的减法运算

【例2-1】（2020·全国高一课时练习）如图，在各小题中，已知，分别求作．

【答案】见解析

【解析】将的起点移到同一点，再首尾相接，方向指向被减向量，

如图，，

 (1)                                  (2)

(3)                                                    (4)

【例22-2】．（2020·全国高一课时练习）化简下列各式：

①；②；③；④.

其中结果为的个数是（    ）

A．1 B．2 C．3 D．4

【答案】D

【解析】①；

②；

③；

④；

以上各式化简后结果均为,故选:D

【一隅三反】

1．（2020·全国高一课时练习）如图，已知向量，求作向量，．

【答案】见解析

【解析】如下图所示，在平面内任取一点O，

作，，，，

则，．

2.如图，已知向量a，b，c，求作向量a－b－c.

【答案】见解析

【解析】在平面内任取一点O，作向量＝a，＝b，则向量a－b＝，再作向量＝c，则向量＝a－b－c.

3．（2020·莆田第七中学高二期中）在五边形中（如图），（    ）

A． B． C． D．

【答案】B

【解析】.故选：B

4．（2020·全国高一课时练习）化简______.

【答案】

【解析】．故答案为：．

5.化简（1）(－)－(－) (2)－＋；(3)＋＋－－．

【答案】（1）  （2）（3）

【解析】（1）方法一(统一成加法)　(－)－(－)＝－－＋＝＋＋＋＝＋＋＋＝＋＝0.

方法二(利用－＝)　(－)－(－)＝－－＋＝(－)－＋＝－＋＝＋＝0.

方法三(利用＝－)　设O是平面内任意一点，则(－)－(－)＝－－＋＝(－)－(－)－(－)＋(－)＝－－＋－＋＋－＝0.

(2)－＋＝＋－＝－＝0．

(3)＋＋－－＝＋＋＋＋＝(＋)＋(＋)＋D＝＋＋＝＋＋＝0＋＝．

考法三 向量的数乘的运算

【例3-1】（2020·全国高一课时练习）把下列各小题中的向量表示为实数与向量的积：

（1），；

（2），；

（3），；

（4），．

【答案】（1）；（2）；（3）；（4）．

【解析】（1），；

（2），；

（3），；

（4），．

【例3-2】（2020·全国高一课时练习）如图，是以向量为边的平行四边形，又，试用表示．

【答案】，，

【解析】

【一隅三反】

1．（2020·全国高一课时练习）计算：

（1）；

（2）；

（3）．

【答案】（1）；（2）；（3）.

【解析】（1）原式；

（2）原式；

（3）原式．

2．（2020·全国高一课时练习）化简：

（1）；

（2）；

（3）；

（4）.

【答案】（1）；（2）；（3）；（4）

【解析】（1）.

（2）.

（3）.

（4）.

3．（2020·全国高一课时练习）如图，解答下列各题：

（1）用表示；

（2）用表示；

（3）用表示；

（4）用表示．

【答案】（1）．（2）．（3）．（4）．

【解析】由题意知，，，，，，则

（1）．

（2）．

（3）．

（4）．

考法四 向量的共线定理

【例4-1】（2020·全国高一课时练习）判断向量是否共线(其中,是两个非零不共线的向量):

(1);

(2);

(3).

【答案】(1)共线，(2)共线，(3)不共线.

【解析】(1)∵,∴,∴共线.

(2)∵,∴,∴共线.

(3)假设,则,∴.

∵不共线,∴此方程组无解.∴不存在实数,使得,∴不共线.

【例4-2】（2020·全国高一课时练习）(1)已知向量不共线,若,,,试证:三点共线.

(2)设是两个不共线向量,已知,,,若三点共线,求k的值.

【答案】(1)见解析(2)-8

【解析】(1)，，

，与共线.

又与有公共点B，三点共线.

(2).

三点共线，共线.

∴存在实数使，即.

.

与不共线，.

【一隅三反】

1．（2020·全国高一课时练习）判断下列各小题中的向量,是否共线（其中是两个非零不共线向量）．

（1）；

（2）；

（3）．

【答案】(1) 与共线；(2) 与共线；(3) 与不共线．

【解析】（1）∵，∴与共线．

（2）∵，∴与共线．

（3）设，则，∴．

∵与是两个非零不共线向量，∴，．

这样的不存在，∴与不共线．

2．（2020·新泰市第二中学高一期中）设是不共线的两个非零向量.

（1）若，求证：三点共线；

（2）若与共线，求实数的值；

（3）若，且三点共线，求实数的值.

【答案】（1）证明见解析；（2）.（3）.

【解析】证明：（1），所以.

又因为为公共点，所以三点共线.

（2）设，则

解得或

所以实数的值为.

（3），

因为三点共线，所以与共线.

从而存在实数使，即，

得解得所以.

3．（2020·洛阳市）为内一点，且，，若，，三点共线，则的值为（ ）

A． B． C． D．

【答案】A

【解析】由有,所以,因为，，三点共线,所以,则,故有,,选A.