

人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直学案设计
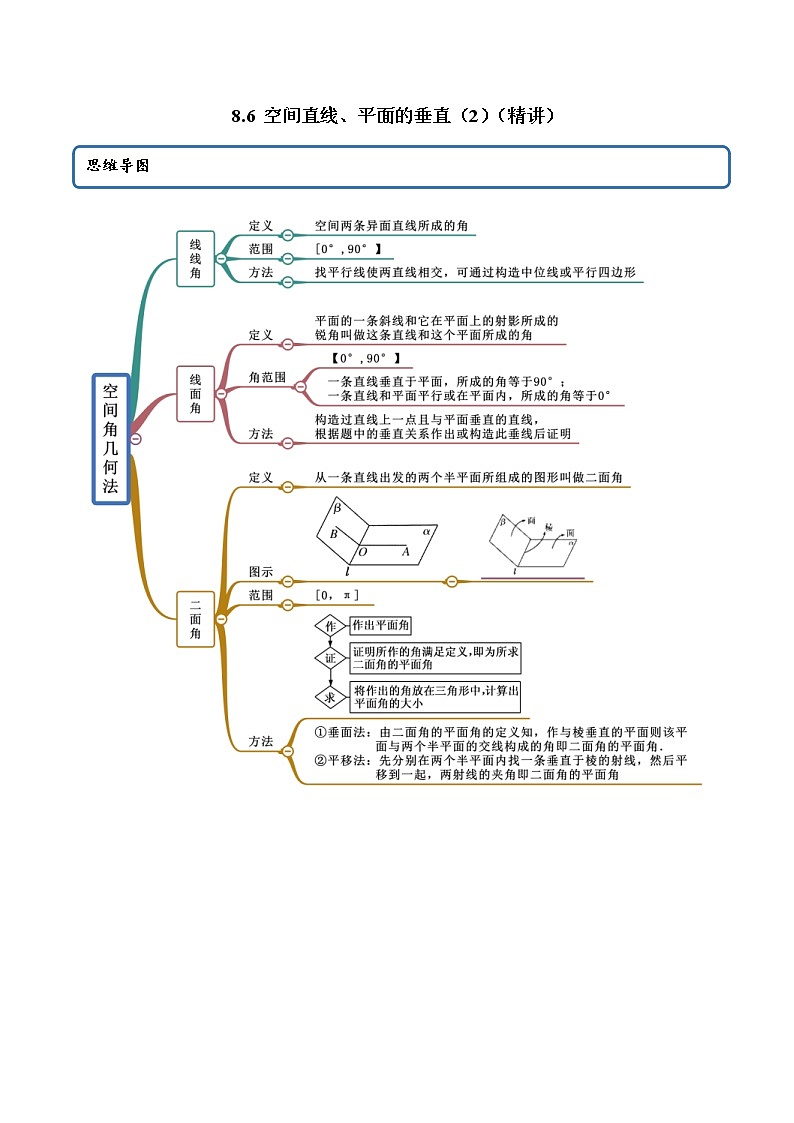
展开8.6 空间直线、平面的垂直(2)(精讲)
考法一 线线角
【例1】(2021·广西河池市·高一期末)如图,在四棱锥中,平面,四边形为正方形,,为的中点,则异面直线与所成的角的正弦值为( ).
A. B. C. D.
【答案】D
【解析】连,相交于点,连、,
因为为的中点,为的中点,有,可得为异面直线与所成的角,不妨设正方形中,,则,
由平面,可得,
则,,
因为,为的中点,所以,.
故选:D.
【一隅三反】
1.(2021·浙江高一期末)在正方体中,是正方形的中心,则直线与直线所成角大小为( )
A.30° B.45° C.60° D.90°
【答案】A
【解析】设正方体的棱长为,连接,,,
因为,故或其补角为直线与直线所成角.
而,,,
故,所以,
所以,因为为锐角,故,
故选:A.
2.(2021·西安市航天城第一中学高一期末)在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )
A. B.- C.2 D.
【答案】A
【解析】如图所示,
分别取,,,的中点,,,,则,,,
或其补角为异面直线与所成角.
设,则,,
,
异面直线与所成角的余弦值为,
故选:A.
3.(2021·陕西西安市·西安中学高一期末)如图,四面体中,,,E,F分别是的中点,若,则与所成的角的大小是( )
A. B. C. D.
【答案】A
【解析】如图所示:
取BC的中点G,连接EG,FG,
因为E,F,G都为中点,所以,
所以,分别为异面直线EF与AB,EF与CD所成的角,
因为,所以
又因为,,所以 所以,
因为,所以故选:A
考法二 线面角
【例2】(2021·河南高一期末)在三棱柱中,,,且,则直线与平面所成的角的大小为( )
A.30° B.45° C.60° D.90°
【答案】A
【解析】∵,,∴,
∵,,,平面,
∴平面,
∴就是与平面所成的角,即与平面所成的角是,
∵棱柱中,∴与平面所成的角的大小为,
故选:A.
【一隅三反】
1.(2021·全国高一课时练习)直三棱柱中,,,则与面成角的正弦值为( )
A. B. C. D.
【答案】A
【解析】如图,过作,连接,
在直三棱柱中,因为
所以平面,
故在平面上的射影为,
所以为直线与平面所成的角,
设,又
所以
故故选:A
2.(2021·浙江高一期末)如图,已知平面,平面,为等边三角形,,F为的中点.
(Ⅰ)求证:平面;
(Ⅱ)求直线和平面所成角的正弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)
【解析】(Ⅰ)取CE中点G,连接BG,FG,如图所示:
因为F、G分别为CD、CE的中点,
所以且,
又因为平面,平面,
所以,,
所以,,
所以四边形ABGF为平行四边形,
所以,
又因为平面,平面,
所以平面;
(Ⅱ)因为平面,平面ACD,
所以,所以,
又为等边三角形,F为CD的中点,
所以,
又平面CDE,
所以平面CDE,即平面CDE,
又平面CDE,则,
连接DG,BD,如图所示,
则即为直线和平面所成角,
设,在中,,
在直角梯形ABED中,,
在中,,
所以,
所以直线和平面所成角的正弦值为.
3.(2021·河南焦作市·高一期末)如图,四棱锥的底面为正方形,底面,,,分别为,,的中点.
(1)求证:平面;
(2)若,求直线与平面所成线面角的正弦值.
【答案】(1)证明见解析;(2).
【解析】(1)因为底面,底面,
所以,因为,分别为正方形的边,的中点,
,
所以,所以,由
所以,所以,
因为平面,平面,,
所以平面.
(2)由(1)可知平面,
设,如图,连接,则即为直线与平面所成线面角,
因为,所以,,
在中,由于,所以,
所以,所以,
所以在中,,即直线与平面所成线面角的正弦值为.
考法三 面面角
【例3】(2021·全国高一课时练习)如图,三棱台的下底面是正三角形,,则二面角的大小是( )
A.30° B.45° C.60° D.90°
【答案】C
【解析】三棱台中,,且,
则,又,且,
所以平面,
所以为的二面角,
因为为等边三角形,
所以.
故选:C
【一隅三反】
1.(2021·浙江高一期末)长方体中,,,则二面角的余弦值的大小为( )
A. B. C. D.
【答案】B
【解析】
取中点,连接、,因为,,
所以,,所以即为二面角的平面角,连接,
,,所以,又因为,
在中,,
所以二面角的余弦值为,
故选:B
2.(2021·浙江高一期末)如图,已知平面.
(Ⅰ)求证:平面平面;
(Ⅱ)若,求二面角的大小.
【答案】(Ⅰ)证明见解析;(Ⅱ)
【解析】(Ⅰ)平面,平面,,
,,
平面,
平面,平面平面;
(Ⅱ)由(1)得平面,
平面,,
,即为二面角的平面角,
在直角三角形中,,则,
,即二面角的大小为.
3.(2021·陕西西安市·西安中学高一期末)如图所示,在长方体中,,点E是的中点.
(1)证明:平面;
(2)证明:;
(3)求二面角的正切值.
【答案】(1)证明见解析;(2)证明见解析;(3).
【解析】(1)如图所示:
连接交于点O,连接,则O为的中点.
∵E是的中点,∴
又平面,平面,
∴平面.
(2)由题意可知,四边形是正方形,
∴.
∵平面,平面,
∴.
∵平面,平面,,
∴平面.
又平面,
∴,即.
(3)在中,,,,
∴
∵平面平面,
∴.
∵平面,平面,,
∴平面.
又∵平面,
∴.
∴是二面角的平面角.
在A中,∵,,,
∴,∴二面角的正切值为.
高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直学案: 这是一份高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直学案,共55页。
高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直导学案及答案: 这是一份高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直导学案及答案,共4页。
人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直导学案及答案: 这是一份人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直导学案及答案,共13页。













