高中数学北师大版 (2019)必修 第二册第六章 立体几何初步6 简单几何体的再认识6.2 柱、锥、台的体积导学案

这是一份高中数学北师大版 (2019)必修 第二册第六章 立体几何初步6 简单几何体的再认识6.2 柱、锥、台的体积导学案，共7页。
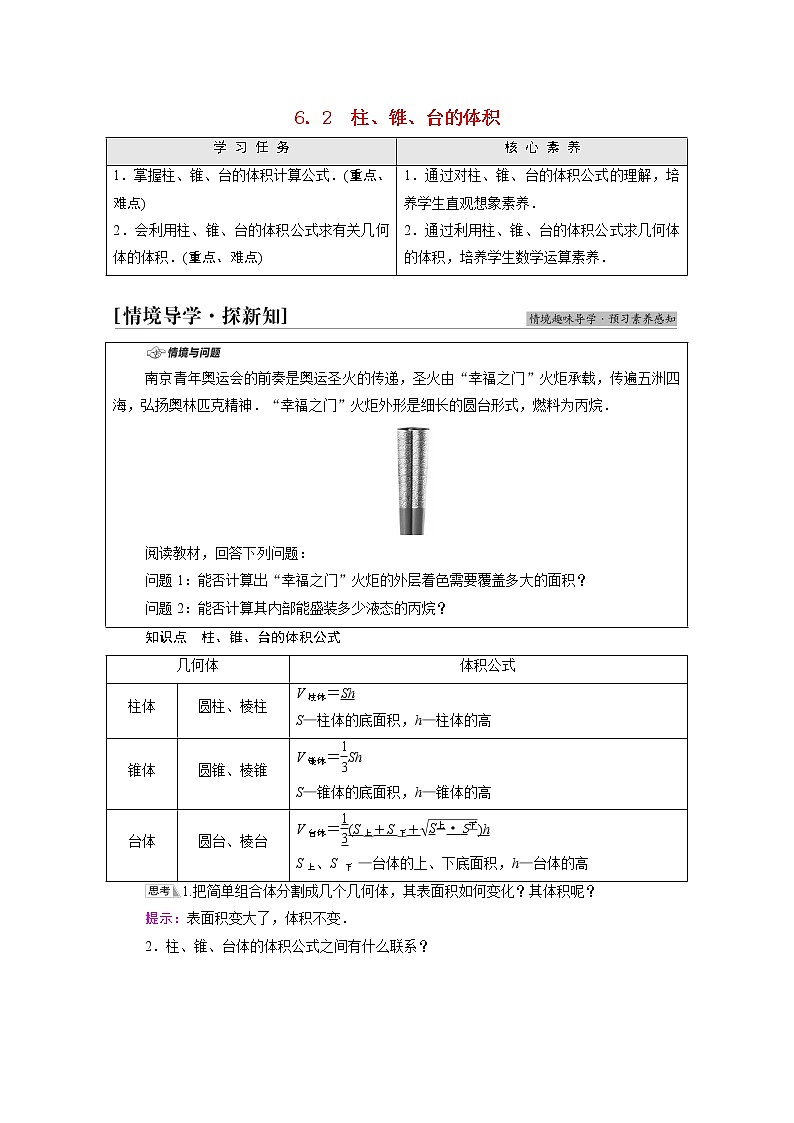
6．2　柱、锥、台的体积学 习 任 务核 心 素 养1．掌握柱、锥、台的体积计算公式．(重点、难点)2．会利用柱、锥、台的体积公式求有关几何体的体积．(重点、难点)1．通过对柱、锥、台的体积公式的理解，培养学生直观想象素养．2．通过利用柱、锥、台的体积公式求几何体的体积，培养学生数学运算素养． 南京青年奥运会的前奏是奥运圣火的传递，圣火由“幸福之门”火炬承载，传遍五洲四海，弘扬奥林匹克精神．“幸福之门”火炬外形是细长的圆台形式，燃料为丙烷．阅读教材，回答下列问题：问题1：能否计算出“幸福之门”火炬的外层着色需要覆盖多大的面积？问题2：能否计算其内部能盛装多少液态的丙烷？知识点　柱、锥、台的体积公式几何体体积公式柱体圆柱、棱柱V柱体＝ShS—柱体的底面积，h—柱体的高锥体圆锥、棱锥V锥体＝ShS—锥体的底面积，h—锥体的高台体圆台、棱台V台体＝(S上＋S下＋)hS上、S 下 —台体的上、下底面积，h—台体的高1.把简单组合体分割成几个几何体，其表面积如何变化？其体积呢？提示：表面积变大了，体积不变．2．柱、锥、台体的体积公式之间有什么联系？提示：思考辨析(正确的画“√”，错误的画“×”)(1)锥体的体积等于底面积与高之积． (　　)(2)台体的体积可转化为两个锥体的体积之差． (　　)提示：(1)错误．V锥体＝Sh，S为锥体底面积，h为锥体的高．(2)正确．[答案]　(1)×　(2)√ 类型1　多面体的体积【例1】　(教材北师版P240例4改编)如图，棱锥的底面ABCD是一个矩形，AC与BD交于点M，VM是棱锥的高．若VM＝4 cm，AB＝4 cm，VC＝5 cm，求锥体的体积．[解]　∵VM是棱锥的高，∴VM⊥MC.在Rt△VMC中，MC＝＝＝3(cm)，∴AC＝2MC＝6(cm).在Rt△ABC中，BC＝ ＝＝2(cm).S底＝AB·BC＝4×2＝8(cm2)，∴V锥＝S底h＝×8×4＝(cm3).∴棱锥的体积为cm3.(1)锥体的体积公式V＝既适合棱锥，也适合圆锥，其中棱锥可以是正棱锥，也可以不是正棱锥．(2)求柱体的体积关键是求其底面积和高，底面积利用平面图形面积的求法，常转化为三角形及四边形，高常与侧棱、斜高及其在底面的投影组成直角三角形，进而求解．1．如图是一个水平放置的正三棱柱ABC－A1B1C1，D是棱BC的中点．其中AD＝，AA1＝3，求正三棱柱ABC－A1B1C1的体积．[解]　在正三棱柱中，AD＝，AA1＝3，从而在等边三角形ABC中，AB＝＝＝2，所以正三棱柱的体积V＝Sh＝×BC×AD×AA1＝×2××3＝3. 类型2　旋转体的体积【例2】　体积为52 cm3的圆台，一个底面面积是另一个底面面积的9倍，那么截得这个圆台的圆锥的体积为(　　)A．54 cm3　 B．54π cm3C．58 cm3     D．58π cm3 A　[由底面积之比为1∶9知，体积之比为1∶27，截得小圆锥与圆台体积比为1∶26，所以小圆锥体积为2 cm3，故原来圆锥的体积为54 cm3.]旋转体体积的求法要充分利用旋转体的轴截面，将已知条件尽量归结到轴截面中求解，分析题中给出的数据，列出关系式后求出有关的量，再根据几何体的体积公式进行运算、解答．(1)求台体的体积，其关键在于求高，在圆台中，一般把高放在等腰梯形中求解．(2)“还台为锥”是求解台体的体积问题的重要思想，作出截面图，将空间问题平面化，是解决此类问题的关键．2．如果轴截面为正方形的圆柱的侧面积是4π，那么圆柱的体积等于(　　)A．π     B．2πC．4π     D．8πB　[设圆柱的底面半径为r，则圆柱的母线长为2r，由题意得S圆柱侧＝2πr×2r＝4πr2＝4π，所以r＝1，所以V圆柱＝πr2×2r＝2πr3＝2π.] 类型3　体积的综合问题【例3】　如图，已知ABCD－A1B1C1D1是棱长为a的正方体，E为AA1的中点，F为CC1上一点，求三棱锥A1－D1EF的体积．1．三棱锥A－BCD和B－ACD的底面积、高分别相等吗？体积相等吗？[提示]　棱锥A－BCD和B－ACD的底面积、高可能不分别相等，但它们的体积相等．2．由尝试与发现1可以得到什么启示？[提示]　求一个三棱锥的体积，当其底面积或高不易求出时，可通过转换其底面积和高来求其体积．3．观察可知三棱锥A1－D1EF和F－A1D1E的体积相等，但三棱锥F－A1D1E的高易求，所以可求三棱锥F－A1D1E的体积．[解]　由题可知V三棱锥A1－D1EF＝V三棱锥F－A1D1E, ∵S△A1D1E＝EA1·A1D1＝a2，又三棱锥F－A1D1E的高为CD＝a，∴V三棱锥F－A1D1E＝×a×a2＝a3，∴V三棱锥A1－D1EF＝a3.本例中条件改为点F为CC1的中点，其他条件不变，如图，求四棱锥A1－EBFD1的体积．[解]　因为EB＝BF＝FD1＝D1E＝＝a，D1F∥EB，所以四边形EBFD1是菱形．连接EF，则△EFB≌△FED1.因为三棱锥A1－EFB与三棱锥A1－FED1的高相等，所以V四棱锥A1－EBFD1＝2V三棱锥A1－EFB＝2V三棱锥F－EBA1.又因为S△EBA1＝EA1·AB＝a2，所以V三棱锥F－EBA1＝a3，所以V四棱锥A1－EBFD1＝2V三棱锥F－EBA1＝a3.求几何体体积的四种常用方法(1)公式法：规则几何体直接代入公式求解．(2)等积法：如四面体的任何一个面都可以作为底面，只需选用底面积和高都易求的形式即可．(3)补体法：将几何体补成易求解的几何体，如棱锥补成棱柱、三棱柱补成四棱柱等．(4)分割法：将几何体分割成易求解的几部分，分别求体积．3．如图，在多面体ABCDEF中，已知面ABCD是边长为4的正方形，EF∥AB，EF＝2，EF上任意一点到平面ABCD的距离均为3，求该多面体的体积．[解]　如图，连接EB，EC.四棱锥E­ABCD的体积V四棱锥E­ABCD＝×42×3＝16.∵AB＝2EF，EF∥AB，∴S△EAB＝2S△BEF.∴V三棱锥F­EBC＝V三棱锥C­EFB＝V三棱锥C­ABE＝V三棱锥E­ABC＝×V四棱锥E­ABCD＝4.∴多面体的体积V＝V四棱锥E­ABCD＋V三棱锥F­EBC＝16＋4＝20.1．已知高为3的直棱柱ABC—A1B1C1的底面是边长为1的正三角形(如图)，则三棱锥B1—ABC的体积为(　　)A．　　 B．C．     D．D　[V＝Sh＝××3＝.]2．棱台的上、下底面面积分别是2，4，高为3，则该棱台的体积是(　　)A．18＋6　 B．6＋2C．24     D．18B　[V＝(2＋4＋)×3＝6＋2.]3．如图，ABC­A′B′C′是体积为1的棱柱，则四棱锥C­AA′B′B的体积是(　　)A．     B．C．     D．C　[∵VC­A′B′C′＝VABC­A′B′C′＝，∴VC­AA′B′B＝1－＝.]4.如图，将一个长方体用过相邻三条棱的中点的平面截出一个棱锥，则该棱锥的体积与剩下的几何体体积的比为(　　)A．     B．C．     D．B　[设长方体的相邻三条棱长分别为a，b，c，它截出棱锥的体积为V1＝××a×b×c＝abc，剩下的几何体的体积V2＝abc－abc＝ abc，所以V1∶V2＝1∶47.]5．若圆锥的底面半径为3，母线长为5，则圆锥的体积是________．12π　[由已知圆锥的高h＝＝4，所以V圆锥＝π×32×4＝12π.]回顾本节内容，自我完成下面问题：求解几何体的体积时应注意哪些问题？提示：(1)求几何体的体积的难点是求出几何体的高，要善于利用线、面的位置关系求解．(2)对于棱锥体积的求解，当高不易求出时，要注意用换顶点法求解．(3)对不规则几何体的体积，要注意分割与补形．将不规则的几何体通过分割或补形将其转化为规则的几何体求解．