

高中数学北师大版 (2019)必修 第二册2.3 三角函数的叠加及其应用第1课时导学案
展开§6 平面向量的应用
6.1 余弦定理与正弦定理
第1课时 余弦定理
学 习 任 务 | 核 心 素 养 |
1.通过对特殊三角形边角间数量关系的研究,发现余弦定理,并了解其向量证法.(难点) 2.掌握余弦定理,并能解决一些简单的三角形度量问题.(重点) | 1.通过余弦定理的证明,培养逻辑推理素养. 2.通过余弦定理的应用,培养数学运算素养. |
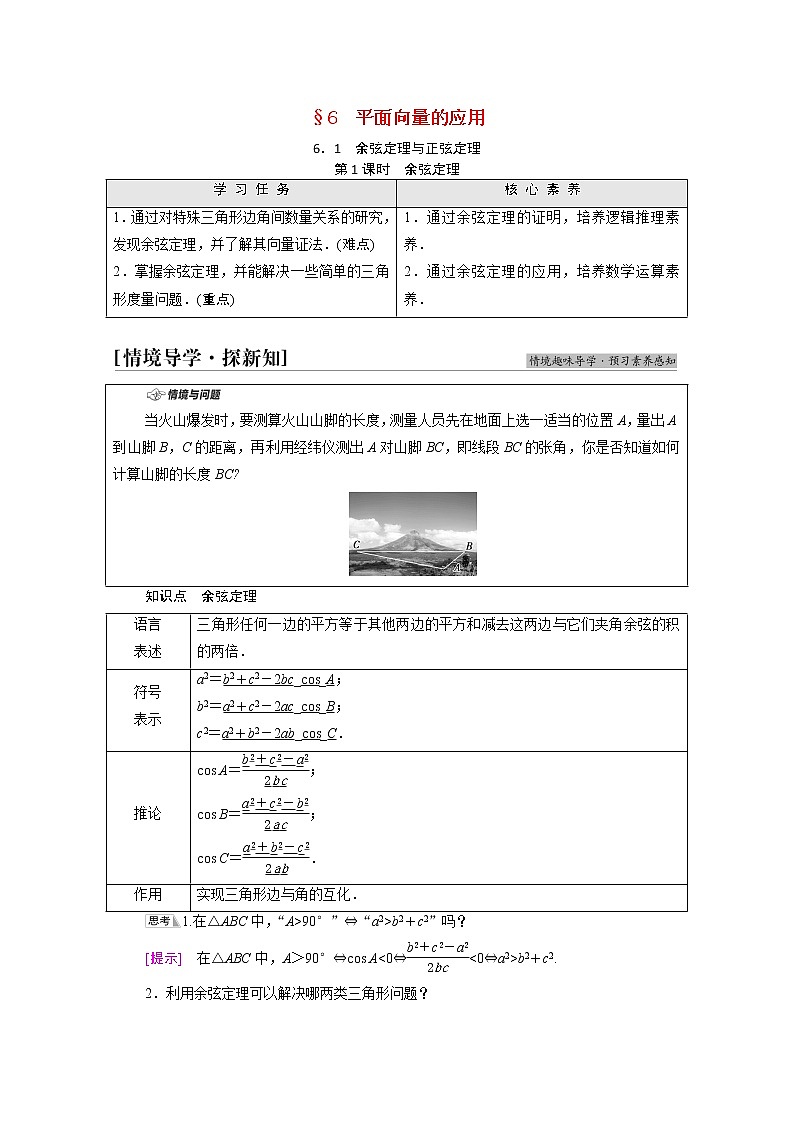
当火山爆发时,要测算火山山脚的长度,测量人员先在地面上选一适当的位置A,量出A到山脚B,C的距离,再利用经纬仪测出A对山脚BC,即线段BC的张角,你是否知道如何计算山脚的长度BC?
知识点 余弦定理
语言 表述 | 三角形任何一边的平方等于其他两边的平方和减去这两边与它们夹角余弦的积的两倍. |
符号 表示 | a2=b2+c2-2bc_cos_A; b2=a2+c2-2ac_cos_B; c2=a2+b2-2ab_cos_C. |
推论 | cos A=; cos B=; cos C=. |
作用 | 实现三角形边与角的互化. |
1.在△ABC中,“A>90°”⇔“a2>b2+c2”吗?
[提示] 在△ABC中,A>90°⇔cos A<0⇔<0⇔a2>b2+c2.
2.利用余弦定理可以解决哪两类三角形问题?
[提示] (1)已知三边,求各角;(2)已知两边和它们的夹角,求第三边和其他两角.
1.思考辨析(正确的画“√”,错误的画“×”)
(1)余弦定理揭示了任意三角形边角之间的关系,因此,它适用于任何三角形. ( )
(2)在△ABC中,若a2>b2+c2,则△ABC一定为钝角三角形.
( )
(3)在△ABC中,已知两边和其夹角时,△ABC不唯一. ( )
[答案] (1)√ (2)√ (3)×
2.在△ABC中,若a=2,b=2,c=+,则∠A的度数是( )
A.30° B.45° C. 60° D.75°
A [∵cos A==,∴A=30°.]
类型1 已知两边及一角解三角形
【例1】 (1)在△ABC中,a=1,b=2,cos C=,则c=________,cos A=________;
(2)在△ABC中,若AB=,AC=5,且cos C=,则BC=________.
(1)2 (2)4或5 [(1)根据余弦定理,得c2=a2+b2-2ab cos C=12+22-2×1×2×=4,解得c=2.
由a=1,b=2,c=2,
得cos A==.
(2)由余弦定理得:()2=52+BC2-2×5×BC×,
所以BC2-9BC+20=0,解得BC=4或BC=5.]
已知两边及—角解三角形的两种情况
(1)若已知角是其中一边的对角,可用余弦定理列出关于第三边的一元二次方程求解;
(2)若已知角是两边的夹角,则直接运用余弦定理求出另外一边,再用余弦定理和三角形内角和定理求其它角.
1.在△ABC中,角A,B,C的对边分别为a,b,c,若a=3,b=2,cos (A+B)=,则c=( )
A.4 B. C.3 D.
D [cos C=-cos (A+B)=-.又由余弦定理得c2=a2+b2-2ab cos C=9+4-2×3×2×(-)=17,所以c=.故选D.]
类型2 已知三边解三角形
【例2】 在△ABC中,a=2,b=2,c=+,求角A,B,C.
[解] cos A=
==,
∵0°<A<180°,
∴A=60°,
cos B=
==,
∵0°<B<180°,
∴B=45°,
∴C=180°-A-B=180°-60°-45°=75°.
(1)(变条件,变设问)若三角形三边长之比是1∶∶2,则其所对角之比是( )
A.1∶2∶3 B.1∶∶2
C.1∶∶ D.∶∶2
(2)(变条件)已知△ABC中,a∶b∶c=2∶∶(+1),求△ABC中各角的度数.
(1)A [设三角形三边长分别为m,m,2m(m>0),设最大角为A,
则cos A==0,
∵0°<A<180°,∴A=90°.
设最小角为B,
则cos B==,
∵0°<B<180°,∴B=30°,∴C=60°.
故三角形三角之比为1∶2∶3,故选A.]
(2)[解] 已知a∶b∶c=2∶∶(+1),令a=2k,b=k,c=(+1)k(k>0),由余弦定理的推论,得
cos A=
==,
∵0°<A<180°,∴A=45°.
cos B=
==,
∵0°<B<180°,∴B=60°.
∴C=180°-A-B=180°-45°-60°=75°.
已知三角形三边解三角形的方法
先利用余弦定理的推论求出一个角的余弦,从而求出第一个角;再利用余弦定理的推论求出第二个角;最后利用三角形的内角和定理求出第三个角.
2.在△ABC中,若a=+1,b=-1,c=,则△ABC的最大角的度数为( )
A.60° B.90° C.120° D.150°
C [∵c>a>b,∴C是最大角,
由余弦定理得,cos C===-.∴C=120°.]
类型3 余弦定理的综合应用
【例3】 (1)在△ABC中,若a cos A+b cos B=c cos C,则△ABC的形状为________;
(2)在△ABC中,已知A=,a,b,c分别是角A,B,C的对边.
①若mbc=b2+c2-a2,求实数m的值;
②若a=2,求△ABC面积的最大值.
(1)直角三角形 [由余弦定理可得a·+b·=c·,
等式两边同乘以2abc得
a2(b2+c2-a2)+b2(a2+c2-b2)=c2(a2+b2-c2),
整理化简得a4+b4-2a2b2=c4,即(a2-b2)2=c4.
因此有a2-b2=c2或b2-a2=c2,
即a2=b2+c2或b2=a2+c2,
故△ABC为直角三角形.]
(2)[解] ①∵mbc=b2+c2-a2,
∴=,
由余弦定理可知
cos A==,即=,
∴m=1.
②∵在△ABC中由余弦定理得
a2=b2+c2-2bc cos A,
即4=b2+c2-bc,
∴b2+c2=4+bc,
又∵b2+c2≥2bc,∴4+bc≥2bc,
∴bc≤4.
∴S△ABC=·c·h=c·b sin A=bc≤.
∴△ABC面积的最大值为.
判断三角形形状
一般有两个思路:(1)化边为角,求出三个角之间的关系;(2)化角为边,再进行代数恒等变换,求出三条边之间的关系.一般地,若遇到的式子含角的余弦或边的二次式,则要考虑用余弦定理.
3.已知钝角三角形ABC的三边a=k,b=k+2,c=k+4,求实数k的取值范围.
[解] ∵c>b>a>0,且△ABC为钝角三角形,∴C为钝角.
由余弦定理的推论得
cos C==<0.
∴k2-4k-12<0,解得-2<k<6.
由三角形的两边之和大于第三边,得k+(k+2)>k+4,∴k>2.
综上所述,实数k的取值范围为(2,6).
1.(多选题)在△ABC中不符合余弦定理的是( )
A.c2=a2+b2-2ab cos C B.c2=a2-b2-2bc cos A
C.b2=a2-c2-2bc cos A D.cos C=
BCD [由余弦定理及其推论知只有A正确.故选BCD.]
2.在△ABC中,已知a=9,b=2,C=150°,则c等于( )
A. B.8 C.10 D.7
D [由余弦定理得:
c===7.故选D.]
3.△ABC的内角A,B,C的对边分别为a,b,c,已知a=,c=2,cos A=,则b=( )
A. B. C.2 D.3
D [由余弦定理得5=b2+4-2×b×2×,解得b=3或b=-(舍去).故选D.]
4.已知a,b,c为△ABC的三边,B=120°,则a2+c2+ac-b2=________.
0 [∵b2=a2+c2-2ac cos B=a2+c2-2ac cos 120°
=a2+c2+ac,∴a2+c2+ac-b2=0.]
5.在△ABC中,若b=1,c=,C=,则a=________.
1 [由余弦定理得c2=a2+b2-2ab cos C,
∴a2+1+a=3,即a2+a-2=0,
解得a=1或a=-2(舍).]
回顾本节内容,自我完成以下问题:
1.怎样正确理解余弦定理?
[提示] 对余弦定理的理解
(1)适用范围:余弦定理对任意的三角形都成立;
(2)结构特征:“平方”“夹角”“余弦”;
(3)揭示的规律:余弦定理指的是三角形中三条边与其中一个角的余弦之间的关系,它描述了任意三角形中边与角的一种数量关系;
(4)主要功能:余弦定理的主要功能是实现三角形中边角关系的互化.
2.利用余弦定理可以解决哪几类问题?
[提示] 余弦定理揭示了三角形中的边角关系,利用余弦定理可以解决以下两类三角形问题:
(1)已知三边,求各角;
(2)已知两边和它们的夹角,求第三边和其他两角.
(3)利用余弦定理也可求解已知三角形两边和其中一边的对角解三角形的问题,建立关于第三边的方程,通过解方程求第三边.
高中数学北师大版 (2019)必修 第二册6.1 余弦定理与正弦定理第1课时导学案: 这是一份高中数学北师大版 (2019)必修 第二册6.1 余弦定理与正弦定理第1课时导学案,共7页。
2020-2021学年6.1 余弦定理与正弦定理第2课时导学案: 这是一份2020-2021学年6.1 余弦定理与正弦定理第2课时导学案,共8页。
北师大版 (2019)必修 第二册1.3 综合应用导学案及答案: 这是一份北师大版 (2019)必修 第二册1.3 综合应用导学案及答案,共4页。













