人教A版 (2019)必修 第二册9.2 用样本估计总体第1课时课堂检测

这是一份人教A版 (2019)必修 第二册9.2 用样本估计总体第1课时课堂检测，共10页。
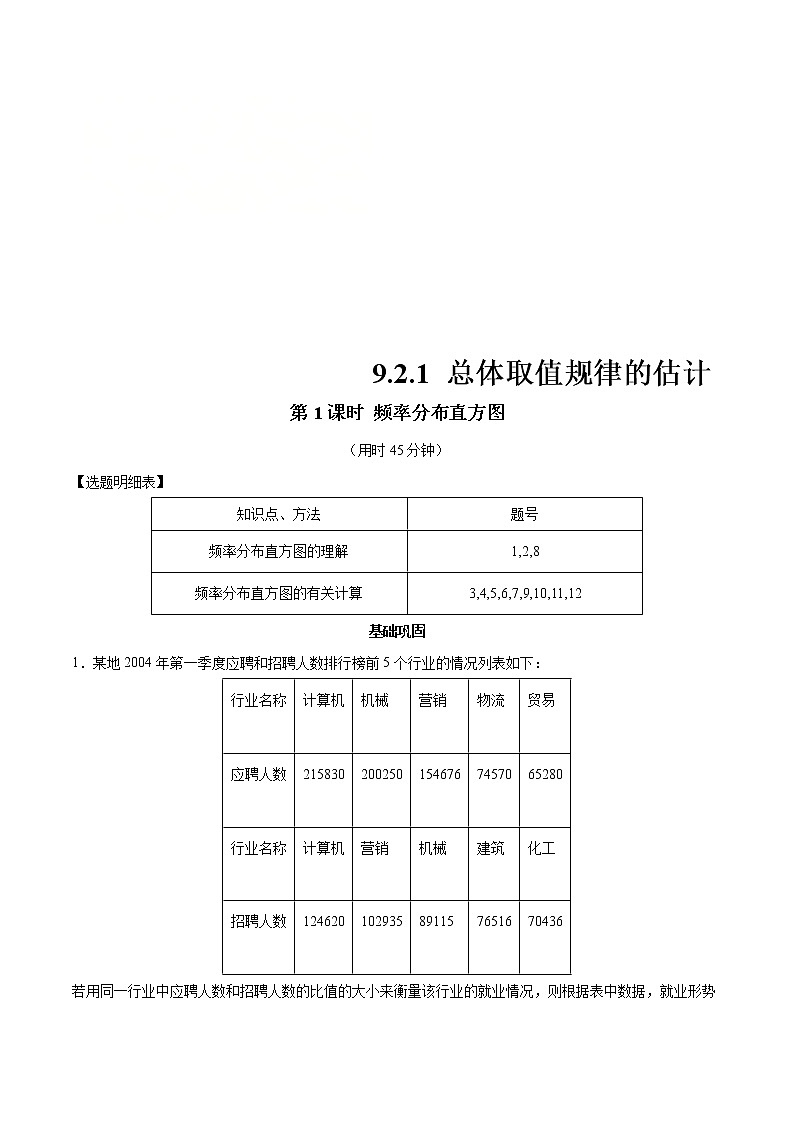
9.2.1 总体取值规律的估计第1课时 频率分布直方图（用时45分钟）【选题明细表】 知识点、方法题号频率分布直方图的理解1,2,8频率分布直方图的有关计算3,4,5,6,7,9,10,11,12基础巩固1．某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下：行业名称
 计算机
 机械
 营销
 物流
 贸易
 应聘人数
 215830
 200250
 154676
 74570
 65280
 行业名称
 计算机
 营销
 机械
 建筑
 化工
 招聘人数
 124620
 102935
 89115
 76516
 70436
 若用同一行业中应聘人数和招聘人数的比值的大小来衡量该行业的就业情况，则根据表中数据，就业形势一定是（    ）A．计算机行业好于化工行业 B．建筑行业好于物流行业C．机械行业最紧张 D．营销行业比贸易行业紧张【答案】B【解析】就业形势的好坏，主要看招聘人数与应聘人数的比值，比值越大，就业形势越好，故选B．2．在一次模拟考试后，从高三某班随机抽取了20位学生的数学成绩，其分布如下：分组频数126731分数在130分（包括130分）以上者为优秀，据此估计该班的优秀率约为（    ）A．10% B．20% C．30% D．40%【答案】B【解析】由表可知：优秀的人数为，则优秀率为：据此估计该班的优秀率约为故选：3．某工厂对一批元件进行抽样检测.经检测，抽出的元件的长度（单位：mm）全部介于93至105之间.将抽出的元件的长度以2为组距分成6组：，，，，，，得到如图所示的频率分布直方图.若长度在内的元件为合格品，根据频率分布直方图，估计这批元件的合格率是（    ）A．80% B．90% C．20% D．85.5%【答案】A【解析】由频率分布直方图可知元件长度在内的频率为：，故这批元件的合格率约为80%.故选：A.4．某校从高一年级学生中随机抽取部分学生，将他们的模块测试成绩分成6组：[40,50), [50,60), [60,70), [70,80), [80,90), [90,100]加以统计，得到如图所示的频率分布直方图．已知高一年级共有学生600名，据此估计，该模块测试成绩不少于60分的学生人数为（ ）A．588 B．480 C．450 D．120【答案】B【解析】据频率分布直方图，得；该模块测试成绩不少于60分的频率是1-（0.005+0.015）×10=0.8，∴对应的学生人数是600×0.8=4805．学校为了调查学生在课外读物方面的支出情况，抽取了一个容量为的样本，其频率分布直方图如图所示，其中支出在的同学有人，则的值为（   ）A． B． C． D．【答案】A【解析】由频率分布直方图可知，支出在的同学的频率为：本题正确选项：6．为了解某校今年准备报考飞行员学生的体重情况，将所得的数据整理后，画出了频率分布直方图(如图)，已知图中从左到右的前3个小组的频率之比为1∶2∶3，其中第2小组的频数为12，则报考飞行员的总人数是________．【答案】48【解析】设图中从左到右的第1小组的频率为，则第2小组的频率为，第3小组的频率为，由频率分布直方图的性质，得：，解得：，第2小组的频率为，又已知第2小组的频数为12，报考飞行员的学生人数是：.故答案应填：48.7．某校100名学生的数学测试成绩的频率分布直方图如图所示，分数不低于a即为优秀，如果优秀的人数为20，则a的估计值是__________.【答案】133【解析】由题意可知：90﹣100分的频率为0.005×10=0.05，频数为5人则100﹣110分的频率为0.018×10=0.18，频数为18人110﹣120分的频率为0.03×10=0.3，频数为30人120﹣130分的频率为0.022×10=0.22，频数为22人130﹣140分的频率为0.015×10=0.15，频数为15人140﹣150分的频率为0.010×10=0.05，频数为10人而优秀的人数为20人，140﹣150分有10人，130﹣140分有15人，取后10人∴分数不低于133即为优秀，8．调查某校高三年级男生的身高，随机抽取40名高三男生，实测身高数据（单位：cm）如下：171163163166166168168160168165171169167169151168170168160174165168174159167156157164169180176157162161158164163163167161（1）作出频率分布表；（2）画出频率分布直方图.【答案】（1）分布表见解析  （2）直方图见解析【解析】（1）最低身高151 cm,最高身高180 cm,它们的差是,即极差为29.确定组距为4,组数为8,频率分布表如下：分组频数频率10.02530.07560.1590.225140.3530.07530.07510.025合计401（2）组距为4,结合频率分布表,可计算各组的,即可得频率分布直方图如下图所示.能力提升9．某校为了对初三学生的体重进行摸底调查，随机抽取了50名学生称其体重（单位：kg），将所得数据整理后画出了频率分布直方图如图所示，体重在内适合跑步训练，体重在内适合跳远训练，体重在内适合投掷训练，估计该校初三学生适合参加跑步、跳远、投掷三项训练的人数之比为（    ）A．4：3：1 B．5：3：1C．5：3：2 D．3：2：1【答案】B【解析】体重在内的频率为，体重在内的频率为，体重在内的频率为，，可估计该校初三学生适合参加跑步、跳远投掷三项训练的人数之比为5：3：1，故选：10．某中学举行了一次“环保知识竞赛”，全校学生参加了这次竞赛.为了了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）作为样本进行统计.若下面是尚未完成并有局部污损的频率分布表和频率分布直方图（如图所示），则的值为______ .分组频数频率80.16■200.40■0.082合计■1 【答案】510【解析】设样本量为，则，所以的频数为，则，，由频率分布直方图的纵轴为频率/组距可得,，，所以.故答案为:11．某家庭记录了未使用节水龙头天的日用水量数据（单位：）和使用了节水龙头天的日用水量数据，得到频数分布表如下：未使用节水龙头天的日用水量频数分布表日用水量频数使用了节水龙头天的日用水量频数分布表日用水量频数（1）在答题卡上作出使用了节水龙头天的日用水量数据的频率分布直方图：（2）估计该家庭使用节水龙头后，日用水量小于的概率；（3）估计该家庭使用节水龙头后，一年能节省多少水？（一年按天计算，同一组中的数据以这组数据所在区间中点的值作代表．）【答案】（1）直方图见解析；（2）；（3）.【解析】（1）频率分布直方图如下图所示：（2）根据以上数据，该家庭使用节水龙头后天日用水量小于的频率为；因此该家庭使用节水龙头后日用水量小于的概率的估计值为；（3）该家庭未使用节水龙头天日用水量的平均数为．该家庭使用了节水龙头后50天日用水量的平均数为．估计使用节水龙头后，一年可节省水．素养达成12．我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准（吨）、一位居民的月用水量不超过的部分按平价收费，超出的部分按议价收费.为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照,分成9组，制成了如图所示的频率分布直方图.（1）求直方图中的值；（2）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；（3）若该市政府希望使的居民每月的用水量不超过标准（吨），估计的值，并说明理由.【答案】（1）；（2）万；（3）.【解析】（1）由频率分布直方图知，月均用水量在[0,0.5)中的频率为0.08×0.5=0.04，同理，在[0.5,1)，[1.5,2)，[2,2.5)，[3,3.5)，[3.5,4)，[4,4.5)中的频率分别为0.08，0.20，0.26，0.06，0.04，0.02．由0.04+0.08+0.5×a+0.20+0.26+0.5×a+0.06+0.04+0.02=1，解得a=0.30．（2）由（1），100位居民每人月均用水量不低于3吨的频率为0.06+0.04+0.02=0.12．由以上样本的频率分布，可以估计全市30万居民中月均用水量不低于3吨的人数为300 000×0.12="36" 000．（3）因为前6组的频率之和为0.04+0.08+0.15+0.20+0.26+0.15=0.88>0.85，而前5组的频率之和为0.04+0.08+0.15+0.20+0.26=0.73<0.85，所以2.5≤x<3．由0.3×(x–2.5)=0.85–0.73，解得x=2.9．所以，估计月用水量标准为2.9吨时，85%的居民每月的用水量不超过标准．