






人教A版 (2019)必修 第一册第四章 指数函数与对数函数本章综合与测试课文ppt课件
展开专题一 指数与对数的运算问题例1计算下列各式的值:
分析:(1)利用指数式与对数式的互化和换底公式;(2)利用指数的运算性质和整体代入.
归纳总结指数与对数的运算是指数、对数应用的前提,也是研究指数函数与对数函数的基础,不仅是本章考查的重点,也是高考的重要考点之一.进行指数式的运算时,要注意运算或化简的先后顺序,一般应将负指数转化为正指数、将根式转化为指数式后再计算或化简,同时注意幂的运算性质的应用;对数运算要注意对数运算性质的正用与逆用,注意对底数的转化、对数恒等式以及换底公式的灵活运用,还要注意对数运算与指数运算之间的关系及其合理地转化.
变式训练1设a=lg0.20.3,b=lg20.3,则( )A.a+b
例4画出函数y=lg4(x2-2x+1)的图象.分析:先要找出这个函数所对应的基本初等函数,然后利用图象变换向目标靠拢.解:先对函数解析式进行化简,可得y=lg2|x-1|.可直接利用描点法画出y=lg2x的图象,而后画出关于y轴的对称变换得到y=lg2|x|,再将整个函数图象向右平移一个单位长度.过程如下:
例5若f(x)=lg(x2-2ax+1+a)在区间(-∞,1]上是减函数,则a的取值范围为( )A.[1,2)B.[1,2]C.[1,+∞)D.[2,+∞)答案:A
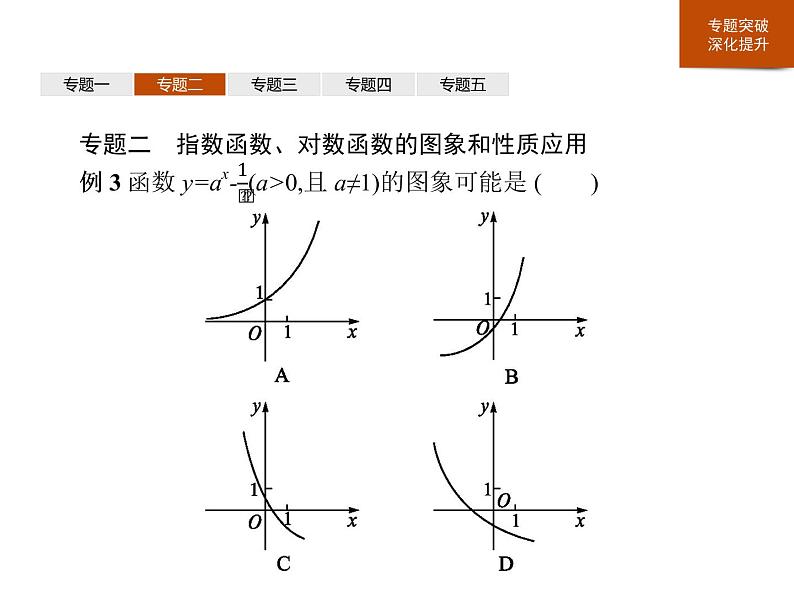
归纳总结指数函数、对数函数及幂函数是重要的基本初等函数.它们的图象与性质始终是高考考查的重点.由于指数函数y=ax(a>0,a≠1,x∈R),对数函数y=lgax(a>0,a≠1,x>0)的图象与性质都与a的取值有密切联系,幂函数y=xα的图象与性质与α的取值有关,因此,在a,α的值不确定时,要对它们进行分类讨论,利用图象可以快捷、直观地解决比较大小、求根等计算烦琐问题.
变式训练3已知a=lg2e,b=ln 2,c= ,则a,b,c的大小关系为( )A.a>b>cB.b>a>cC.c>b>aD.c>a>b解析:因为c= =lg23,a=lg2e,且y=lg2x在(0,+∞)上单调递增,所以lg23>lg2e>lg22=1,即c>a>1.因为y=ln x在(0,+∞)上单调递增,且b=ln 2,所以ln 2
专题三 分类讨论思想在解题中的应用例6比较lgx(2x)与lgx(3-2x)的大小.
归纳总结分类讨论思想即对问题中的参数不能一概而论,需要按一定的标准进行分别阐述,在分类讨论中要做到“不重复,不遗漏”.
变式训练4已知函数f(x)=lga(x+3)在区间[-2,-1]上总有|f(x)|<2,求实数a的取值范围.解:当-2≤x≤-1时,有1≤x+3≤2,由|f(x)|<2,∴-2
专题四 数形结合思想在解题中的应用例7若方程mx-x-m=0(m>0,m≠1)有两个不同的实数解,则m的取值范围是( )A.(1,+∞)B.(0,1)C.(0,+∞)D.(2,+∞)解析:方程mx-x-m=0有两个不同的实数解,即函数y=mx与y=x+m的图象有两个不同的公共点.显然,当m>1时,两图象有两个不同的交点;当0
变式训练5设方程lg x+x=3的实数解为x0,则x0所在的一个区间是( )A.(3,+∞)B.(2,3)C.(1,2)D.(0,1)解析:由lg x+x=3得lg x=3-x.分别画出方程lg x=3-x两边对应的函数图象,如图所示.由图知它们的交点x0在区间(2,3)内.答案:B
人教A版 (2019)选择性必修 第一册第二章 直线和圆的方程2.4 圆的方程教学演示课件ppt: 这是一份人教A版 (2019)选择性必修 第一册第二章 直线和圆的方程2.4 圆的方程教学演示课件ppt,共29页。PPT课件主要包含了内容索引,知识网络整合构建,题型突破深化提升等内容,欢迎下载使用。
高中数学人教版新课标A必修1第三章 函数的应用综合与测试教案配套课件ppt: 这是一份高中数学人教版新课标A必修1第三章 函数的应用综合与测试教案配套课件ppt,共30页。PPT课件主要包含了第三章,函数的应用,章末整合提升,知识结构,要点归纳,专题突破,典例1,典例2,典例3,典例4等内容,欢迎下载使用。
2020-2021学年第一章 集合与函数概念综合与测试备课课件ppt: 这是一份2020-2021学年第一章 集合与函数概念综合与测试备课课件ppt,共50页。PPT课件主要包含了第一章,集合与函数概念,章末整合提升,知识结构,要点归纳,专题突破,典例1,典例2,典例3,典例4等内容,欢迎下载使用。













