浙教版九年级上册第4章 相似三角形4.3 相似三角形集体备课课件ppt

这是一份浙教版九年级上册第4章 相似三角形4.3 相似三角形集体备课课件ppt，文件包含43相似三角形pptx、43相似三角形doc、电子教案43相似三角形doc等3份课件配套教学资源，其中PPT共17页， 欢迎下载使用。
理解相似三角形的概念及相似比，掌握相似三角形判定的预备定理的有关证明.会用平行线判定两个三角形相似并进行证明和计算.（重点、难点）
知识点1 相似三角形
经过相似变换后得到的像与原像称为相似图形.
那么，将一个三角形作相似变换后所得到的像与原像称为相似三角形.
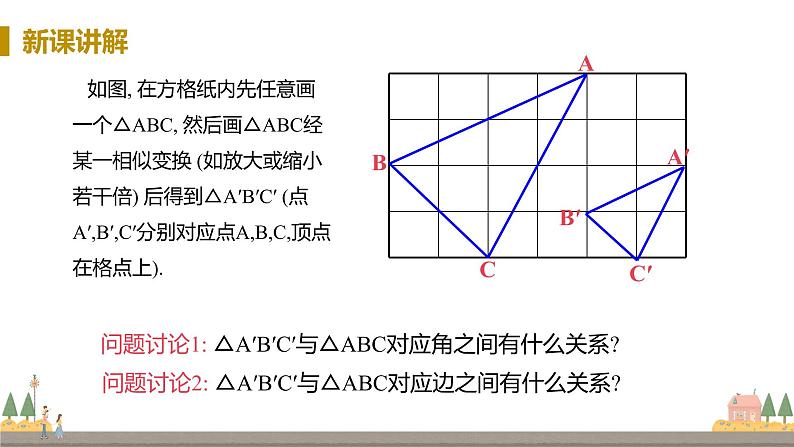
如图, 在方格纸内先任意画一个△ABC, 然后画△ABC经某一相似变换 (如放大或缩小若干倍) 后得到△A′B′C′ (点A′,B′,C′分别对应点A,B,C,顶点在格点上).
问题讨论1: △A′B′C′与△ABC对应角之间有什么关系?
问题讨论2: △A′B′C′与△ABC对应边之间有什么关系?
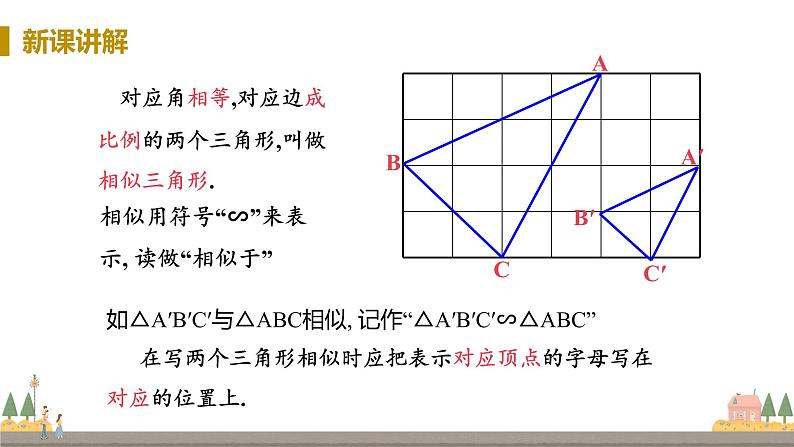
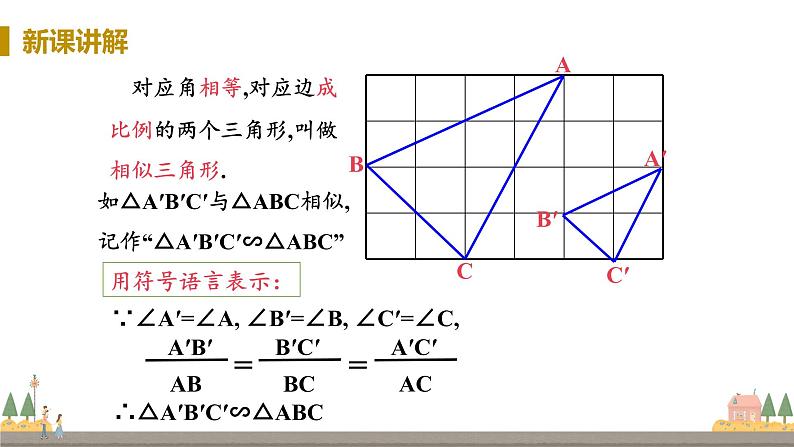
对应角相等,对应边成比例的两个三角形,叫做相似三角形.
相似用符号“∽”来表示, 读做“相似于”
如△A′B′C′与△ABC相似, 记作“△A′B′C′∽△ABC”
在写两个三角形相似时应把表示对应顶点的字母写在对应的位置上.
∴△A′B′C′∽△ABC
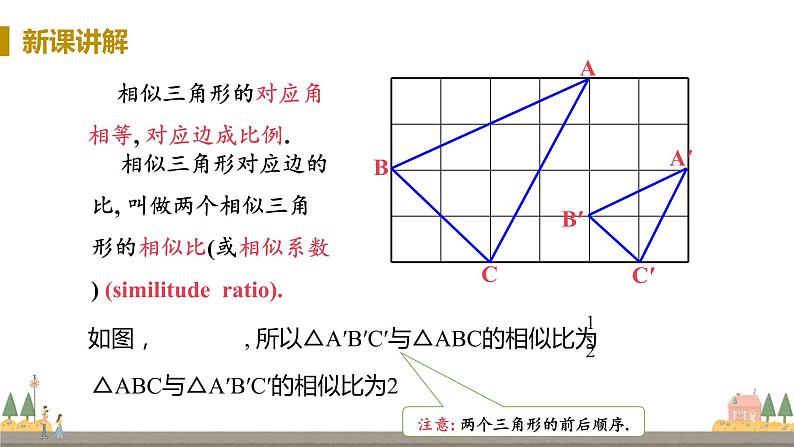
相似三角形的对应角相等, 对应边成比例.
相似三角形对应边的比, 叫做两个相似三角形的相似比(或相似系数) (similitude rati).
△ABC与△A′B′C′的相似比为2
已知:如图, D, E分别是AB, AC边的中点. 求证: △ADE∽△ABC.
∵D，E分别是AB，AC的中点，
∴∠ADE=∠B，∠AED=∠C
在△ADE和△ABC中，
∠ADE=∠B，∠AED=∠C，∠A=∠A
１、两个全等三角形一定相似吗？为什么？
２、两个直角三角形一定相似吗？为什么？ 两个等腰直角三角形呢？
相似. 因为对应角相等, 对应边成比例.
两个直角三角形不一定相似. 因为对应角不一定相等, 对应边也不一定成比例; 两个等腰直角三角形相似 . 因为对应角相等, 对应边成比例.
３、两个等腰三角形一定相似吗？为什么？ 两个等边三角形呢？
两个等腰三角形不一定相似;两个等边三角形相似.
相似三角形的传递性：如果△ABC∽△A1B1C1 ， 而△A1B1C1 ∽△A2B2C2 那么△ABC∽△A2B2C2 .
如果△ABC∽△A1B1C1而△A1B1C1 ∽△A2B2C2那么△ABC与△A2B2C2
在方格纸中,每个小格的顶点称为格点,以格点连线为边的三角形叫做格点三角形,如图所示,在10×10的方格中,已知△OAB.
1.作一个格点三角形与△OAB全等.
2.作一个格点三角形与△OAB相似.
3.作一个格点三角形与△OAB相似且与△OAB 共边AB.
三个角对应相等, 三条边对应成比例的两个三角形, 叫做相似三角形(similar trianglec). △ABC与△DEF相似, 就记作:△ABC∽△DEF. 注意：要把表示对应角顶点的字母写在对应的位置上！ 性质：相似三角形的各对应角相等,各对应边对应成比例. 如果△ ABC∽ △DEF, 那么∠A = ∠D,∠B = ∠E, ∠C = ∠F.
1．下列命题中，是真命题的为 ( )A．锐角三角形都相似 B．直角三角形都相似C．等腰三角形都相似 D．等边三角形都相似2．已知△ABC∽△A′B′C′，且相似比为2，则 ( )A．∠A是∠A′的2倍 B．∠A′是∠A的2倍C．AB是A′B′的2倍 D．A′B′是AB的2倍
3.找出如图所示相似三角形的对应边和对应角．①对应边： ，对应角： ；②对应边： ，对应角： ；③对应边： ，对应角： ．
AD与AB，AE与AC，DE与BC
∠A与∠A，∠ADE与∠B，∠AED与∠C
AO与BO，CO与DO，AC与BD
∠A与∠B，∠C与∠D，∠AOC与∠BOD
DE与DG，DF与DH，EF与GH
∠E与∠G，∠EDF与∠GDH，∠F与∠H