初中数学第十二章 全等三角形12.2 三角形全等的判定导学案

这是一份初中数学第十二章 全等三角形12.2 三角形全等的判定导学案，文件包含122三角形全等的判定讲义学生版docx、122三角形全等的判定讲义教师版docx等2份学案配套教学资源，其中学案共65页， 欢迎下载使用。

1、理解和掌握全等三角形判定方法1——“边边边”
2、理解和掌握全等三角形判定方法2——“边角边”．
3、理解和掌握全等三角形判定方法3——“角边角”，判定方法4——“角角边”；能运用它们判定两个三角形全等．
4、掌握判定直角三角形全等的一种特殊方法一“斜边、直角边” （即“HL”）
教学重难点：判定全等的思路，及全等判定和性质的综合应用
知识点一：“SSS”定理（重点）
判定定理1：SSS--三条边分别对应相等的两个三角形全等．
例题．如图，EF=BC，DF=AC，DA=EB．求证：∠F=∠C．

变式1．已知：如图，点A、D、C、B在同一条直线上，AD=BC，AE=BF，CE=DF，求证：AE∥BF．

变式2．如图，在△ABC中，AB=AC，D，E分别为两腰AB，AC的中点，F，G是BC边上的两点，且BF=CG，连结DG，EF，交点为H，求证：HF=HG．

知识点二：“SAS”定理（重点）
判定定理2：SAS--两边及其夹角分别对应相等的两个三角形全等．
例题．如图，点B，D，C，F在一条直线上，AB=EF，∠ABC=∠EFD，BD=CF．
证明：AC=DE．

变式1．如图，△ABC中，AB=AC，点E，F在边BC上，BE=CF，点D在AF的延长线上，AD=AC．
（1）求证：△ABE≌△ACF；
（2）若∠BAE=30°，则∠ADC= °．

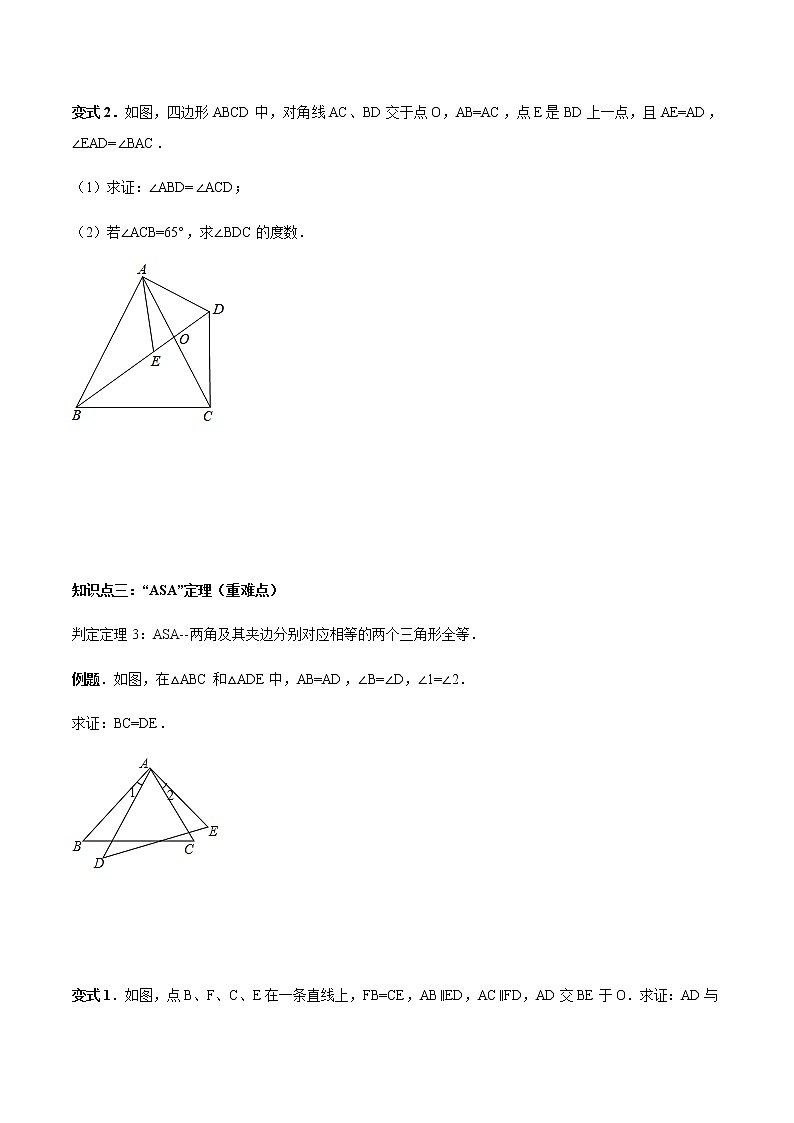
变式2．如图，四边形ABCD中，对角线AC、BD交于点O，AB=AC，点E是BD上一点，且AE=AD，∠EAD=∠BAC．
（1）求证：∠ABD=∠ACD；
（2）若∠ACB=65°，求∠BDC的度数．

知识点三：“ASA”定理（重难点）
判定定理3：ASA--两角及其夹边分别对应相等的两个三角形全等．
例题．如图，在△ABC和△ADE中，AB=AD，∠B=∠D，∠1=∠2．
求证：BC=DE．

变式1．如图，点B、F、C、E在一条直线上，FB=CE，AB∥ED，AC∥FD，AD交BE于O．求证：AD与BE互相平分．
变式2．如图，已知：AD是BC上的中线，BE∥CF．求证：DF=DE．

知识点四：“AAS”定理（重难点）
判定定理4：AAS--两角及其中一个角的对边对应相等的两个三角形全等．
例题．如图，D是△ABC的边AB上一点，DF交AC于点E，DE=FE，FC∥AB，求证：AD=CF．

变式1．如图所示，已知BE⊥AC于点E，CF⊥AB于点F，BE、CF相交于点，BD=CD，连接AD并延长，求证：AD平分∠BAC．

变式2．如图，四边形ABCD中，DC∥AB，BD⊥AD，∠A=45°，E，F分别是AB、CD上的点，且BE=DF，连接EF交BD于O．
（1）求证：BO=DO；
（2）若EF⊥AB，延长EF交AD的延长线于G，当FG=1时，求AE的长．
知识点五：“HL”定理（重难点）
判定定理5：HL--斜边与直角边对应相等的两个直角三角形全等．
例题．如图所示，在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF．
求证：Rt△ABE≌Rt△CBF．

变式1．如图，AD⊥BC于D，AD=BD，AC=BE．
（1）请说明∠1=∠C；
（2）猜想并说明DE和DC有何特殊关系．

变式2．如图，AB=AC，∠BAC=90°，BD⊥AE于D，CE⊥AE于E，且BD＞CE．
求证：BD=EC+ED．

拓展点一：判定三角形全等的思路
方法指引：全等三角形的5种判定方法中，选用哪一种方法，取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两角对应相等，则必须再找一组对边对应相等，且要是两角的夹边，若已知一边一角，则找另一组角，或找这个角的另一组对应邻边．
例题．如图，已知：∠B=∠DEF，BC=EF，现要证明△ABC≌△DEF，
若要以“SAS”为依据，还缺条件 ；
若要以“ASA”为依据，还缺条件 ；
若要以“AAS”为依据，还缺条件 ，并说明理由．
变式1．在△ABC中，∠BAC=90°，AB=AC，D为BC中点，且AE=CF．求证：△AED≌△CFD．
变式2．已知：如图，AC=EC，E、A、D在同一条直线上，∠1=∠2=∠3．试说明：△ABC≌△EDC．

变式3．如图，在△ABC中，∠BAC=90°，AB=AC，点D是AB的中点，连接CD，过B作BE⊥CD交CD的延长线于点E，连接AE，过A作AF⊥AE交CD于点F．
（1）求证：AE=AF；
（2）求证：CD=2BE+DE．
拓展点二：全等三角形性质与判断的综合应用
（1）全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．
（2）在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．
例题．如图，四边形ABCD中，对角线AC、BD交于点O，AB=AC，点E是BD上一点，且AE=AD，∠EAD=∠BAC．
（1）求证：∠ABD=∠ACD；
（2）若∠ACB=65°，求∠BDC的度数．
变式1．如图，∠BAD=∠CAE=90°，AB=AD，AE=AC．
（1）证明：BC=DE；
（2）若AC=12，CE经过点D，求四边形ABCD的面积．

变式2．已知：如图1所示，等腰直角三角形ABC中，∠BAC=90°，AB=AC，直线MN经过点A，BD⊥MN于点D，CE⊥MN于点E．
（1）试判断线段DE、BD、CE之间的数量关系，并说明理由；
（2）当直线MN运动到如图2所示位置时，其余条件不变，判断线段DE、BD、CE之间的数量关系．

拓展点三：全等三角形的计数问题
例题．如图，在△ABC中，∠A=36°，AB=AC，CD、BE分别是∠ACB，∠ABC的平分线，CD、BE相交于F点，连接DE，则图中全等的三角形有多少组（ ）
A．3B．4C．5D．6
变式1．如图，在△ABC中，AB=AC，高BD，CE交于点O，AO交BC于点F，则图中共有全等三角形（ ）
A．7对B．6对C．5对D．4对
变式2．如图，△ABC中，AD⊥BC，AB=AC，AE=AF，则图中全等三角形的对数有（ ）
A．5对B．6对C．7对D．8对
拓展点四：全等三角形中的计算与推理
例题．如图，在△ABC中，∠ABC=2∠C，∠BAC的平分线AD交BC于D，E为AC上一点，AE=AB，连接DE．
（1）求证：△ABD≌△AED；
（2）已知BD=5，AB=9，求AC长．
变式1．如图，已知BE⊥AD，CF⊥AD，且BE=CF．
（1）请你判断AD是△ABC的中线还是角平分线？并证明你的结论．
（2）在（1）的条件下，若AB=6，AC=4，请确定AD的值范围．

变式2．在△ABC中，AB=AC，点D是BC上一点（不与B，C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．
（1）如图1，若∠BAC=90°，
①求证；△ABD≌△ACE；
②求∠BCE的度数．
（2）设∠BAC=α，∠BCE=β．如图2，则α，β之间有怎样的数量关系？请直接写出你的结论．

拓展点五：实际应用问题
例题．如图，A、B两建筑物位于河的两岸，要测得它们之间的距离，可以从B点出发沿河岸画一条射线BF，在BF上截取BC=CD，过D作DE∥AB，使E、C、A在同一直线上，则DE的长就是A、B之间的距离，请你说明道理．

变式1．小明不慎将一块三角形的玻璃打碎成如图所示的四块（图中所标1、2、3、4），你认为将其中的哪一块带去，就能配一块与原来大小一样的三角形玻璃？应该带 去，说明理由．
变式2．如图是小磊家的两个房间甲与乙，他将一个梯子斜靠在墙上，梯子顶端距离地面的垂直距离记作MA，如果梯子的底端不动，顶端靠在对面墙上，此时梯子的顶端距离地面的垂直距离记作NB．
（1）当他在甲房间时，测得MA=a，NB=b，求甲房间的宽AB；
（2）当他在乙房间时，测得MA=c，NB=d，且∠MPA=75°，∠NPB=45°
①求∠MPN的度数；
②求乙房间的宽AB．

拓展点六：图形变换中全等三角形的探究题
例题．（1）如图，△ABC中，∠BAC=90°，AB=AC，AE是过点A的一条直线，且点B，C在AE的同侧，BD⊥AE于D，CE⊥AE于E．求证：BD=DE﹣CE；
（2）上题中，变成如图，B，C在AE的异侧时，BD，DE，CE关系如何？并加以证明．

变式1．如图，已知△ABC中，AB=AC=10cm，BC=8cm，点D为AB的中点．如果点P在线段BC上以3cm/s的速度由点B向C点运动，同时，点Q在线段CA上由点C向A点运动．
（1）若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由．
（2）若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？

变式2．（1）操究发现：如图1，△ABC为等边三角形，点D为AB边上的一点，∠DCE=30°，∠DCF=60°且CF=CD
①求∠EAF的度数；
②DE与EF相等吗？请说明理由
（2）类比探究：如图2，△ABC为等腰直角三角形，∠ACB=90°，点D为AB边上的一点，∠DCE=45°，CF=CD，CF⊥CD，请直接写出下列结果：
①∠EAF的度数
②线段AE，ED，DB之间的数量关系
易错点一：弄错对应关系
例题．如图，点A，D，C，F在一条直线上，AB=DE，∠A=∠EDF，下列条件不能判定△ABC≌△DEF的是（ ）
A．AD=CFB．∠BCA=∠FC．∠B=∠ED．BC=EF
变式1．如图，在△ABC和△DCB中，∠ABC=∠DCB，要使△ABC≌△DCB，还需添加一个条件，这个条件不一定是（ ）
A．∠A=∠DB．∠ACB=∠DBCC．AB=DCD．AC=DB
变式2．如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB=AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD（ ）
A．∠B=∠CB．AD=AEC．BD=CED．BE=CD
易错点二：错用等式性质证全等