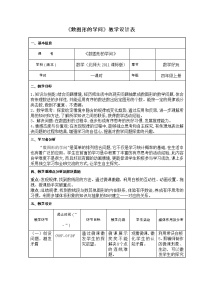
2020-2021学年3 数图形的学问教学设计

《数图形的学问》微课教学设计

教学目标：

1、结合问题情境，经历把生活中的现实问题抽象成数图形的数学问题，并利用多样化的画图策略解决问题的过程，发展几何直观。

2、在数图形的过程中，能够用分类数或者根据图形的规律进行数数，逐步形成有序思考的良好习惯，做到不重复，不遗漏，发展推理能力。

3、在发现规律的进程中，能够独立思考和自主探究，有条理地表达解决问题的过程和结果，增强学习的自信心，提高对数学问题探索的兴趣。

教学过程：

大家好，今天我们一起来学习《数图形的学问》。

鼹鼠家族在矿地上干活，故事开始了，小鼹鼠在工作的时候不注意，将地面凿出了一条裂缝，滚烫的岩浆正从裂缝中涌出，如果不快点逃命的话可能就要被岩浆吞没了，快帮助鼹鼠逃离矿井吧！

同学们，鼹鼠任选一个洞口进入，向前走，再任选一个洞口钻出来，一共有多少条不同的逃生路线呢？

首先，我们画出示意图，用A,B,C,D分别表示4个洞口，想办法按照顺序，数出有多少条不同的路线，要做到不重复不遗漏。

在这里我给大家介绍两种方法：

第一种方法：

先数最短的线段AB,BC,CD,有3条；

再数较长的线段AC,BD,有2条；

最后数最长的线段AD有1条。

最后得到一共有3+2+1=6（条），所以有6条不同的路线。

第二种方法：

先数从A点出发的线段AB,AC,AD,有3条；

再数从B点出发的线段BC,BD,有2条；

最后数从C点出发的线段CD有1条。

最后也可以得到一共有3+2+1=6（条）。也就是说，不管你用哪种方法，4个洞口，画出的示意图中有3条基本线段，最后结果是3+2+1=6（条）。

同学们，你们再认真思考一下，如果鼹鼠钻出5个洞口，6个洞口，7个洞口，8个洞口，又分别会有多少种不同的逃生路线呢？

同理，利用上面数形结合的方法，任选其中的一种数数方法都可以发现以下的规律：

5个洞口，就会有4条基本线段，路线总数为：4+3+2+1；

6个洞口，就会有5条基本线段，路线总数为：5+4+3+2+1；

7个洞口，就会有6条基本线段，路线总数为：6+5+4+3+2+1；

8个洞口，就会有7条基本线段，路线总数为：7+6+5+4+3+2+1；

那么，同学们，你们有发现这里面存在的有趣的规律了吗？

鼹鼠钻出n个洞口,就会有n-1条基本线段，路线种数为:（n-1）+（n-2）+ ··· +1综上，我们就可以把几何的数线段问题转化为代数的问题，列式解答了，这种方法在数学上叫数形结合，也是我们今天研究出来的重要技巧和方法。

好，今天的课就到这里，谢谢！

课后反思：

本节微课是《数图形的学问》这一课时内容的一个重要教学环节，首先，微课选用鼹鼠钻洞这一有趣故事（当然故事是本人构思，有待完善）导入课题，充分激发学生的学习兴趣和求知欲。

其次，在解决问题时，把现实中的问题（求不同的逃生路线）演变为数学上的问题（数有多少条不同的线段）。

紧接着在数线段时，强调要做到不重复不遗漏，引导学生用两种不同的数线段方法,很好的做到不重复不遗漏的数出线段种数。并告诉学生这种解决问题的方法用到了我们数学上的常用解决方法：数形结合。

最后，适时提出疑问（如果鼹鼠钻出5个洞口，6个洞口，7个洞口，8个洞口，又分别会有多少条路线呢？），通过多种情况的问题解决，让学生发现规律，并归纳总结为代数上的问题（列算式解答）。

当然了，由于时间的限制，在微课里就只是一个简单的知识解决提升的过程，其实真正的课堂需要留给学生动手操作以及思考讨论的时间，我觉得几何到代数的过程尽可能让学生发现，最后总结出来的规律还可以延伸到解决更多的实际问题，都可以举例说明（由于时间问题，这些微课里并没有涉及到），也让学生有一个更好更深入的了解。