初中数学冀教版八年级上册12.3 分式的加减教学课件ppt

这是一份初中数学冀教版八年级上册12.3 分式的加减教学课件ppt，共19页。PPT课件主要包含了知识回顾，一个条件可以吗，两个条件可以吗，探究活动，三个条件呢，动手试一试，证明的书写步骤，温故知新，课堂小结等内容，欢迎下载使用。

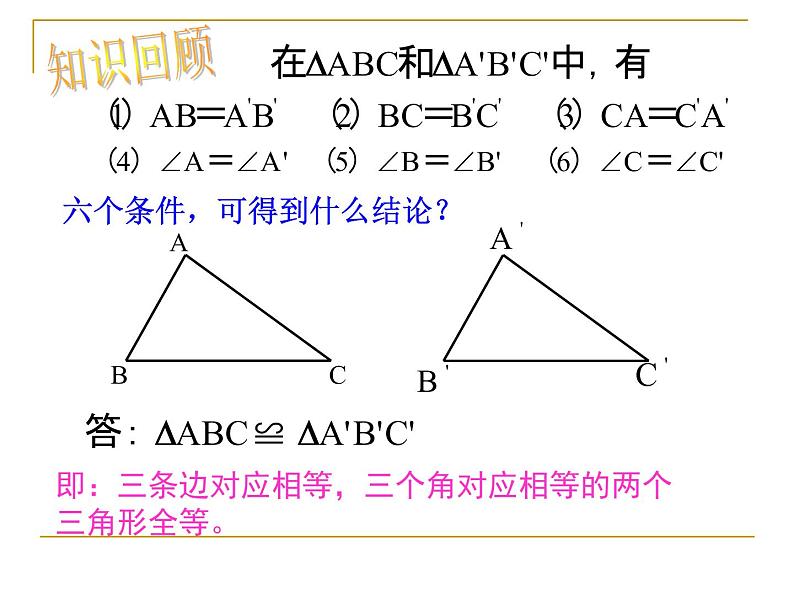
1. 什么叫全等三角形？
能够重合的两个三角形叫 全等三角形。
2.全等三角形有什么性质？全等三角形的对应边相等，对应角相等
即：三条边对应相等，三个角对应相等的两个三角形全等。
六个条件，可得到什么结论？
有一条边相等的两个三角形
2. 有一个角相等的两个三角形
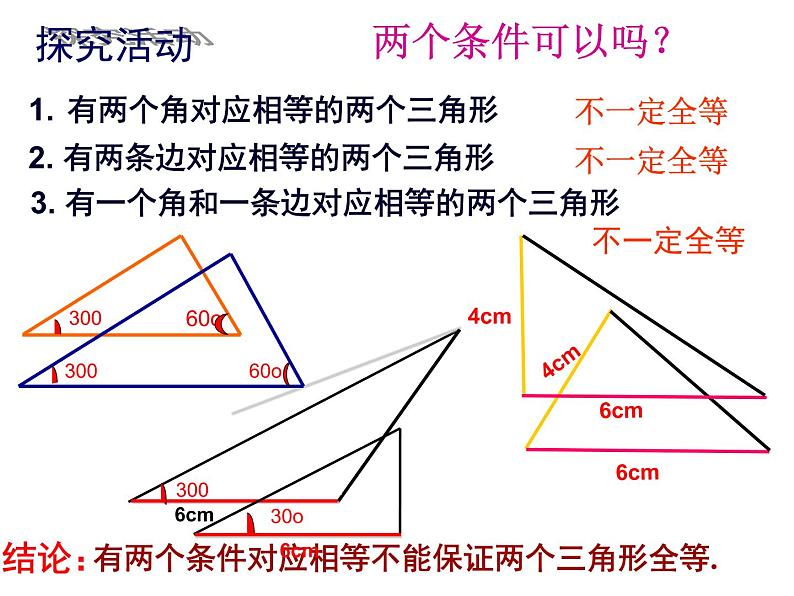
有一个条件相等不能保证两个三角形全等.
有两个条件对应相等不能保证两个三角形全等.
有两个角对应相等的两个三角形
3. 有一个角和一条边对应相等的两个三角形
2. 有两条边对应相等的两个三角形
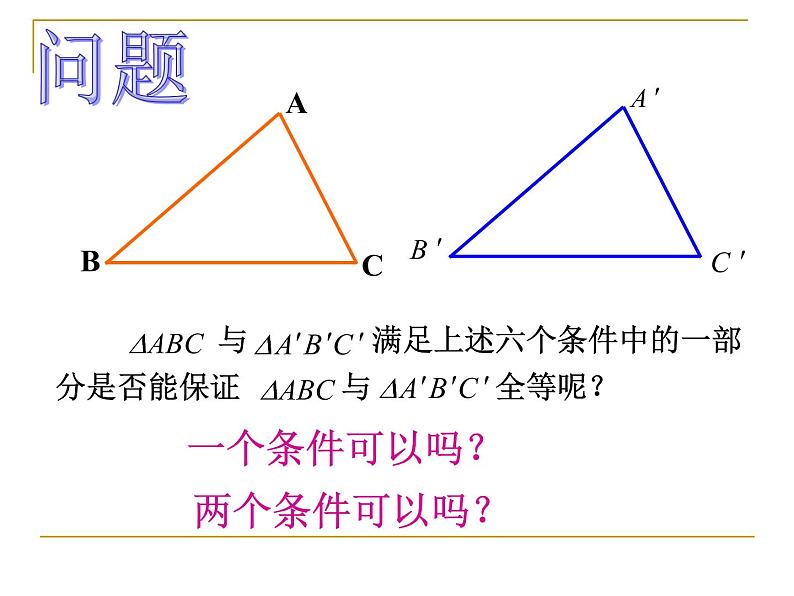
如果给出三个条件画三角形，你能说出有哪几种可能的情况？
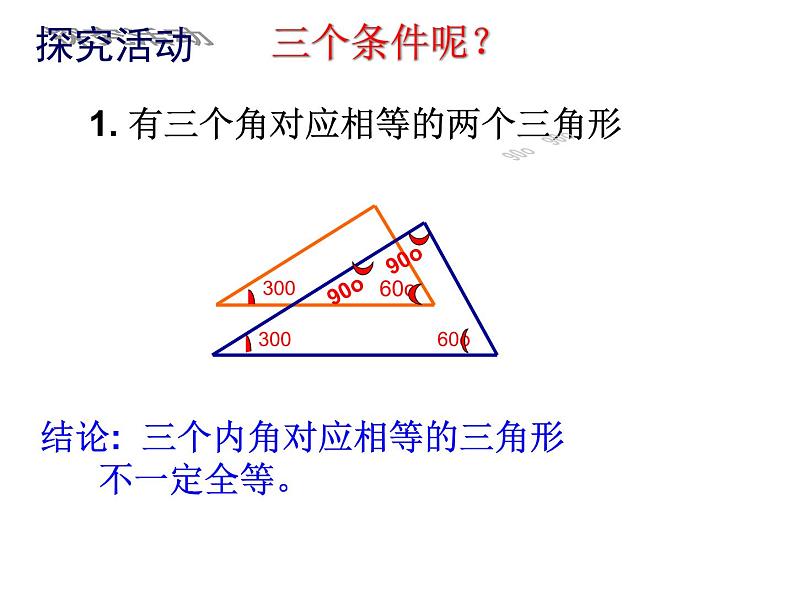
结论: 三个内角对应相等的三角形 不一定全等。
有三个角对应相等的两个三角形
三边相等的两个三角形会全等吗？
三边对应相等的两个三角形全等，简写为“边边边”或“SSS”。
用上面的结论可以判定两个三角形全等．
三边对应相等的两个三角形全等.(简写成“边边边”或“SSS”)
如何用符号语言来表达呢?
∴ ∠A = ∠___ ∠B = ∠___ ∠C = ∠___
∴ △ABC △ADC（SSS）
例1 已知：如图，AB=AD，BC=CD， 求证：△ABC≌ △ADC
AC ( ）
AB=AD ( )BC=CD ( )
证明：在△ABC和△ADC中
判断两个三角形全等的推理过程，叫做证明三角形全等。
①准备条件：证全等时要用的间接条件要先证好；
②三角形全等书写三步骤：
摆出三个条件用大括号括起来
我们曾经做过这样的实验：将三根木条钉成一个三角形木架，这个三角形木架的形状和大小就不变了，你现在能解释其中的道理吗？
三角形的三边长度固定，这个三角形的形状大小就完全确定，这个性质叫三角形的稳定性。
请同学们谈谈本节课的收获与体会
本节课你学到了什么？ 发现了什么？ 还存在什么没有解决的问题？
1.边边边公理：有三边对应相等的两个三角形全等 简写成“边边边”（SSS）
2.边边边公理的应用中所用到的数学方法: 证明线段（或角相等） 证明线段（或角）所在的两个三角形全等.
1. 说明两个三角形全等所需的条件应按对应边的顺序书写.2. 结论中所出现的边必须在所证明的两个三角形中.
用结论说明两个三角形全等需注意