2021-2022学年 初中数学 八年级上册 苏科版 期中检测卷【试卷+答案】

这是一份2021-2022学年 初中数学 八年级上册 苏科版 期中检测卷【试卷+答案】，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
期中检测卷

时间：120分钟　　 满分：130分

一、选择题(每小题3分，共30分)
1.下列图形中，不是轴对称图形的是(　　)
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

2.如图，已知∠ABC=∠DCB，添加以下条件，不能判定△ABC≌△DCB的是(　　)

A.∠A=∠D B.AC=DB
C.∠ACB=∠DBC D.AB=DC
3.已知直角三角形的两条边长分别是8和10，则第三条边长的平方是(　　)
A.36 B.164 C.136 D.36或164
4.在联欢会上，有A，B，C三名选手站在一个三角形的三个顶点的位置上，他们在玩抢凳子游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，凳子应放在最适当的位置(凳子到三名选手的距离相等)，则凳子应放在△ABC的(　　)
A.三边中线的交点 B.三条角平分线的交点 C.三边垂直平分线的交点 D.三边高线的交点
5.给出下列说法：①7，24，25是勾股数；②若等腰三角形的周长为20，一边长为6，则另外两边长是6，8；③若两个三角形全等，则这两个三角形必关于某条直线对称；④三边长分别为6，8，10的三角形的最长边上的中线长为5.其中正确的是(　　)
A.①④ B.①③ C.①② D.③④
6.如图，在四边形ABCD中，AB=AD，CB=CD，若连接AC，BD相交于点O，则图中全等三角形共有(　　)

A.1对 B.2对 C.3对 D.4对
7.一海轮以24海里/时的速度从港口A出发向东南方向航行，另一海轮以18海里/时的速度同时从港口A出发向西南方向航行，离开港口2小时后，两海轮之间的距离为(　　)
A.36海里 B.48海里 C.60海里 D.84海里
8.已知△ABC的三边长分别为4，4，6，在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画(　　)
A.3条 B.4条 C.5条 D.6条
9.如图，四边形ABCD中，∠C=50°，∠B=∠D=90°，E，F分别是BC，DC上的点，当△AEF的周长最小时，∠EAF的度数为(　　)
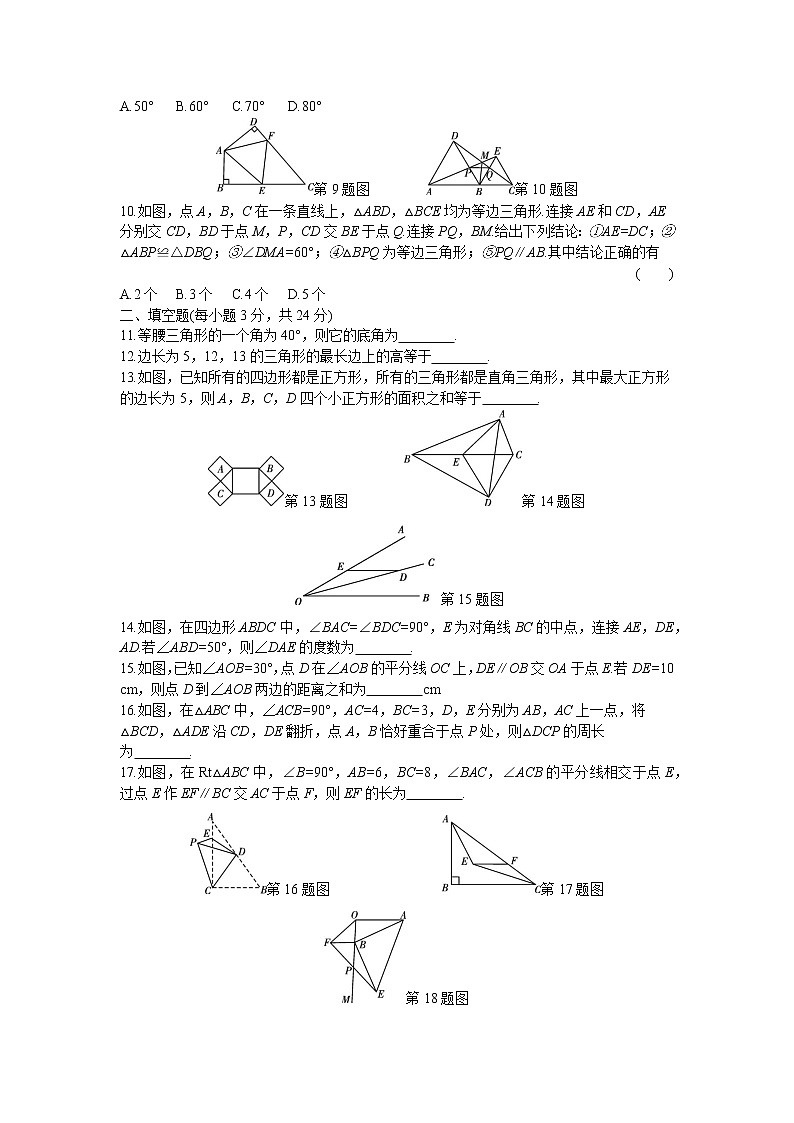
A.50° B.60° C.70° D.80°
第9题图　　　　第10题图
10.如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形.连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q.连接PQ，BM.给出下列结论：①AE=DC；②△ABP≌△DBQ；③∠DMA=60°；④△BPQ为等边三角形；⑤PQ∥AB.其中结论正确的有(　　)
A.2个 B.3个 C.4个 D.5个
二、填空题(每小题3分，共24分)
11.等腰三角形的一个角为40°，则它的底角为　　　　. 
12.边长为5，12，13的三角形的最长边上的高等于　　　　. 
13.如图，已知所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大正方形的边长为5，则A，B，C，D四个小正方形的面积之和等于　　　　. 
第13题图　　　　第14题图　　　　第15题图
14.如图，在四边形ABDC中，∠BAC=∠BDC=90°，E为对角线BC的中点，连接AE，DE，AD.若∠ABD=50°，则∠DAE的度数为　　　　. 
15.如图，已知∠AOB=30°，点D在∠AOB的平分线OC上，DE∥OB交OA于点E.若DE=10 cm，则点D到∠AOB两边的距离之和为　　　　cm. 
16.如图，在△ABC中，∠ACB=90°，AC=4，BC=3，D，E分别为AB，AC上一点，将△BCD，△ADE沿CD，DE翻折，点A，B恰好重合于点P处，则△DCP的周长为　　　　. 
17.如图，在Rt△ABC中，∠B=90°，AB=6，BC=8，∠BAC，∠ACB的平分线相交于点E，过点E作EF∥BC交AC于点F，则EF的长为　　　　. 
第16题图　　　　　　　　第17题图　　　　　　　　第18题图
18.如图，AO⊥OM，OA=8，点B为射线OM上的一个动点，分别以OB，AB为直角边，B为直角顶点，在OM两侧作等腰直角三角形OBF、等腰直角三角形ABE，连接EF交OM于点P，当点B在射线OM上移动时，PB的长度是　　　. 
三、解答题(共76分)
19.(6分)如图，△ABC中，∠BAC=90°，AD⊥BC，垂足为D.求作∠B的平分线，分别交AD，AC于P，Q两点，并证明AP=AQ.(要求：尺规作图，保留作图痕迹，不写作法)






20.(8分)周长为60 cm的△ABC的最长边AB比最短边的2倍还多6 cm，比另一边多2 cm.求该三角形的面积.





21.(8分)如图，在△ABC中，AB=AC，D为AC的中点，DE⊥AB，DF⊥BC，垂足分别为点E，F，且DE=DF.求证：△ABC是等边三角形.


22.(8分)如图，AD∥BC，∠BAC=70°，DE⊥AC于点E，∠D=20°.
(1)求∠B的度数，并判断△ABC的形状；
(2)若延长DE恰好过点B，试说明BD是∠ABC的平分线.









23.(8分)如图，在长度为1个单位长度的小正方形组成的网格中，点A，B，C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB'C'；
(2)△ABC的面积为　　　　； 
(3)以AC为边作与△ABC全等的三角形，则可作出　　　　个三角形与△ABC全等； 
(4)在直线l上找一点P，使PB+PC的长最短.









24.(8分)在小学，我们已经初步了解到，正方形的每个角都是90°，每条边都相等.如图，在正方形ABCD外侧作直线AQ，且∠QAD=30°，点D关于直线AQ的对称点为点E，连接DE，BE，DE交AQ于点G，BE交AQ于点F.
(1)求∠ABE，∠BED的度数；
(2)若AB=6，求FG的长.








25.(8分)如图，在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED=EC.试确定线段AE与DB的大小关系，并说明理由.




26.(10分)如图，在Rt△ABC中，∠C=90°，BD是Rt△ABC的一条角平分线，点O，E，F分别在BD，BC，AC上，且四边形OECF是正方形.
(1)求证：点O在∠BAC的平分线上；
(2)若AC=5，BC=12，求OE的长.



27.(12分)如图1，点P，Q分别是边长为4 cm的等边三角形ABC的边AB，BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1 cm/s.
(1)连接AQ，CP交于点M，则在P，Q运动的过程中，∠CMQ的大小会发生变化吗?若变化，请说明理由，若不变，请求出它的度数.
(2)设点P，Q的运动时间为t s，则当t为何值时，△PBQ是直角三角形?
(3)如图2，若点P，Q在运动到终点后继续在射线AB，BC上运动，直线AQ，CP交于点M，则∠CMQ的大小会发生变化吗?若变化，请说明理由；若不变，请求出它的度数.






期中检测卷
题号
1
2
3
4
5
6
7
8
9
10
答案
A
B
D
C
A
C
C
B
D
D
11.40°或70°　12.6013　13.50　14.40°　15.10　16.8
17.103　18.4

1.A　
2.B　【解析】　已知∠ABC=∠DCB，加上题中隐含的条件BC=CB，可以添加一对角或是添加夹角的另一组边，都可以证明两个三角形全等，故添加A，C，D均可使△ABC≌△DCB.故选B.
3.D　【解析】　若第三条边是直角边，则第三条边长的平方为102-82=36；若第三条边是斜边，则第三条边长的平方为102+82=164.综上，第三条边长的平方是36或164.故选D.
4.C　【解析】　∵三角形三边垂直平分线的交点到三角形三个顶点的距离相等，∴凳子应放在△ABC的三边垂直平分线的交点处.故选C.
5.A　【解析】　∵72+242=252，∴7，24，25是勾股数，∴①正确；若等腰三角形的周长为20，一边长为6，则另外两边长是6，8或7，7，∴②不正确；易知③不正确；根据勾股定理的逆定理，可知三边长为6，8，10的三角形是直角三角形，再根据直角三角形斜边上的中线等于斜边的一半可知该三角形的最长边上的中线长为5，故④正确.综上，正确的是①④.故选A.
6.C　【解析】　∵AB=AD，CB=CD，AC=AC，∴△ABC≌△ADC(SSS).∴∠BAC=∠DAC，∠BCA=∠DCA.又∵AO=AO，CO=CO，∴△ABO≌△ADO(SAS)，△BCO≌△DCO(SAS).综上，图中共有3对全等三角形.故选C.
7.C　【解析】　如图，连接BC.∵两船行驶的方向分别是东南方向和西南方向，∴∠BAC=90°，2小时后，有AC=24×2=48(海里)，AB=18×2=36(海里)，根据勾股定理得，BC2=AB2+AC2=3 600，∴BC=60海里.故选C.


8.B　【解析】　已知AB=AC=4，BC=6.如图，当AC=CD，AB=BG，AF=CF，AE=BE时，都能得到符合题意的等腰三角形(AD，AE，AF，AG分别为分割线).故选B.


9.D　【解析】　如图，分别作点A关于BC和CD的对称点A'，A″，连接A'A″，交BC于点E，交CD于点F，则FA=FA″，EA=EA'，此时△AEF的周长最小，即A'A″的长.∵∠C=50°，∴∠DAB=130°，∴∠AA'E+∠A″=50°.∵EA=EA'，FA=FA″，∴∠EA'A=∠EAA'，∠FAD=∠A″，∴∠EAA'+∠A″AF=50°，∴∠EAF=130°-50°=80°.故选D.

10.D　【解析】　∵△ABD，△BCE均为等边三角形，∴AB=DB，∠ABD=∠CBE=60°，BE=BC，∴∠ABE=∠DBC，∠PBQ=60°.在△ABE和△DBC中，AB=DB，∠ABE=∠DBC，BE=BC，∴△ABE≌△DBC(SAS)，∴AE=DC，∴①正确；∵△ABE≌△DBC，∴∠BAP=∠BDQ.在△ABP和△DBQ中，∠BAP=∠BDQ，AB=DB，∠ABP=∠DBQ，
∴△ABP≌△DBQ(ASA)，∴②正确； ∵∠BAE=∠BDC，∠BDC+∠BCD=∠DBA=60°，∴∠DMA=∠BAE+∠BCD=∠BDC+∠BCD=60°，∴③正确；∵△ABP≌△DBQ，∴BP=BQ，又∵∠PBQ=60°，∴△BPQ为等边三角形，∴④正确；∵△BPQ为等边三角形，∴∠BPQ=60°=∠PBA，∴PQ∥AB，∴⑤正确.综上，正确的结论有5个.故选D.
11.40°或70°　【解析】　分两种情况讨论：若40°是顶角，则底角为70°；若40°是底角，则底角为40°.综上，等腰三角形的底角为40°或70°.
12.6013　【解析】　∵52+122=132，∴该三角形为直角三角形.根据三角形的面积求法，可知最长边上的高为5×1213，即6013.
13.50　【解析】　∵所有的三角形都是直角三角形，∴正方形A和C的面积和等于大正方形的面积，同理，正方形B和D的面积和等于大正方形的面积，∴A，B，C，D四个小正方形的面积为2×5×5=50.
14.40°　【解析】　∵∠BAC=∠BDC=90°，E为对角线BC的中点，∴AE=BE=DE，∴∠BAE=∠ABE，∠DBE=∠BDE，∴∠AED=∠BAE+∠ABE+∠DBE+∠BDE=2∠ABD=100°.∵AE=DE，∴∠DAE=12(180°-∠AED)=12×(180°-100°)=40°.
15.10　【解析】　如图，过点D作DM⊥OB，DN⊥OA，M，N为垂足.∵DE∥OB，∴∠AED=∠AOB=30°，∴DN=12DE=5 cm.∵OD平分∠AOB，DM⊥OB，DN⊥OA，∴DM=DN=5 cm，∴DM+DN=10 cm.

16.8　【解析】　∵将△BCD，△ADE沿CD，DE翻折，点A，B恰好重合于点P处，∴DA=DB=DP.在Rt△ACB中，AB2=BC2+AC2=25，∴AB=5，∴CD=PD=AD=12AB=52，∵CP=CB=3，∴△PCD的周长为PC+DC+DP=8.
17.103　【解析】　如图，过点E分别作ED⊥AB，EM⊥BC，EN⊥AC，垂足分别为D，M，N.∵∠BAC，∠ACB的平分线相交于点E，∴ED=EM=EN.在Rt△ABC中，由勾股定理得AC=10.设ED=EM=EN=x，易知AN=AD=6-x，CN=CM=8-x.∴6-x+8-x=10，∴x=2.∵EF∥BC，∴∠FEC=∠ECB，∵CE平分∠ACB，∴∠FCE=∠ECB，∴∠FEC=∠FCE，∴EF=CF.在Rt△EFN中，NF=CN-CF=8-2-CF=6-EF，∴EF2-(6-EF)2=22，解得EF=103.

18.4　【解析】　如图，过点E作EN⊥BM，垂足为点N，∵∠AOB=∠ABE=∠BNE=90°，∴∠ABO+∠BAO=∠ABO+∠NBE=90°，∴∠BAO=∠NBE.∵△ABE，△BFO均为等腰直角三角形，∴AB=BE，BF=BO.在△ABO和△BEN中，∠BAO=∠EBN，∠AOB=∠BNE，AB=BE，
∴△ABO≌△BEN(AAS)，∴BO=NE，BN=AO.∵BO=BF，∴BF=NE，在△BPF和△NPE中，∠FBP=∠ENP，∠FPB=∠EPN，BF=NE，∴△BPF≌△NPE(AAS)，∴BP=NP=12BN.又∵BN=AO，∴BP=12AO=12×8=4.


19.【解析】　如图，BQ就是所求作的∠ABC的平分线.
证明：

∵AD⊥BC，
∴∠ADB=90°，
∴∠BPD+∠PBD=90°.
∵∠BAC=90°，
∴∠AQP+∠ABQ=90°.
∵∠ABQ=∠PBD，∴∠BPD=∠AQP.
又∵∠BPD=∠APQ，∴∠APQ=∠AQP，∴AP=AQ.
20.【解析】　设该三角形的三边长分别为a cm，b cm，c cm(a