2022届新高考一轮复习苏教版 第8章 第4讲 直线、平面垂直的判定与性质 课件（47张）

这是一份2022届新高考一轮复习苏教版 第8章 第4讲 直线、平面垂直的判定与性质 课件（47张），共47页。PPT课件主要包含了栏目导航，基础整合自测纠偏，素养微专直击高考，重难突破能力提升，配套训练，两条相交直线，a⊥αb⊥α，直二面角，l⊂βl⊥α，典例精析等内容，欢迎下载使用。
1．直线与平面垂直(1)直线和平面垂直的定义：如果一条直线l与平面α内的______直线都垂直，就说直线l与平面α互相垂直．
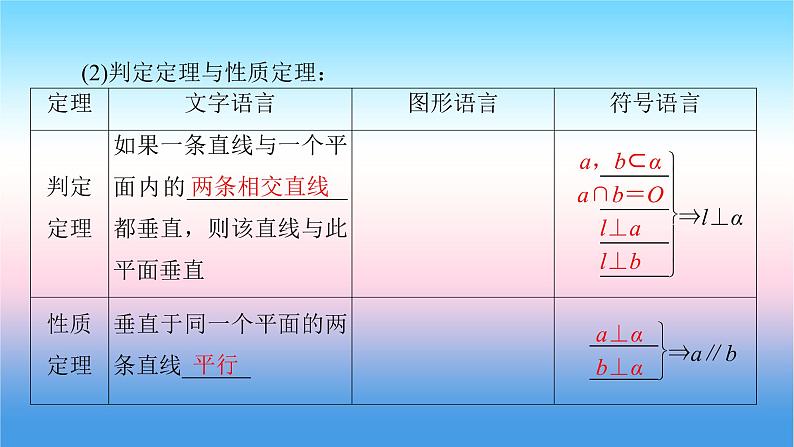
(2)判定定理与性质定理：
a，b⊂α　a∩b＝O　l⊥a　l⊥b　
2．平面与平面垂直(1)平面与平面垂直的定义：两个平面相交，如果它们所成的二面角是__________，就说这两个平面互相垂直．
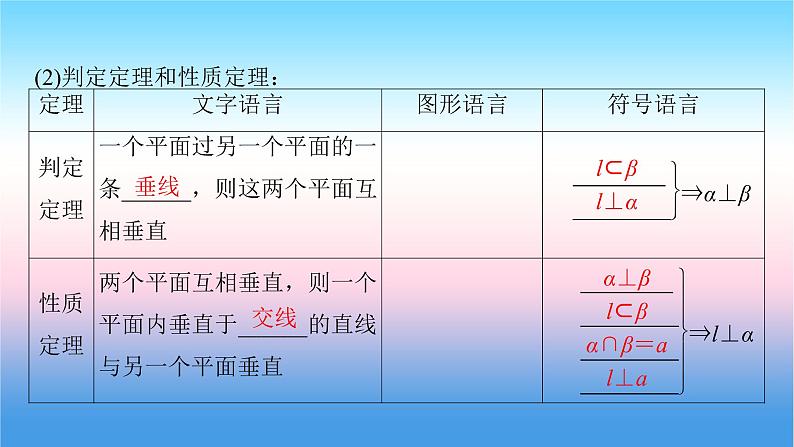
(2)判定定理和性质定理：
α⊥β　l⊂β　α∩β＝a　l⊥a　
【特别提醒】1．在解决直线与平面垂直的问题过程中，要注意直线与平面垂直的定义、判定定理和性质定理的联合交替使用，即注意线线垂直和线面垂直的互相转化．2．面面垂直的性质定理是作辅助线的一个重要依据．要作一个平面的一条垂线，通常是先找这个平面的一个垂面，在这个垂面中，作交线的垂线即可．
【常用结论】直线与平面垂直的五个结论(1)若一条直线垂直于一个平面，则这条直线垂直于这个平面内的任意直线．(2)若两条平行线中的一条垂直于一个平面，则另一条也垂直于这个平面．
(3)垂直于同一条直线的两个平面平行．(4)一条直线垂直于两平行平面中的一个，则这条直线与另一个平面也垂直．(5)两个相交平面同时垂直于第三个平面，它们的交线也垂直于第三个平面．
1．下列命题中错误的是(　　)A．如果平面α⊥平面β，那么平面α内一定存在直线平行于平面βB．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面βC．如果平面α⊥平面γ，平面β⊥平面γ，α∩β＝l，那么l⊥平面γD．如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β【答案】D
2．(2019年安徽江南十校联考)已知m和n是两条不同的直线，α和β是两个不重合的平面，下面给出的条件中一定能推出m⊥β的是(　　)A．α⊥β且m⊂αB．m⊥n且n∥βC．m∥n且n⊥βD．m⊥n且α∥β【答案】C
3．(多选)PA垂直于以AB为直径的圆所在的平面，C为圆上异于A，B两点的任一点，则下列关系正确的是(　　)A．PA⊥BCB．BC⊥平面PACC．AC⊥PBD．PC⊥BC【答案】ABD
4．(教材改编)设α，β为两个不同的平面，直线l⊂α，则“l⊥β”是“α⊥β”成立的(　　)A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】A　【解析】 依题意，由l⊥β，l⊂α，可以推出α⊥β；反过来，由α⊥β，l⊂α不能推出l⊥β，因此“l⊥β”是“α⊥β”成立的充分不必要条件．
5．在三棱锥P－ABC中，点P在平面ABC中的射影为点O.(1)若PA＝PB＝PC，则点O是△ABC的______心．(2)若PA⊥PB，PB⊥PC，PC⊥PA，则点O是△ABC的______心．【答案】(1)外　(2)垂
6．如图，已知∠BAC＝90°，PC⊥平面ABC，则在△ABC，△PAC的边所在的直线中，与PC垂直的直线有____________；与AP垂直的直线有________．【答案】AB，BC，AC　AB　【解析】因为PC⊥平面ABC，所以PC垂直于直线AB，BC，AC．因为AB⊥AC，AB⊥PC，AC∩PC＝C，所以AB⊥平面PAC．又因为AP⊂平面PAC，所以AB⊥AP，与AP垂直的直线是AB．
1．两个平面垂直的性质定理两个平面垂直的性质定理，即如果两个平面垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面是作点到平面距离的依据，要过平面外一点P作平面α的垂线，通常是先作(找)一个过点P并且和α垂直的平面β，设β∩α＝l，在β内作直线a⊥l，则a⊥α.2．两平面垂直的判定(1)两个平面所成的二面角是直角；(2)一个平面经过另一平面的垂线．
判断下面结论是否正确(请在括号中打“√”或“×”)：(1)直线l与平面α内的无数条直线都垂直，则l⊥α.(　　)(2)垂直于同一个平面的两平面平行．(　　)(3)若两平面垂直，则其中一个平面内的任意一条直线垂直于另一个平面．(　　)(4)若平面α内的一条直线垂直于平面β内的无数条直线，则α⊥β.(　　)【答案】(1)×　(2)×　(3)×　(4)×
(2018年新课标Ⅱ)如图，在三棱锥P－ABC中，AB＝BC＝2，PA＝PB＝PC＝AC＝4，O为AC的中点．(1)求证：PO⊥平面ABC；(2)若点M在棱BC上，且MC＝2MB，求点C到平面POM的距离．
直线与平面垂直的判定与性质
【解题技巧】1．证明直线和平面垂直的常用方法(1)判定定理；(2)垂直于平面的传递性(a∥b，a⊥α⇒b⊥α)；(3)面面平行的性质(a⊥α，α∥β⇒a⊥β)；(4)面面垂直的性质．2．证明线面垂直的核心是证明线线垂直，而证明线线垂直则需借助线面垂直的性质．因此，判定定理与性质定理的合理转化是证明线面垂直的基本思想．
平面与平面垂直的判定与性质
【解题技巧】证明面面垂直的2种方法(1)定义法：利用面面垂直的定义，即判定两平面所成的二面角为直二面角，将证明面面垂直问题转化为证明平面角为直角的问题．(2)定理法：利用面面垂直的判定定理，即证明其中一个平面经过另一个平面的一条垂线，把问题转化成证明线线垂直加以解决．
如图，M，N，K分别是正方体ABCD－A1B1C1D1的棱AB，CD，C1D1的中点．求证：(1)AN∥平面A1MK；(2)平面A1B1C⊥平面A1MK.
思想方法类——立体几何证明问题中的转化思想
【考查角度】线面平行的判定定理、线面垂直与面面垂直的判定定理及性质定理．【考查目的】考查数形结合方法、推理能力与计算能力，体现直观想象和逻辑推理的核心素养．【思路导引】(1)要证线面平行，需证线线平行．(2)要证面面垂直，需证线面垂直，要证线面垂直，需证线线垂直．
解：(1)如图，连接NK.在正方体ABCD－A1B1C1D1中，因为四边形AA1D1D，DD1C1C都为正方形，所以AA1∥DD1，AA1＝DD1，C1D1∥CD，C1D1＝CD．因为N，K分别为CD，C1D1的中点，
所以DN∥D1K，DN＝D1K.所以四边形DD1KN为平行四边形．所以KN∥DD1，KN＝DD1．所以AA1∥KN，AA1＝KN.所以四边形AA1KN为平行四边形．所以AN∥A1K.因为A1K⊂平面A1MK，AN⊄平面A1MK，所以AN∥平面A1MK.
(2)如图，连接BC1．在正方体ABCD－A1B1C1D1中，AB∥C1D1，AB＝C1D1．因为M，K分别为AB，C1D1的中点，所以BM∥C1K，BM＝C1K.所以四边形BC1KM为平行四边形．所以MK∥BC1．在正方体ABCD－A1B1C1D1中，A1B1⊥平面BB1C1C，BC1⊂平面BB1C1C，所以A1B1⊥BC1．
因为MK∥BC1，所以A1B1⊥MK.因为四边形BB1C1C为正方形，所以BC1⊥B1C．所以MK⊥B1C．因为A1B1⊂平面A1B1C，B1C⊂平面A1B1C，A1B1∩B1C＝B1，所以MK⊥平面A1B1C．又因为MK⊂平面A1MK，所以平面A1B1C⊥平面A1MK.
【解题技巧】线面平行、垂直关系的证明问题的指导思想是线线、线面、面面关系的相互转化，本题(1)证明线面平行的思路是转化为证明线线平行，即证明AN与平面A1MK内的一条直线平行，从而得到AN∥平面A1MK；(2)证明面面垂直，可转化为平面A1MK内的直线MK垂直平面A1B1C1，要证线面垂直先证线线垂直，即只要证MK与A1B1及B1C垂直即可．
(2020年重庆模拟)如图，四棱锥P－ABCD的底面ABCD为矩形，PA⊥PD，其中M，N分别为PB，PC中点．(1)求证：MN∥平面PAD；(2)若平面PAD⊥底面ABCD，求证：PA⊥平面PCD．
证明：(1)因为M，N分别是PB，PC的中点，所以MN∥BC．又因为底面ABCD为矩形，所以BC∥AD．所以MN∥AD．又MN⊄平面PAD，AD⊂平面PAD，所以MN∥平面PAD．
(2)因为底面ABCD为矩形，所以CD⊥AD．又因为平面PAD⊥底面ABCD，平面PAD∩底面ABCD＝AD，且CD⊂平面ABCD，所以CD⊥平面PAD．又因为PA⊂平面PAD，所以PA⊥CD．又因为PA⊥PD，PD、CD⊂平面PCD，PD∩CD＝D，所以PA⊥平面PCD．