数学北师大版第七章 平行线的证明2 定义与命题作业课件ppt

这是一份数学北师大版第七章 平行线的证明2 定义与命题作业课件ppt，共20页。PPT课件主要包含了同角或等角的余角相等，等量代换，∠CAB，∠CAB＝70°等内容，欢迎下载使用。

1．“两条平行直线被第三条直线所截，同位角相等”这句话是( )A．定义 B．假命题C．公理 D．定理2．在证明过程中，可以用来作为推理根据的是( )A．命题、定义、公理 B．定理、定义、公理C．公理 D．定理、公理
3．下面关于公理和定理的联系说法不正确的是( )A．公理和定理都是真命题B．公理就是定理，定理也是公理C．公理和定理都可以作为推理论证的依据D．公理的正确性不需证明，定理的正确性需证明
4．某工程队，在修建高速公路时，有时需将弯曲的道路改直，根据什么公理可以说明这样做能缩短路程( )A．直线的公理B．直线的公理或线段最短公理C．线段最短公理D．平行公理
5．下列关于证明的说法正确的是( )A．证明是一种命题B．证明是一种推理过程C．证明是一种定理D．证明就是举例说明6．在下面的条件中，不能证明两个三角形全等的是( )A．三边对应相等B．有两角及一边对应相等C．有两边及一角对应相等D．两角及夹边对应相等
7．已知∠1＋∠2＝90°，∠3＋∠2＝90°，则∠1＝∠3，理由是______________________．
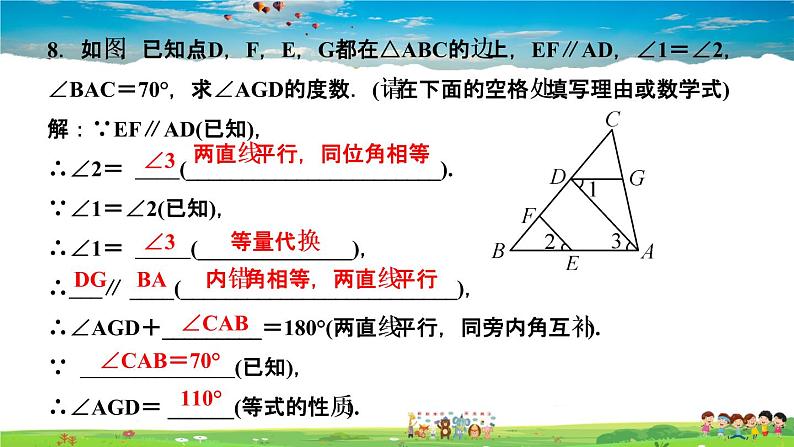
8．如图，已知点D，F，E，G都在△ABC的边上，EF∥AD，∠1＝∠2，∠BAC＝70°，求∠AGD的度数．(请在下面的空格处填写理由或数学式)解：∵EF∥AD(已知)，∴∠2＝ ____(_______________________).∵∠1＝∠2(已知)，∴∠1＝ _____(______________)，∴___∥ ____(_________________________)，∴∠AGD＋_________＝180°(两直线平行，同旁内角互补).∵ ______________(已知)，∴∠AGD＝ ______(等式的性质).
两直线平行，同位角相等
内错角相等，两直线平行
9．如图，已知a∥b，小亮把三角板的直角顶点放在直线b上．求证：∠1＋∠2＝90°.证明：∵a∥b(已知)，∴∠2＝∠3(两直线平行，同位角相等)，又∵∠BAC＝90°(已知)，∠1＋∠3＋∠BAC＝180°(平角的定义)，∴∠1＋∠2＝90°
10．如图，AC＝DC，BC＝EC，∠ACD＝∠BCE.求证：∠A＝∠D.
11．下列命题中是假命题的是( )A．推理的过程叫做证明B．定理都是命题C．命题都是公理D．公理都是命题12．“垂线段最短”有下列说法：①是命题；②是假命题；③是真命题；④是定理．其中正确的说法有( )A．①②③ B．①③④C．②③④ D．①②④
13．如图，在下列条件中，不能直接证明△ABD≌△ACD的是( )A.BD＝CD，AB＝ACB．∠ADB＝∠ADC，BD＝CDC．∠B＝∠C，∠BAD＝∠CADD．∠B＝∠C，BD＝DC
14．在下面的括号内，填上推理的根据：如图，已知AB∥CD，BE∥CF，求证：∠B＋∠C＝180°.证明：∵AB∥CD(已知)，∴∠B＝∠BGC(______________________)，又∵BE∥CF(已知)，∴∠BGC＋∠C＝180°(_________________________)，∴∠B＋∠C＝180°(____________).
两直线平行，内错角相等
两直线平行，同旁内角互补
15．如图，已知AD∥BC，∠1＝∠2，要证∠3＋∠4＝180°，请完善证明过程：证明：∵AD∥BC(已知)，∴∠1＝∠3(_____________________)，∵∠1＝∠2(已知)，∴∠2＝ ____(____________)，∴___∥ ____(______________________________)，∴∠3＋∠4＝180°(____________________________).
同位角相等，两直线平行
16．(武汉中考)如图，点C，F，E，B在一条直线上，∠CFD＝∠BEA，CE＝BF，DF＝AE，写出CD与AB的关系，并证明你的结论．
17．如图，点D，E在△ABC的边BC上，连接AD，AE.①AB＝AC；②AD＝AE；③BD＝CE.以此三个等式中的两个作为命题的题设，另一个作为命题的结论，构成三个命题：①②⇒③；①③⇒②；②③⇒①.(1)以上三个命题是真命题的为______________________________；(直接作答)(2)请选择一个真命题进行证明．(先写出所选命题，然后证明)
①②⇒③；①③⇒②；②③⇒①