【精品】五年级数学奥数思维训练提优卷（12）-全国通用版-含答案

这是一份【精品】五年级数学奥数思维训练提优卷（12）-全国通用版-含答案，共15页。

2. 如图，△ABC的面积为14平方厘米，DC=3DB，AE=ED．求阴影部分的面积．
3. 从一个长方体上截下一个体积是32立方厘米的长方体后，剩下的部分正好是棱长为4厘米的正方体.问原来这个长方体的表面积是多少平方厘米？
D
C
B
A
4. 如图，A、B是圆直径的两端点，亮亮在点A，明明在点B，相向而行.他们在C点第一次相遇，C点离A点100米；在D点第二次相遇，D点离B点80米.求圆的周长.
5. 假设旅客在检票进站前若干分钟就开始排队,每分钟来的旅客人数一样多,若同时开4个检票口,从开始检票口到等候检票的队伍消失,需30分钟；同时开5个检票口,20分钟后队伍消失。如果同时打开7个检票口,那么需要多少分钟队伍就消失?
6. 在同一个笼子中，有若干只鸡和兔，从笼子上看有40个头，从笼子下数有130只脚，那么这个笼子中装有兔、鸡各多少只？
7. 教室里有一只装苹果的纸箱,甲、乙、丙三人对箱中苹果数进行估计.甲说 ：“箱中至少有20个苹果.”乙说：“箱中苹果数不到20个.”丙说：“箱中最少有一个苹果.”我们知道这三个估计中只有一个估计是正确的.请问这只纸箱中究竟装了多少苹果?
8. 张,王,李,赵四位同学住在一个宿舍里．一天晚上,他们中间最晚回来的那位同学忘了关灯,第二天宿舍管理员查问谁回来的最晚,
(1)张说：我回来时,小李还没回来．
(2)王说：我回来时,小赵已经睡了,我也就睡了．
(3)李说：我进门时,小王正在床上．
(4)赵说：我回来就睡了,别的没注意．
他们说的都是实话,( )回来最晚．
9. 三个人打乒乓球,每场两人,输者退下换成另一人,这样继续下去,在甲打了9场,乙打了6场,丙最多打了( )场?
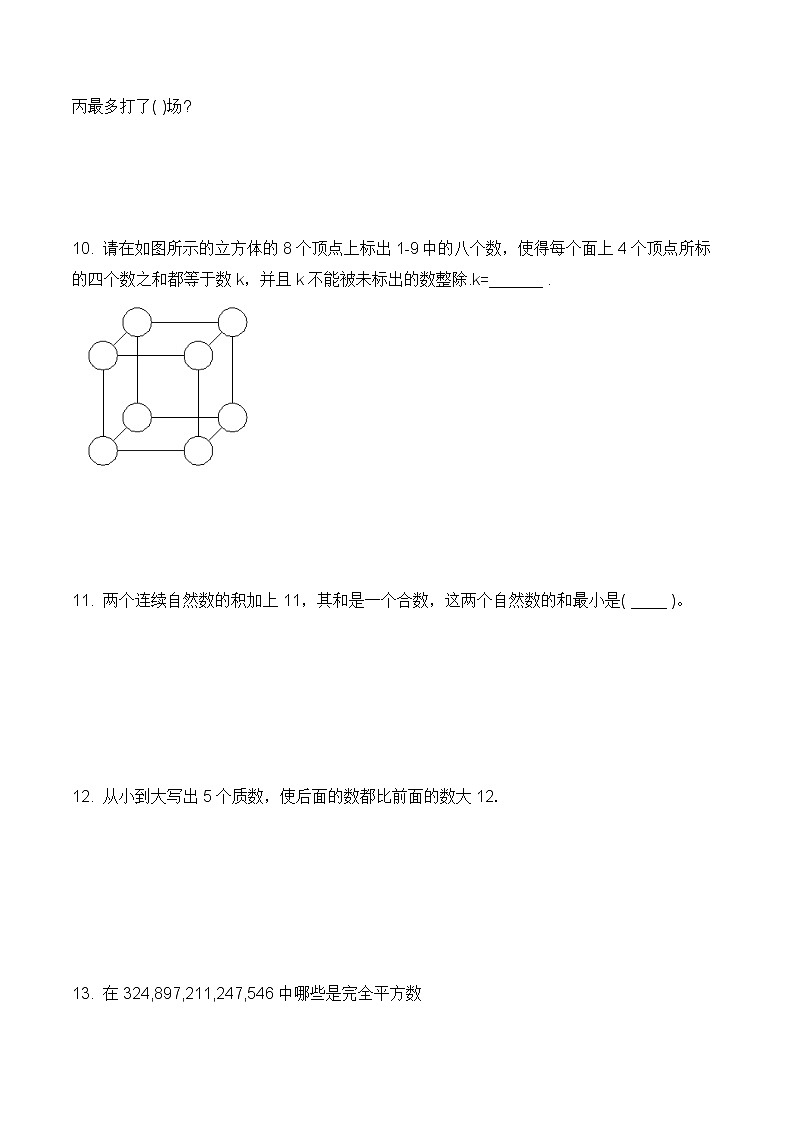
10. 请在如图所示的立方体的8个顶点上标出1-9中的八个数，使得每个面上4个顶点所标的四个数之和都等于数k，并且k不能被未标出的数整除.k=______ .
11. 两个连续自然数的积加上11，其和是一个合数，这两个自然数的和最小是( ____ )。
12. 从小到大写出5个质数，使后面的数都比前面的数大12．
13. 在324,897,211,247,546中哪些是完全平方数
14. 祖孙三人,孙子年龄与爷爷年龄之积是1512,而爷爷、父亲、孙子三人年龄之积是完全平方数,则父亲年龄是多少
15. 八个自然数排成一排，从第三个数开始，每个数都是它前面两个数之和，已知第五个数是7，那么第八个数是____ .
16. 三个连续的自然数后面两个数的积与前面两个数的积之差是114，那么这三个数中最小的数是____．
17. 在两位数10，11，…，98，99中，将每个被7除余2的数的个位与十位之间添加一个小数点，其余的数不变．问：经过这样改变之后，所有数的和是多少？
18. 在一个边长为1的正三角形内随意放置10个点，试说明其中至少有两个点之间的距离不超过.
19. 有三张数字卡片，分别写着1，2，3，同学们任意选取两张组成一个两位数．至少要几名同学参与才能保证其中有两人的卡片所组成的两位数相同？
20. 某商店有126箱苹果，每箱至少有120个苹果，至多有144个苹果．现将苹果个数相同的箱子算作一类．设其中箱子数最多的一类有n个箱子，则n的最小值为____．
参考答案
1. --------------------------------------------------------------------------
解析
“两块阴影部分的面积之和比三角形EFG的面积大10平方厘米”那么图中阴影部分面积加上中间梯形的面积(即这个平行四边形的面积)仍比三角形EFG的面积加上梯形的面积之和(即三角形BCE的面积)大10平方厘米，已知三角形BCE底和高分别为10厘米，8厘米，利用三角形的面积公式可以求出其面积，用其面积加上10，即可求出平行四边形的面积，已知平行四边形的底为BC=10厘米，用平行四边形的面积除以底即可求出它的高CF的长，如此解答即可.
答案
解：(10×8÷2+10)÷10
=(40+10)÷10
=50÷10
=5(厘米)故答案为：
答：CF的长是5厘米.
5厘米
点评
解答此题应明白：找出图中平行四边形和直角三角形的面积之间的关系，平行四边形的面积比直角三角形的面积大10平方厘米；先求出直角三角形的面积，进而求出平行四边形的面积，问题即可得解.
2. --------------------------------------------------------------------------
解：连接DF，
因为AE=DE，
所以S△AFE=S△DFE，S△ACE=S△DCE．
所以S△ACF=S△DCF．
又因为CD=3DB，
所以S△ACF=S△DCF=3S△BDF；
所以S△ABC=S△BDF×7=14，
故S△BDF=14÷7=2(平方厘米)．
S阴影=S△DCF=S△BDF×3=2×3=6(平方厘米)．
答：阴影部分的总面积是6平方厘米．
连接DF，根据高相等的三角形面积的比等于底边的比，得出△CDF与△BDF的关系．根据AE=DE，得出阴影△AEF与△DEF的面积相等．
图中的整个阴影的面积等于△CDF的面积．最后得出△CDF、△CAF、△BDF的关系，进而求解．
3. --------------------------------------------------------------------------
解析
根据题意，原长方体体积：32＋4×4×4＝96(立方厘米)，由于切去小长方体剩下正方体，所原长方体的底面是正方形，边长是有4厘米，因此底面积4×4＝16(平方厘米)，高96÷16＝6(厘米)，表面积就是：(4×6)×4＋4×4×2＝128(平方厘米).
答案
解：故答案为：
原长方体体积：
32＋4×4×4
＝32＋64
＝96(立方厘米)
原长方体的底面积：4×4＝16(平方厘米)
高：96÷16＝6(厘米)
表面积是：
(4×6)×4＋4×4×2
＝96＋32
＝128(平方厘米)
答：原来这个长方体的表面积是128平方厘米.
128平方厘米
点评
解答此题要仔细审题，理解题意，理清思路，准确计算.关键是根据“剩下的部分正好是棱长为4厘米的正方体”找出原来长方体的底面是正方形.熟记：正方体的体积＝棱长×棱长×棱长，长方体的体积＝长×宽×高，高＝长方体的体积÷底面积，长方体的表面积＝(长×宽＋长×高＋宽×高)×2.
4. --------------------------------------------------------------------------
解析
圆的周长为C，第一次相遇时两人共走了0.5 C，第二次相遇时两人共走了1.5 C，即第二次相遇时两人共走的路程是第一次相遇时的三倍，而第一次相遇时亮亮走了100米，故第二次相遇时亮亮共走了100×3=300米，而A到D为C÷2+80 米．故 C÷2+80=300，得C=440米，即圆的周长为440米.
答案
解：（100×2-80+100）×2，
=220×2，
=440(米)；故答案为：
440米
点评
此题属于环形跑道问题，可以把它看作相遇问题来处理．第二次相遇时亮亮共走了“C÷2+80=300”是解题的关键，学生在做题时要注意分析.
5. --------------------------------------------------------------------------
假设检票时每分钟有x个旅客过来检票,检票前若干分钟排了z个旅客,检票时每个检票口每分钟检票y个旅客,假设开7个检票口需要t分钟队伍消失,那么有：
4个检票口情况：z+30x=4×30y...等式1；
5个检票口情况：z+20x=5×20y...等式2；
7个检票口情况：z+tx =7×ty.等式3；
由等式1和等式2左右两边相减得：x=2y...等式4；
将等式4带入等式1或者2任意一个中得：z=60y...等式5；
由等式3得：t=z÷(7y-x)...等式6；
将等式4和5带入6,得：t=12
6. --------------------------------------------------------------------------
7. --------------------------------------------------------------------------
设纸箱中有x个苹果
甲：x≥20
乙：x＜20
丙：x≥1
丙的答案既可以包含于甲，又可以包含于乙
假设甲是正确的
那么丙也一定是正确的，所以甲不能是正确的；（例如，x=20）
如果乙是正确的
那么丙可以是正确的（例如x=19或者x=1），所以，只有丙不成立的时候（即x