






还剩10页未读,
继续阅读
初中冀教版第24章 一元二次方程24.3 一元二次方程根与系数的关系图文课件ppt
展开
这是一份初中冀教版第24章 一元二次方程24.3 一元二次方程根与系数的关系图文课件ppt,共18页。PPT课件主要包含了数学名人传韦达,本节课你学到了什么,有什么收获,谢谢观看等内容,欢迎下载使用。
1、经历一元二次方程根与系数的关系的探究过程,体会探究过程中体现的化归思想。2、了解一元二次方程根与系数的关系,能用符号表示根与系数的关系。3、应用一元二次方程中根与系数的关系,解决一些简单的问题。
2.一元二次方程的根的情况怎样确定?
1.一元二次方程的求根公式是什么?
想一想:方程的两个根x1 , x2与系数a,b,c还有其它关系吗?
一元二次方程根与系数的关系
试求一个一元二次方程,使它的两个根分别为 ①2和3;②-4和7;③3和-8;④-5和-2
问题1:从求这些方程的过程中你发现根与各项系数之间有什么关系?
总结:如果一元二次方程x2+px+q=0有两个根是x1 , x2 那么有x1+ x2= -p, x1 •x2= q
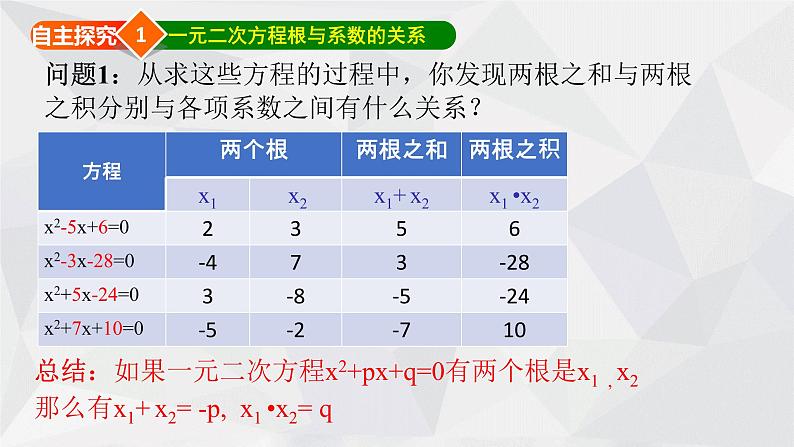
问题1:从求这些方程的过程中,你发现两根之和与两根之积分别与各项系数之间有什么关系?
结论:如果一元二次方程x2+px+q=0有两个根是x1 , x2 那么有x1+ x2= -p, x1 •x2= q
猜想1:2x2-5x+3=0( x1= ,x2=1; x1+ x2= , x1 •x2= ),这个方程的两根之和,两根之积分别与各项系数之间有什么关系?
猜想2:对于一元二次方程的一般式: 是否也有这样的结论? 若设它的两个根分别是x1 , x2,那么有x1+ x2= __________, x1 • x2= __________.
如果一元二次方程 的两个根分别是 、 ,那么:
这就是一元二次方程根与系数的关系,也叫韦达定理。
16世纪法国最杰出的数学家韦达发现 代数方程的根与系数之间有这种关系,因此,人们把这个关系称为韦达定理。数学原本只是韦达的业余爱好,但就是这个业余爱好,使他取得了伟大的成就。韦达是第一个有意识地和系统地使用字母表示数的人,并且对数学符号进行了很多改进。是他确定了符号代数的原理与方法,使当时的代数学系统化并且把代数学作为解析的方法使用。因此,他获得了“代数学之父”之称。
韦达(1540-1603)
例1 根据一元二次方程的根与系数的关系,求下列方程两个根的和与积: (1) x2-3x-8=0 (3) 2x2+5x=0 (5) 3x2=1 (2) 3x2+4x-7=0; (4) 3x2-2x=-2
1、一元二次方程x2+4x-3=0的两根为x1,x2,则x1·x2的值是( )A.4 B.-4 C.3 D.-32、已知x1、x2是方程x2+3x-1=0的两个实数根,那么下列结论正确的是( )A.x1+x2=-1 B.x1+x2=-3 C.x1+x2=1 D.x1+x2=3
3、已知关于x的一元二次方程x2-x+4k=0有两个相等的实数根.(1)求k的值.(2)求两个根的和与积.
4、(1)已知方程x2+(k-1)x+3=0的两根之和为6 , 求k的值及方程的两根.(2)已知方程x2+(k-1)x+ k2 =0的两根之积为1 , 求k的值.
请同学们谈谈本节课的收获与体会
1、必做P46 练习1、习题A组 1 2、选做P46 习题B1
1、经历一元二次方程根与系数的关系的探究过程,体会探究过程中体现的化归思想。2、了解一元二次方程根与系数的关系,能用符号表示根与系数的关系。3、应用一元二次方程中根与系数的关系,解决一些简单的问题。
2.一元二次方程的根的情况怎样确定?
1.一元二次方程的求根公式是什么?
想一想:方程的两个根x1 , x2与系数a,b,c还有其它关系吗?
一元二次方程根与系数的关系
试求一个一元二次方程,使它的两个根分别为 ①2和3;②-4和7;③3和-8;④-5和-2
问题1:从求这些方程的过程中你发现根与各项系数之间有什么关系?
总结:如果一元二次方程x2+px+q=0有两个根是x1 , x2 那么有x1+ x2= -p, x1 •x2= q
问题1:从求这些方程的过程中,你发现两根之和与两根之积分别与各项系数之间有什么关系?
结论:如果一元二次方程x2+px+q=0有两个根是x1 , x2 那么有x1+ x2= -p, x1 •x2= q
猜想1:2x2-5x+3=0( x1= ,x2=1; x1+ x2= , x1 •x2= ),这个方程的两根之和,两根之积分别与各项系数之间有什么关系?
猜想2:对于一元二次方程的一般式: 是否也有这样的结论? 若设它的两个根分别是x1 , x2,那么有x1+ x2= __________, x1 • x2= __________.
如果一元二次方程 的两个根分别是 、 ,那么:
这就是一元二次方程根与系数的关系,也叫韦达定理。
16世纪法国最杰出的数学家韦达发现 代数方程的根与系数之间有这种关系,因此,人们把这个关系称为韦达定理。数学原本只是韦达的业余爱好,但就是这个业余爱好,使他取得了伟大的成就。韦达是第一个有意识地和系统地使用字母表示数的人,并且对数学符号进行了很多改进。是他确定了符号代数的原理与方法,使当时的代数学系统化并且把代数学作为解析的方法使用。因此,他获得了“代数学之父”之称。
韦达(1540-1603)
例1 根据一元二次方程的根与系数的关系,求下列方程两个根的和与积: (1) x2-3x-8=0 (3) 2x2+5x=0 (5) 3x2=1 (2) 3x2+4x-7=0; (4) 3x2-2x=-2
1、一元二次方程x2+4x-3=0的两根为x1,x2,则x1·x2的值是( )A.4 B.-4 C.3 D.-32、已知x1、x2是方程x2+3x-1=0的两个实数根,那么下列结论正确的是( )A.x1+x2=-1 B.x1+x2=-3 C.x1+x2=1 D.x1+x2=3
3、已知关于x的一元二次方程x2-x+4k=0有两个相等的实数根.(1)求k的值.(2)求两个根的和与积.
4、(1)已知方程x2+(k-1)x+3=0的两根之和为6 , 求k的值及方程的两根.(2)已知方程x2+(k-1)x+ k2 =0的两根之积为1 , 求k的值.
请同学们谈谈本节课的收获与体会
1、必做P46 练习1、习题A组 1 2、选做P46 习题B1













