初中数学冀教版九年级上册24.2 解一元二次方程评课课件ppt

这是一份初中数学冀教版九年级上册24.2 解一元二次方程评课课件ppt，共16页。PPT课件主要包含了复习引入，想一想，简记歌诀等内容，欢迎下载使用。

1.已学过的一元二次方程解法有哪些？
2.因式分解的方法有哪些？
1.做一做：将下列式子分解因式（1）x2-3x =（2）x2-4 =（3）x2-3x+2 =
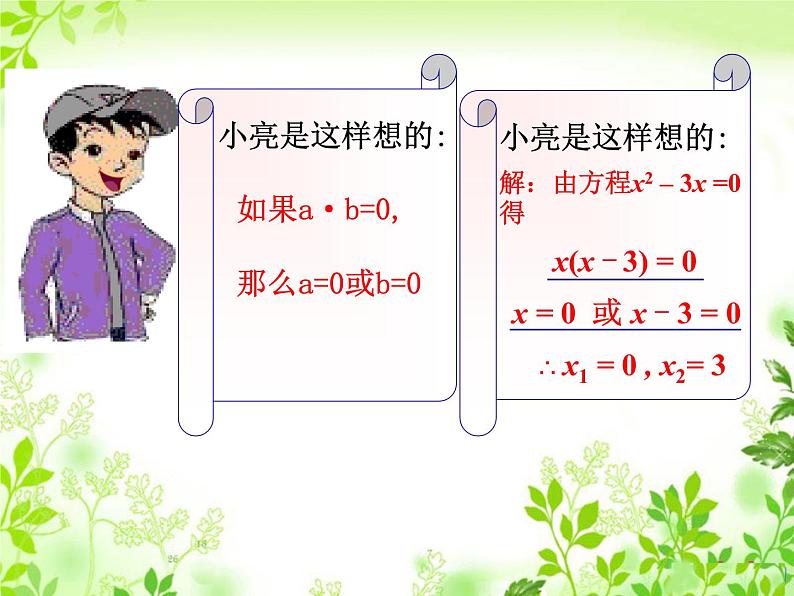
(1)x(x-3)=0
(2)(x+2)(x-2)=0
x1=0 , x2=3
x1=-2 , x2=2
2.猜一猜：下列方程的解
(3)(x-1)(x-2)=0
x1=1 , x2=2
方程x2 – 3x=0变形为x 2=3x 两边同时约去x，得x=3所以这个数就是3
当一元二次方程的一边是0,而另一边易于分解成两个一次因式的乘积时,我们就可以用分解因式的方法求解.这种用分解因式解一元二次方程的方法称为因式分解法.
1.用因式分解法的条件是: 方程右边等于零,而左边易分解. 2.理论依据是“如果a·b=0,那么a=0或b=0.”
例1：用因式分解法解下列方程： （1）5x2 = 4x ; （2） x (x – 2)= x – 2 .
解：原方程可变形为5x2 – 4x = 0x (5x – 4) = 0x = 0 或 5x – 4 = 0∴ x1 = 0 , x2= .
解：原方程可变形为 x (x – 2) – (x – 2) = 0 (x – 2) (x – 1) = 0 x – 2 = 0 或 x – 1 = 0 ∴ x1 = 2 , x2= 1.
（1）对于一元二次方程( x - p ) ( x - q ) =0,那么它的两个实数根分别为 .（2）对于已知一元二次方程的两个实数根为p，q，那么这个一元二次方程可以写成 的形式.
( x - p ) ( x - q ) =0
x1 = p , x2= q
1.快速说出下列方程的解（1） (x - 2)(x - 3) = 0; x1 =（ ）, x2 = ( ).（2）(2x + 3)(x - 4) = 0; x1 =（ ）, x2 = ( )（3） (4x - 1)(5x + 7) = 0; x1 =（ ）, x2= ( ).2.将下面一元二次方程补充完整.（1） (x - )(3x - 4) = 0; x1= 2 , x2= .（2）（2x - ）(x + 3) = 0; x1= , x2= - 3.（3）（3x +____）(x + ) = 0; x1= , x2= - 5.
例2： 用因式分解法解方程：（1）(x + 1)2 -25 = 0； （2）x2 – 7x= 8
解：原方程可变形为 x2 - 7x - 8 =0 (x + 1) (x - 8) =0 x + 1 = 0 或 x - 8 = 0
∴ x1 =- 1 , x2= 8
∴ x1 =- 6 , x2=4
(x + 6) (x - 4) =0 x + 6 = 0 或 x - 4 = 0
方程 (x + 1) (x - 1) = 8 的两个根为 x1 =-1 , x2= 1. 对不对？
解：原方程可变形为 x2 - 1 = 8 x2 - 9 = 0(x + 3) (x - 3)= 0x + 3 = 0 或 x - 3 = 0∴ x1 =- 3 , x2= 3
用因式分解法解下列方程：（1） ( 2x + 3 ) 2 = 4 (2x + 3) ; （2）(2x + 3) 2=(x - 2) 2
解：原方程可变形为（2x + 3）2 - 4 (2x + 3) = 0 (2x + 3) (2x + 3 - 4) = 0 (2x + 3) (2x - 1) = 0 2x + 3 = 0 或 2x - 1 = 0
解：原方程可变形为 (2x + 3 ) 2 - (x - 2) 2 = 0(2x + 3 + x - 2) (2x + 3 - x + 2) = 0 (3x + 1)(x + 5) = 0 3x + 1 = 0 或 x + 5 = 0
（3）2(x – 3)2 = x 2 – 9 ; （4）(2 – y)2 + y2 = 4.
解：原方程可变形为 2(x – 3)2 – (x2 – 9) = 0 2(x – 3)2 – (x + 3)(x – 3) = 0( x – 3) (2x – 6 – x – 3) = 0.( x – 3) (x – 9) = 0.x – 3 = 0 或 x – 9 = 0. ∴ x1 = 3 , x2 = 9.
解：原方程可变形为 (2– y )2 + (y2 – 4) = 0 (y – 2)2 + (y+2)(y – 2) = 0( y – 2) (y – 2 +y +2) = 02y( y – 2) = 0y( y – 2) = 0y = 0 或 y – 2 = 0 ∴ y1 = 0 , y2 = 2
1.用因式分解法解一元二次方程理论依据： “如果a·b=0,那么a=0或b=0.”
右化零　　左分解两方程　　各求解
解一元二次方程的方法：
（1）直接开平方法（2）配方法 　（3）公式法 （4）因式分解法