必修13.1.2用二分法求方程的近似解评课ppt课件

这是一份必修13.1.2用二分法求方程的近似解评课ppt课件，共36页。PPT课件主要包含了知识回顾，如何找出这个零点，生活中的二分法，资料查询，新知探究，二分法的定义，概念拓展实践探究，借助图像等内容，欢迎下载使用。

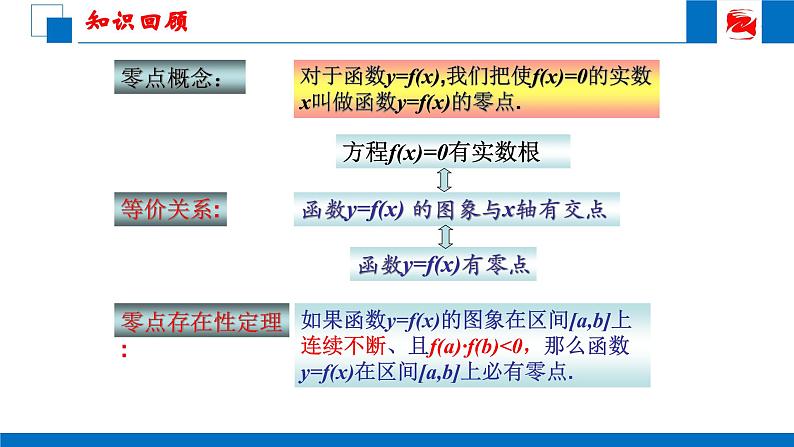
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
方程f(x)=0有实数根
函数y=f(x) 的图象与x轴有交点
函数y=f(x)有零点
如果函数y=f(x)的图象在区间[a,b]上连续不断、且f(a)·f(b)<0，那么函数y=f(x)在区间[a,b]上必有零点.
放在银行门口电动车在早7：00到19:00，12小时内被盗，正好被监控器拍到。请你化身为小侦探，用最快的方法检索监控视频，将小偷逃跑时间提供给警察。
这种解决问题的方法，就是我们今天要学的二分法。
查找线路电线、水管、气管等管道线路故障
定义：每次取中点，将区间一分为二，再经比较，按需要留下其中一个小区间的方法叫二分法，也叫对分法，常用于：
是方程求根的常用方法！
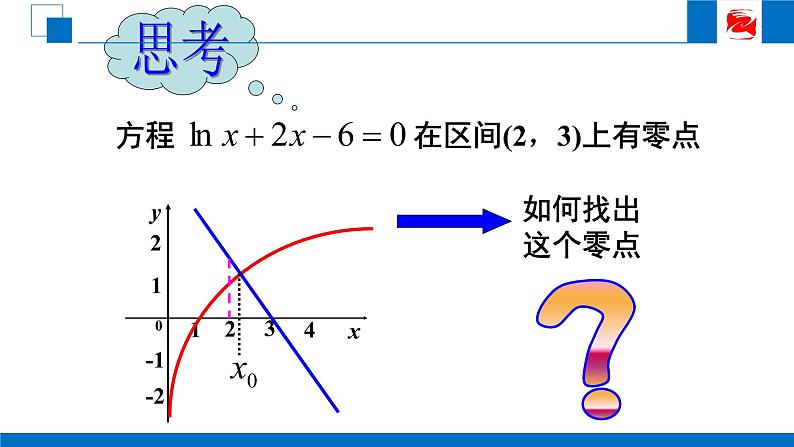
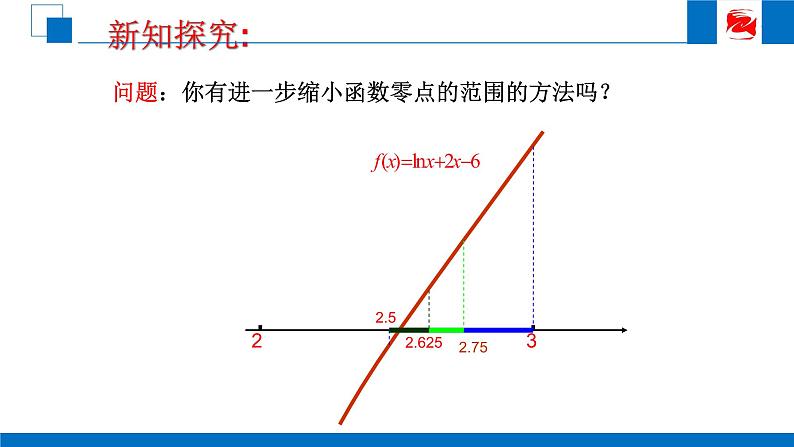
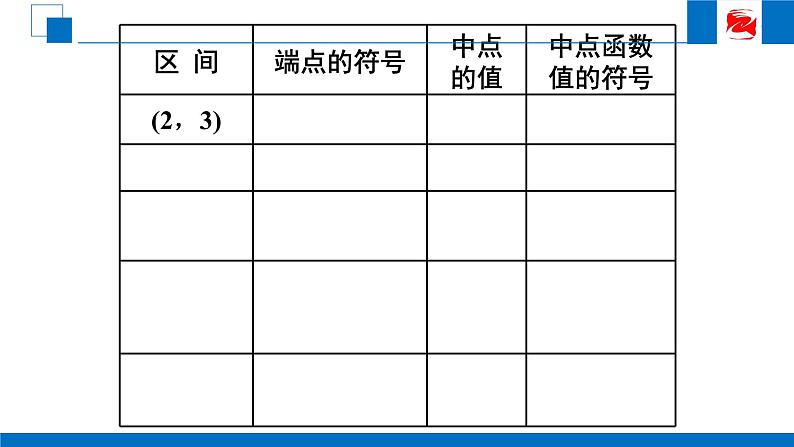
问题：你有进一步缩小函数零点的范围的方法吗？
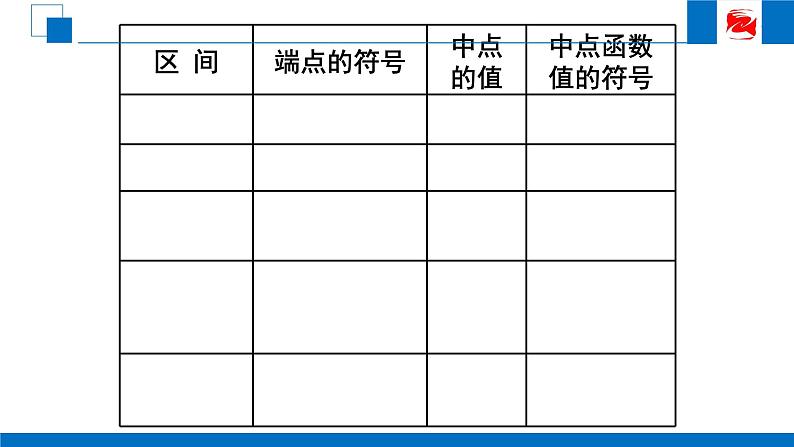
f(2)<0， f(3)>0
f(2)<0，f(3)>0
f(2)<0, f(3)>0
f(2.5)<0, f(3)>0
(2.5, 2.75)
f(2.5)<0,f(2.75)>0
(2.5, 2.625)
f(2.5)<0, f(2.625)>0
f(2.5625)>0
(2.5, 2.5625)
f(2.5)<0,f( 2.5625)>0
f(2.53125)<0
上述求函数零点近似值的方法叫做二分法，那么二分法的基本思想是什么？
对于在区间[a，b]上连续不断且f(a)·f(b)<0的函数y=f(x)，通过不断地把函数f(x)的零点所在的区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点近似值的方法叫做二分法.
对于在区间[a，b]上连续不断且 f(a).f(b)<0的函数y=f(x)，通过不断的把函数f(x)的零点所在的区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点近似值的方法叫做二分法.
知识探究（二）:用二分法求函数零点近似值的步骤:
思考1:求函数f(x)的零点近似值第一步应做什么？
思考2:为了缩小零点所在区间的范围，接下来应做什么？
确定区间[a,b]，使 f(a)f(b)<0.
求区间的中点c，并计算f(c)的值.
思考2:若f(c)=0说明什么？ 若f(a)·f(c)<0或f(c)·f(b)<0 ，则分别说明什么？
若f(c)=0 ，则c就是函数的零点；
若f(a)·f(c)<0 ，则零点x0∈(a,c)；
若f(c)·f(b)<0 ，则零点x0∈(c,b).
思考3:若给定精确度ε，如何选取近似值？
当|m-n|<ε时，区间[m，n]内的任意一个值都是函数零点的近似值.
思考4：对下列图象中的函数，能否用二分法求函数零点的近似值？为什么？
注意：二分法仅对函数的变号零点适用，对函数的不变号零点不适用.
练习:下列函数图像与x轴均有交点，但不宜用二分法求交点横坐标的是( )
例1:求方程x2-2x-1=0的一个正的近似解 (精确度0.1).
f(2)<0 , f(3)>0
(2.375,2.5)
(2.375,2.4375)
f(2)<0 , f(2.5)>0
f(2.25)<0 , f(2.5)>0
f(2.375)<0 , f(2.5)>0
f(2.375)<0 , f(2.4375)>0
f(2.4375)>0