数学必修 第二册5.4 统计与概率的应用课文内容课件ppt

这是一份数学必修 第二册5.4 统计与概率的应用课文内容课件ppt，共16页。
1. 了解统计与概率在实际生活中应用的广泛性.2.会用统计和概率的有关知识解决实际问题.3.能用统计和概率的方法与思想分析问题.
重点：统计与概率知识的应用.难点：利用统计和概率知识解决实际问题..
一.本章所学主要内容
8.事件的独立性P（AB）＝P（A）P（B）.
三.估计盒子中玻璃球的个数
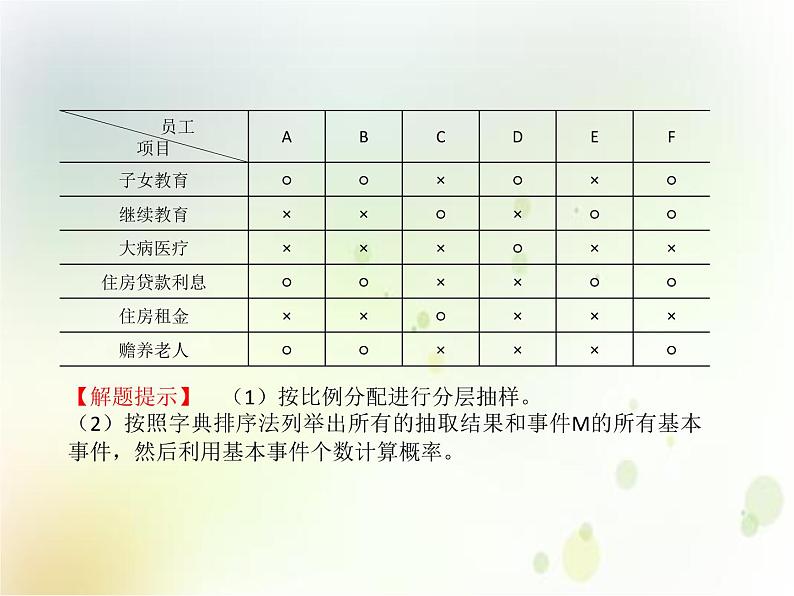
题型一　随机抽样与概率的综合问题【例1】2019·天津卷］2019年，我国施行个人所得税专项附加扣除办法，涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72，108，120人，现采用分层抽样的方法，从该单位上述员工中抽取25人调查专项附加扣除的享受情况.（1）应从老、中、青员工中分别抽取多少人？（2）抽取的25人中，享受至少两项专项附加扣除的员工有6人，分别记为A，B，C，D，E，F.享受情况如下表，其中“○”表示享受，“×”表示不享受.现从这6人中随机抽取2人接受采访.①试用所给字母列举出所有可能的抽取结果；②设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”，求事件M发生的概率.
【解题提示】　（1）按比例分配进行分层抽样。（2）按照字典排序法列举出所有的抽取结果和事件M的所有基本事件，然后利用基本事件个数计算概率。
【归纳总结】在高考中所考查的概率解答题，一般都是确定好基本事件空间之后，对基本事件个数用列举法列举，列举时无论使用什么形式，都要注意应用字典排序法才能不重不漏，因为只要正确列举出来，概率的计算就很简单了。
【归纳总结】概率问题常常与频率分布综合考查，求解的方法是利用频率分布求出样本空间中基本事件个数，和所求事件含有多少个基本事件，最后利用古典概型的概率公式求出概率。解题关键是读图识图能力。
解：（1）由频率分布直方图可知,月均用水量在［0，0.5）的频率为0.08×0.5＝0.04，同理，在［0.5，1），［1.5，2），［2，2.5），［3，3.5），［3.5，4），［4，4.5］组的频率分别为0.08，0.21，0.25，0.06，0.04，0.02.由1-（0.04+0.08+0.21+0.25+0.06+0.04+0.02）＝0.5×a+0.5×a，解得a=0.30.（2）由（1）知，该市100位居民中月均用水量不低于3吨的频率为0.06+0.04+0.02=0.12.由以上样本的频率分布，可以估计30万居民中月均用水量不低于3吨的人数为300 000×0.12＝36 000.（3）设中位数为x吨.因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25＝0.73>0.5，而前4组的频率之和为0.04+0.08+0.15+0.21＝0.48