2020-2021学年第一章 全等三角形综合与测试练习

这是一份2020-2021学年第一章 全等三角形综合与测试练习，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
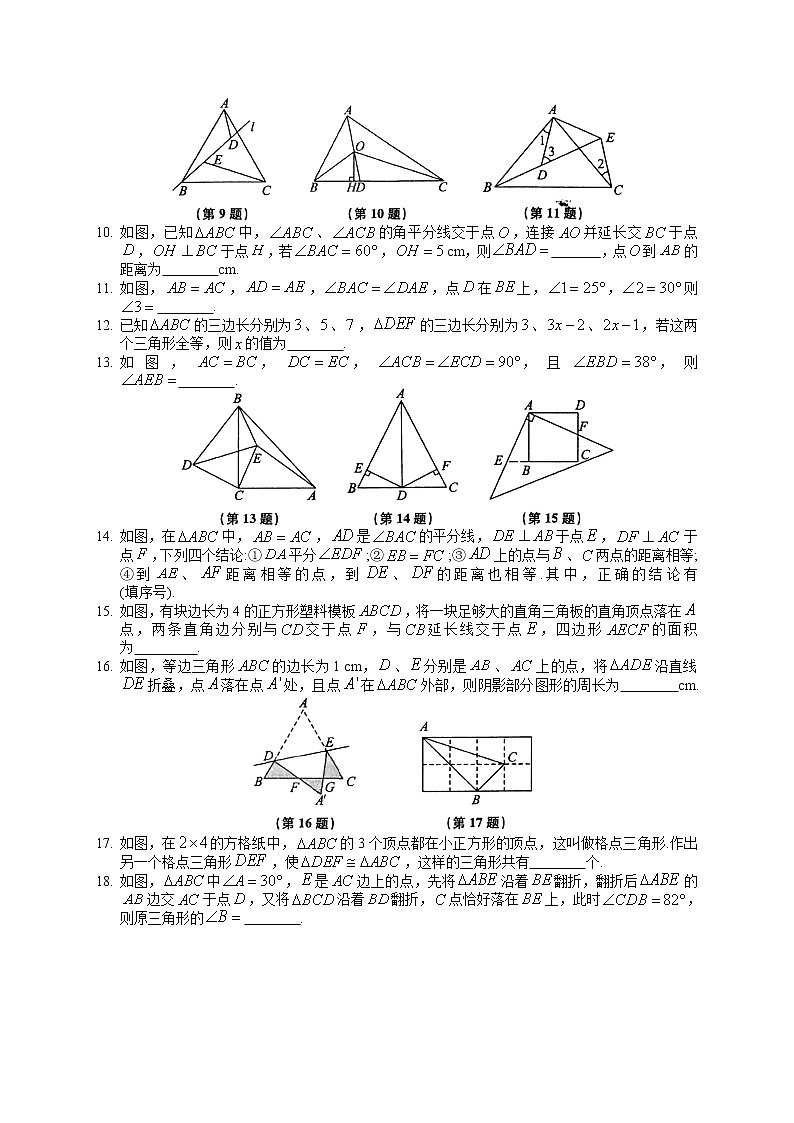
2021-2022学年度苏科版八年级数学上册第一章全等三角形单元强化训练卷（B）姓名               班级              座号         成绩            一、选择题 (每题3分，共24分)1．不能使两个直角三角形全等的条件是(    )    A.一条直角边和它的对角对应相等  B.斜边和一条直角边对应相等    C.斜边和一锐角对应相等          D.两个锐角对应相等2． 如图，于点，且，，则，则等于(    )A 25°            B. 27°            C. 30°            D. 45°如图，，下列条件中不能判断的是(   )    A.                         B.     C.                         D. 如图，在正方形中，连接，是的中点，若、是边上的两点，连接、，并分别延长交边于两点、，则图中的全等三角形共有(    )    A. 2对            B. 3对            C. 4对            D. 5对如图，在长方形中()，是上一点，且，，垂足为.在下列结论中，不一定正确的是(    )A.                    B. C.                          D. 如图，将绕着点顺时针旋转50后得到.若，，则的度数是(    )    A. 110°           B. 80°           C. 40°            D. 30°如图，中，，，，则下列结论正确的是(    )    A.                   B.     C.                   D. 如图，，，，，则(    )A.                       B.C.                    D.二、填空题(每题2分，共20分)如图，直线经过等边三角形的顶点，在上取点、，使. 若cm，cm，则        cm如图，已知中，、的角平分线交于点，连接并延长交于点，于点，若，cm，则       ，点到的距离为        cm.如图，，，，点在上，，则        .已知的三边长分别为、、，的三边长分别为、、，若这两个三角形全等，则的值为        .如图，，，，且，则        .如图，在中，，是的平分线，于点，于点，下列四个结论:①平分;②;③上的点与、两点的距离相等;④到、距离相等的点，到、的距离也相等.其中，正确的结论有               (填序号).如图，有块边长为4的正方形塑料模板，将一块足够大的直角三角板的直角顶点落在点，两条直角边分别与交于点，与延长线交于点，四边形的面积为         .如图，等边三角形的边长为1 cm，、分别是、上的点，将沿直线折叠，点落在点处，且点在外部，则阴影部分图形的周长为        cm.如图，在的方格纸中，的3个顶点都在小正方形的顶点，这叫做格点三角形.作出另一个格点三角形，使，这样的三角形共有        个.如图，中，是边上的点，先将沿着翻折，翻折后的边交于点，又将沿着翻折，点恰好落在上，此时，则原三角形的        .三、解答题(共56分)(6分)如图，点、、、在直线上(点、之间的距离不能直接测量)，点、在异侧，测得、、.(1)求证: .(2)指出图中所有平行的线段，并说明理由.  (6分)如图，在中，，点、分别在、上，，连接，将线段绕点按顺时针方向旋转90°后得，连接.    (1)补充完成图形.    (2)若，求证: .  (6分)如图，已知: ，是的中点，平分.求证:    (1) 平分.    (2) .  (6分)如图，在正方形中，点在边上，于点，于点.    (1)求证:.    (2)在不添加任何辅助线的情况下，请直接写出图中四对线段，使每对中较长线段与较短线段长度的差等于的长.  (8分)如图，已知为等腰直角三角形内一点，，为延长线上的一点，且.(1)求证:平分.(2)若点在上，且，求证:.  24.(8分)如果将四根木条首尾相连，在相连处用螺钉连接，就能构成一个平面图形.    (1)若固定三根木条、、不动，cm，cm，如图，量得第四根木条cm，判断此时与是否相等，并说明理由.    (2)若固定一根木条不动，cm，量得木条cm，如果木条、 的长度不变，当点移到的延长线上时，点也在的延长线上;当点移到的延长线上时，点、、能构成周长为cm的三角形，求出木条、的长度.(8分)    (1)如图①，以的边、为边分别向外作正方形和正方形，连接，试判断与面积之间的关系，并说明理由.    (2)园林小路，曲径通幽，如图②所示，小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是m2，内圈的所有三角形的面积之和是m2，这条小路一共占地多少平方米?  (8分)如图，在四边形中，，，，点从点出发，以每秒1个单位长度的速度沿向点匀速移动，点从点出发，以每秒3个单位长度的速度沿作匀速移动，点从点出发沿向点移动，三个点同时出发，当有一个点到达终点时，其余两点也随之停止运动，假设移动时间为ts.    (1)试证明:.    (2)在移动过程中，小明发现有与全等的情况出现，请你探究这样的情况会出现几次?并分别求出此时的移动时间和点的移动距离.参考答案一、1. D   2. B   3. C   4. C   5. B   6. B   7. A   8. D二、9.    10.  11.  12.  13.      14.①②③④15.  16.   17. 18.三、19.略20. (1)略(2)由旋转的性质得，，所以因为所以所以因为所以所以在和，所以所以21. (1)过作于点因为平分，，所以又因为所以因为，所以平分AM(2)因为所以又因为，所以同理:因为所以22. (1)因为正方形所以，即因为所以所以因为，所以所以所以   (2)①②③④23. (1)因为是等腰直角三角形所以因为所以所以所以点在的垂直平分线上因为所以点也在的垂直平分线上即直线是的垂直平分线所以所以所以所以即平分 ( 2 )连接因为，且所以是等边三角形所以，因为，所以又因为所以在与中所以所以24. (1)相等.理由：连接在和中，所以所以  (2)设，当点在点右侧时解得当点在点左侧时解得此时不合题意所以cm，cm.25. (1)与面积相等理由:过点作于点，过点作交延长线于点则因为四边形和四边形都是正方形所以，，因为所以因为所以在和中所以所以因为，所以 (2)由(1)知外圈的所有三角形的面积之和等于内圈的所有三角形的面积之和.所以这条小路的面积为m2.26. (1)在和中，所以所以所以 (2)设点的移动距离为，当与全等时有所以，或，当点由点到点即时，则有解得或解得(舍去)当点由点到点即时，有解得或解得综上可知共会出现3次，移动的时间分别为2s、4s、5s，移动的距离分别为6、6、5