

2021-2022学年度北师大版九年级数学上册第二次月考模拟试卷(含解析)
展开
这是一份2021-2022学年度北师大版九年级数学上册第二次月考模拟试卷(含解析),共25页。试卷主要包含了选择题,四象限,解答题等内容,欢迎下载使用。
2021-2022学年度北师大版九年级数学上册第二次月考模拟试卷
一、选择题(每小题3分,共30分)
1.在Rt△ABC中,∠C=90°,tanA=,则cosA等于( )
A. B. C. D.
2.把二次函数y=﹣x2﹣2x+3配方化为y=a(x﹣h)2+k形式是( )
A.y=﹣(x﹣1)2﹣4 B.y=﹣(x+1)2+4
C.y=﹣(x﹣1)2+3 D.y=﹣(x+1)2﹣3
3.对于反比例函数y=,下列判断正确的是( )
A.图象经过点(﹣1,3)
B.图象在第二、四象限
C.不论x为何值,y>0
D.图象所在的第一象限内,y随x的增大而减小
4.矩形具有但菱形不一定具有的性质是( )
A.对边平行且相等 B.对角相等、邻角互补
C.对角线相等 D.对角线互相垂直
5.在平面直角坐标系中,将函数y=﹣2x2的图象先向右平移1个单位长度,再向上平移5个单位长度,得到图象的函数解析式是( )
A.y=﹣2(x+1)2+5 B.y=﹣2(x﹣1)2+5
C.y=﹣2(x+1)2﹣5 D.y=﹣2(x﹣1)2﹣5
6.如图,已知∠1=∠2,则添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )
A. B. C.∠B=∠ADE D.∠C=∠E
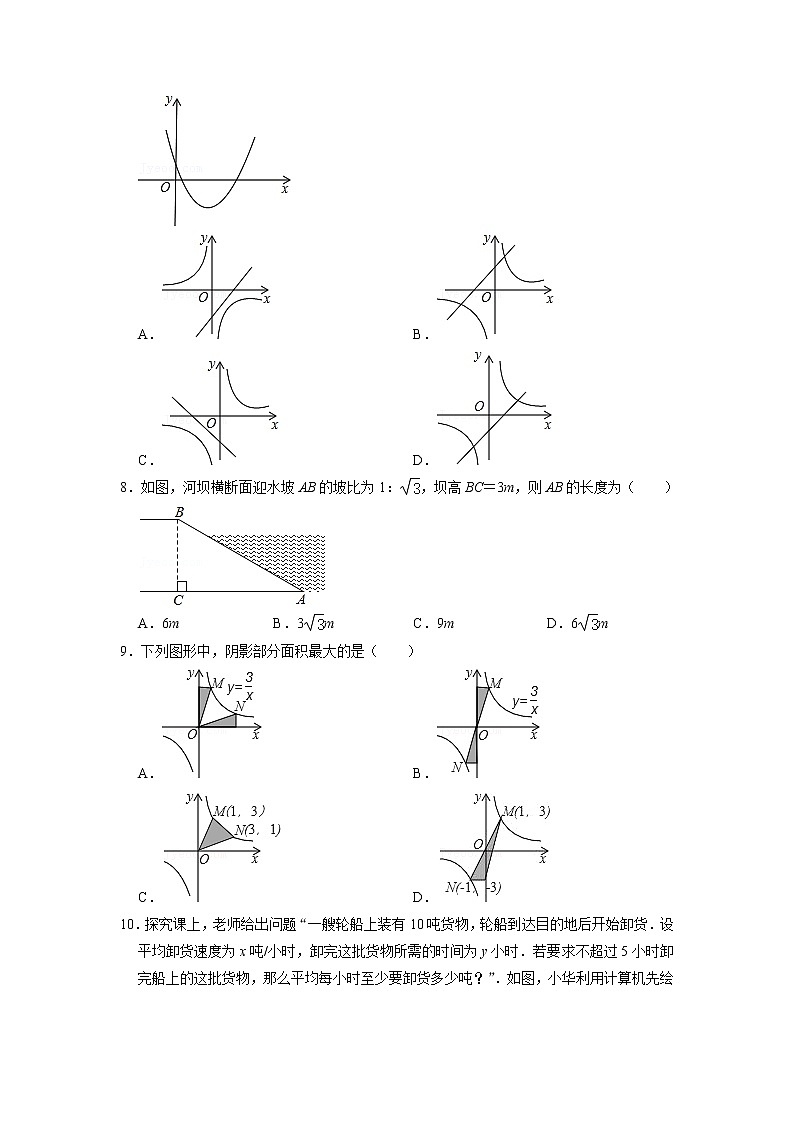
7.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b和反比例函数y=在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
8.如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=3m,则AB的长度为( )
A.6m B.3m C.9m D.6m
9.下列图形中,阴影部分面积最大的是( )
A. B.
C. D.
10.探究课上,老师给出问题“一艘轮船上装有10吨货物,轮船到达目的地后开始卸货.设平均卸货速度为x吨/小时,卸完这批货物所需的时间为y小时.若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?”.如图,小华利用计算机先绘制出反比例函数的图象,并通过观察图象发现:当0<y≤5时,x≥2.所以小华得出此题答案为:平均每小时至少要卸货2吨.小华的上述方法体现的数学思想是( )
A.公理化 B.数形结合
C.分类讨论 D.由特殊到一般
二、填空题(每题3分,共15分)
11.如图,在点A处测得点B处的仰角是 .(用“∠1,∠2,∠3或∠4”表示)
12.已知二次函数y=ax2+bx+c自变量x与函数值y之间满足右面表格中的数量关系:由表可知,该二次函数的对称轴是 .
x
2
4
5
y
0.2
0.2
2
13.如图,一次函数的图象分别交x轴,y轴于N,A两点,与反比例函数在第一象限的图象交于点B,若点N是线段AB的中点,则k的值为 .
14.如图,在矩形ABCD中,,将矩形ABCD绕着点A逆时针旋转一定角度得到矩形AB′C′D′,若点B′落在边CD上,则∠DAD′= °.
15.已知二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点B的坐标为(1,0),其图象如图所示,下列结论:①abc<0;②2a﹣b=0;③当y>0时,x>1;④3b+2c>0;⑤当x<0时,y随x的增大而减小;其中正确的有 .(只填序号)
三、解答题(共75分)
16.(1)解下列方程:x2﹣1=2(x+1);
(2)计算:+sin60°⋅cos45°﹣tan30°.
17. 2020年国庆小长假,小华一家计划利用假期的时间出去旅游,他们收集了很多旅游景点的信息,最终决定从以下五个景点中选两个自驾游:这五个景点分别是晋中市的乔家大院和平遥古城,临汾市的壶口瀑布,运城市的七彩盐湖和鹳雀楼.分别用A,B,C,D,E五张卡片(除编号外其余完全相同)代表五个景点,并将五张卡片背面朝上洗匀放好,从中随机抽取两张,求抽到的两个景点恰好在同一个市的概率.
18如图,A,B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A﹣C﹣B行驶,全长68km.现开通隧道后,汽车直接沿直线AB行驶.已知∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据:≈1.4,≈1.7)
19如图,已知一次函数y1=k1x+b图象与x轴交于点C,与反比例函数的图象交于两点A(1,6),B(﹣3,﹣2),连接OA,OB.
(1)求一次函数及反比例函数的表达式;
(2)当y1>y2时,直接写出x的取值范围;
(3)若点P为x轴上一点,且△AOP的面积为△AOC面积的2倍,求点P的坐标.
20某专柜在销售某款红枣礼品的过程中发现:平均每天可售出20件,每件盈利40元,为了迎接“国庆中秋”双节,商场决定采取适当的降价措施(每件降价不超过15元),增加盈利.经市场调查发现:如果每件礼品降价1元,那么平均每天就可多售出2件.要想平均每天销售这种礼品盈利1200元,那么每件礼品应降价多少元?
21函数是刻画事物运动变化过程和发展规律的数学模型,应用非常广泛.用图象的方法研究函数,形象直观.在现实生活中,我们常用图象的方法研究函数,例如,气温随着时间的变化、股票随着时间变化等,就常用图象法把函数关系表示出来,然后利用图象进一步分析它们的变化情况.
小明根据相关数据和学习函数的经验,对成人喝250毫升低度白酒后,其血液中酒精含量(毫克/百毫升)随时间变化的规律进行了探究,发现血液中酒精含量y是时间x的函数,其中y表示血液中酒精含量(毫克/百毫升),x表示饮酒后的时间(小时)
下表记录了6小时以内11个时间点血液中酒精含量y(毫克/百毫升)随饮酒后的时间x(小时)(x>0)的变化情况:
饮酒后的时间
x(小时)
…
1
2
3
4
5
6
…
血液中酒精含量y(毫克/百毫升)
…
150
200
150
45
…
下面是小明的探究过程请补充完整
(1)如图,在平面直角坐标系xOy中,描出了上表中以各对对应值为坐标的点,根据描出的点,画出血液中酒精含量y随时间x变化的函数图象;
(2)观察函数图象,写出一条该函数的性质: .
(3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完250毫升低度白酒,第二天早上7:30能否驾车去上班?请说明理由.
22图1是一台实物投影仪,图2是它的示意图,折线B﹣A﹣O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.8cm,CD=8cm,AB=30cm,BC=35cm.(结果精确到0.1).
(1)如图2,∠ABC=70°,BC∥OE.
①填空:∠BAO= °.
②求投影探头的端点D到桌面OE的距离.
(2)如图3,将(1)中的BC向下旋转,当投影探头的端点D到桌面OE的距离为6cm时,求∠ABC的大小.
(参考数据:sin70°≈0.94,cos20°≈0.94,sin36.8°≈0.60,cos53.2°≈0.60)
23如图,三角形纸片ABC,分别取AB、AC的中点D、G,沿DG折叠,使点A的对应点A′落在BC边上;继续将纸片折叠,使BD与DA′重合,CG与GA′重合,折痕分别为DE,GF,折叠后的三个三角形拼合形成一个矩形.连接AA′,则AA′为△ABC的高线.
(1)若△ABC面积为10,则矩形DEFG的面积为 ;
(2)若点A′恰好是边BC的中点,求证:四边形ADA′G为菱形;
(3)当△ABC满足什么条件时,矩形DEFG为正方形,请说明理由.
参考答案与试题解析
一.选择题(共10小题)
1.在Rt△ABC中,∠C=90°,tanA=,则cosA等于( )
A. B. C. D.
【分析】根据tanA=求出第三边长的表达式,求出cosA即可.
【解答】解:如图:
设BC=5x,
∵tanA=,
∴AC=12x,AB==13x,
∴cosA===.
故选:D.
2.把二次函数y=﹣x2﹣2x+3配方化为y=a(x﹣h)2+k形式是( )
A.y=﹣(x﹣1)2﹣4 B.y=﹣(x+1)2+4
C.y=﹣(x﹣1)2+3 D.y=﹣(x+1)2﹣3
【分析】利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,即可把一般式转化为顶点式.
【解答】解:y=﹣x2﹣2x+3
=﹣(x2+2x+1)+3+1
=﹣(x+1)2+4,
即y=﹣(x+1)2+4.
故选:B.
3.对于反比例函数y=,下列判断正确的是( )
A.图象经过点(﹣1,3)
B.图象在第二、四象限
C.不论x为何值,y>0
D.图象所在的第一象限内,y随x的增大而减小
【分析】根据反比例函数y=的性质:当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小,以及凡是反比例函数经过的点横纵坐标之积=k进行分析即可.
【解答】解:A、图象经过点(﹣1,3),说法错误;
B、图象在第二、四象限,说法错误;
C、不论x为何值,y>0,说法错误;
D、图象所在的第一象限内,y随x的增大而减小,说法正确;
故选:D.
4.矩形具有但菱形不一定具有的性质是( )
A.对边平行且相等 B.对角相等、邻角互补
C.对角线相等 D.对角线互相垂直
【分析】根据矩形的性质和菱形的性质对选项进行逐一判断,选择出矩形具有而菱形不一定具有的性质即可.
【解答】解:A、对边平行且相等,是矩形的性质,也是菱形的性质,故A不符合题意.
B、对交相等,邻角互补,是矩形的性质,也是菱形的性质,故B不符合题意.
C、对角线相等,是矩形的性质,但不是菱形的性质,故C符合题意.
D、对角线互相垂直,是菱形的性质,但不是矩形的性质,故D不符合题意.
故选:C.
5.在平面直角坐标系中,将函数y=﹣2x2的图象先向右平移1个单位长度,再向上平移5个单位长度,得到图象的函数解析式是( )
A.y=﹣2(x+1)2+5 B.y=﹣2(x﹣1)2+5
C.y=﹣2(x+1)2﹣5 D.y=﹣2(x﹣1)2﹣5
【分析】直接根据“上加下减,左加右减”的原则进行解答即可.
【解答】解:由“左加右减”的原则可知,
抛物线y=﹣2x2的图象向右平移1个单位所得函数图象的关系式是:y=﹣2(x﹣1)2;
由“上加下减”的原则可知,
抛物线y=﹣2(x﹣1)2的图象向上平移5个单位长度所得函数图象的关系式是:y=﹣2(x﹣1)2+5.
故选:B.
6.如图,已知∠1=∠2,则添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )
A. B. C.∠B=∠ADE D.∠C=∠E
【分析】证出∠DAE=∠BAC,由相似三角形的判定方法即可得出结果.
【解答】解:∵∠1=∠2,
∴∠DAE=∠BAC,
A、添加,无法判定△ABC∽△ADE,故本选项正确;
B、添加,可用两边及其夹角法判定△ABC∽△ADE,故本选项错误;
C、添加∠B=∠ADE,可用两角法判定△ABC∽△ADE,故本选项错误;
D、添加∠C=∠E,可用两角法判定△ABC∽△ADE,故本选项错误;
故选:A.
7.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b和反比例函数y=在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
【分析】根据二次函数y=ax2+bx+c的图象开口向上,得出a>0,与y轴交点在y轴的正半轴,得出c>0,利用对称轴x=﹣>0,得出b<0,进而对照四个选项中的图象即可得出结论.
【解答】解:因为二次函数y=ax2+bx+c的图象开口向上,得出a>0,与y轴交点在y轴的正半轴,得出c>0,利用对称轴x=﹣>0,得出b<0,
所以一次函数y=ax+b经过一、三、四象限,反比例函数y=经过一、三象限,
故选:D.
8.如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=3m,则AB的长度为( )
A.6m B.3m C.9m D.6m
【分析】根据坡度的概念求出AC,根据勾股定理求出AB.
【解答】解:∵迎水坡AB的坡比为1:,
∴=,即=,
解得,AC=3,
由勾股定理得,AB==6(m),
故选:A.
9.下列图形中,阴影部分面积最大的是( )
A. B.
C. D.
【分析】分别根据反比例函数系数k的几何意义以及三角形面积求法以及梯形面积求法得出即可.
【解答】解:A、根据反比例函数系数k的几何意义,阴影部分面积和为:xy=3,
B、根据反比例函数系数k的几何意义,阴影部分面积和为:3,
C、根据反比例函数系数k的几何意义,以及梯形面积求法可得出:
阴影部分面积为:3+×(1+3)×2﹣﹣=4,
D、根据M,N点的坐标以及三角形面积求法得出,阴影部分面积为:×1×6=3,
阴影部分面积最大的是4.
故选:C.
10.探究课上,老师给出问题“一艘轮船上装有10吨货物,轮船到达目的地后开始卸货.设平均卸货速度为x吨/小时,卸完这批货物所需的时间为y小时.若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?”.如图,小华利用计算机先绘制出反比例函数的图象,并通过观察图象发现:当0<y≤5时,x≥2.所以小华得出此题答案为:平均每小时至少要卸货2吨.小华的上述方法体现的数学思想是( )
A.公理化 B.数形结合
C.分类讨论 D.由特殊到一般
【分析】根据题目中的信息即可得到体现的数学思想是数形结合.
【解答】解:小华的上述方法体现的数学思想是数形结合,
故选:B.
二.填空题(共5小题)
11.如图,在点A处测得点B处的仰角是 ∠4 .(用“∠1,∠2,∠3或∠4”表示)
【分析】根据仰角的定义即可得到结论.
【解答】解:在点A处测得点B处的仰角是∠4,
故答案为:∠4.
12.已知二次函数y=ax2+bx+c自变量x与函数值y之间满足右面表格中的数量关系:由表可知,该二次函数的对称轴是 直线x=3 .
x
2
4
5
y
0.2
0.2
2
【分析】根据表中数据得出(2,0.2)与(4,0.2)是关于对称轴对称的两个点,从而得出结论.
【解答】解:由表中数据知,x=2和x=4时对应函数值都是0.2,
∴(2,0.2)与(4,0.2)是关于对称轴对称的两个点,
∴对称轴直线为x==3,
故答案为:直线x=3.
13.如图,一次函数的图象分别交x轴,y轴于N,A两点,与反比例函数在第一象限的图象交于点B,若点N是线段AB的中点,则k的值为 4 .
【分析】先求出A,N坐标,再利用中点坐标公式求出点B坐标,再利用待定系数法求函数求k的值即可.
【解答】解:一次函数的图象分别交x轴,y轴于N,A两点,
令y1=0,则x﹣1=0,
解得:x=2,
∴点N坐标为(2,0),
令x=0,则y1=﹣1,
∴点A坐标为(0,﹣1),
又∵点N是线段AB的中点,设点B为(x,y),
∴2=,0=,
解得:x=4,y=1,
∴点B为(4,1),
∵点B在反比例函数的图象上,
∴1=,
∴k=4.
故答案为:4.
14.如图,在矩形ABCD中,,将矩形ABCD绕着点A逆时针旋转一定角度得到矩形AB′C′D′,若点B′落在边CD上,则∠DAD′= 30 °.
【分析】根据题意得AB'=AB=2AD,∠D=90°,则∠DB'A=30°,进而问题可解.
【解答】解:∵四边形ABCD是矩形,
∴∠D=∠DAB=90°,
∵,
∴AB=2AD,
∵将矩形ABCD绕着点A逆时针旋转一定角度得到矩形AB′C′D′,
∴∠D'AB'=∠DAB=90°,AB'=AB=2AD,
∴sin∠DB'A=,
∴∠DB'A=30°,
∴∠DAB'=60°,
∴∠DAD'=∠D'AB'﹣∠DAB'=30°,
故答案为30.
15.已知二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点B的坐标为(1,0),其图象如图所示,下列结论:①abc<0;②2a﹣b=0;③当y>0时,x>1;④3b+2c>0;⑤当x<0时,y随x的增大而减小;其中正确的有 ①② .(只填序号)
【分析】根据抛物线的开口方向、对称轴、顶点坐标、增减性逐个进行判断,得出答案.
【解答】解:∵抛物线的开口向上,
∴a>0,
∵对称轴是直线x=﹣1,
∴a、b同号,即b>0,
∵抛物线与y轴交在y轴的负半轴,
∴c<0,
∴abc<0,故①正确;
对称轴是直线x=﹣1,即﹣=﹣1,
∴2a﹣b=0,故②正确;
∵抛物线的对称轴为直线x=﹣1,与x轴的一个交点B的坐标为(1,0),
∴与x轴的另一个交点为(﹣3,0),
由图象可知y>0时,相应的x的取值范围为x<﹣3或x>1,故③错误;
由图象可知,x=1时,y=a+b+c<0,
∵2a﹣b=0,
∴a=b,
∴b+c<0,
∴3b+2c<0,故④错误;
∵在对称轴的左侧,y随x的增大而减小,
∴当x<﹣1时,y随x的增大而减小,故⑤错误;
综上所述,正确的结论有①②,
故答案为①②.
三.解答题
16.(1)解下列方程:x2﹣1=2(x+1);
(2)计算:+sin60°⋅cos45°﹣tan30°.
【分析】(1)利用因式分解法求解即可;
(2)将特殊角的三角函数值代入求解即可.
【解答】解:(1)(x+1)(x﹣1)﹣2(x+1)=0,
∴(x+1)(x﹣3)=0,
∴x+1=0或x﹣3=0,
∴x1=﹣1,x2=3.
(2)原式=
=
=.
17. 2020年国庆小长假,小华一家计划利用假期的时间出去旅游,他们收集了很多旅游景点的信息,最终决定从以下五个景点中选两个自驾游:这五个景点分别是晋中市的乔家大院和平遥古城,临汾市的壶口瀑布,运城市的七彩盐湖和鹳雀楼.分别用A,B,C,D,E五张卡片(除编号外其余完全相同)代表五个景点,并将五张卡片背面朝上洗匀放好,从中随机抽取两张,求抽到的两个景点恰好在同一个市的概率.
【考点】列表法与树状图法.版权所有
【专题】概率及其应用;推理能力.
【答案】.
【分析】列表可知共有20种等可能的结果,其中抽到两个景点在同一个市的结果有4种,再由概率公式求解即可.
【解答】解:列表如下:
第一张
第二张
A
B
C
D
E
A
(B,A)
(C,A)
(D,A)
(E,A)
B
(A,B)
(C,B)
(D,B)
(E,B)
C
(A,C)
(B,C)
(D,C)
(E,C)
D
(A,D)
(B,D)
(C,D)
(E,D)
E
(A,E)
(B,E)
(C,E)
(D,E)
由列表可知一共有20种等可能的结果,其中抽到两个景点在同一个市的结果有4种,
∴P(两个景点恰好在同一个市)=.
18如图,A,B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A﹣C﹣B行驶,全长68km.现开通隧道后,汽车直接沿直线AB行驶.已知∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据:≈1.4,≈1.7)
【考点】解直角三角形的应用.版权所有
【答案】见试题解答内容
【分析】首先过点C作CD⊥AB,垂足为D,设CD=x,即可表示出AC,BC的长,进而求出x的值,再利用锐角三角函数关系得出AD,BD的长,即可得出答案.
【解答】解:如图,过点C作CD⊥AB,垂足为D,设CD=x.
在Rt△ACD中,sin∠A=,AC==2x,
在Rt△BCD中,sin∠B=,BC==x,
∵AC+BC=2x+x=68
∴x=≈=20.
在Rt△ACD中,tan∠A=,AD==20,
在Rt△BCD中,tan∠B=,BD==20,
AB=20+20≈54,
AC+BC﹣AB=68﹣54=14.0(km).
答:隧道开通后,汽车从A地到B地比原来少走14.0千米.
19如图,已知一次函数y1=k1x+b图象与x轴交于点C,与反比例函数的图象交于两点A(1,6),B(﹣3,﹣2),连接OA,OB.
(1)求一次函数及反比例函数的表达式;
(2)当y1>y2时,直接写出x的取值范围;
(3)若点P为x轴上一点,且△AOP的面积为△AOC面积的2倍,求点P的坐标.
【考点】反比例函数与一次函数的交点问题.版权所有
【专题】反比例函数及其应用;应用意识.
【答案】(1)一次函数表达式为y1=2x+4;反比例函数表达式为;(2)﹣3<x<0或x>1;(3)点P的坐标为(4,0)或(﹣4,0).
【分析】(1)根据一次函数图象经过点A(1,6),B(﹣3,﹣2),用待定系数法求函数解析式即可;反比例函数图象经过点A(1,6),用待定系数法求函数解析式即可;
(2)根据函数图象可直接得到自变量x的取值范围;
(3)先根据已知条件求出S△AOC,再根据△AOP的面积为△AOC面积的2倍得出△AOP的面积,根据三角形面积公式求出OP=4,从而求出点P坐标.
【解答】解:(1)∵一次函数y1=k1x+b图象经过点A(1,6),B(﹣3,﹣2),
∴,
解得,
∴y1=2x+4;
又∵图象经过点A(1,6),
∴k2=1×6=6,
∴;
(2)由图象可得:当y1>y2时,则有﹣3<x<0或x>1;
(3)如图,过点A作AE⊥x轴于点E,则AE=6,
当y1=0时,2x+4=0,
解得x=﹣2
∴OC=2,
∴.
又∵△AOP面积为△AOC面积的2倍,
∴S△AOP=2S△AOC=2×6=12,
∴OP•AE=12,
∴OP=4,
∴点P的坐标为(4,0)或(﹣4,0).
20某专柜在销售某款红枣礼品的过程中发现:平均每天可售出20件,每件盈利40元,为了迎接“国庆中秋”双节,商场决定采取适当的降价措施(每件降价不超过15元),增加盈利.经市场调查发现:如果每件礼品降价1元,那么平均每天就可多售出2件.要想平均每天销售这种礼品盈利1200元,那么每件礼品应降价多少元?
【考点】一元二次方程的应用.版权所有
【专题】一元二次方程及应用;应用意识.
【答案】10元.
【分析】设每件礼品降价x元,则每件的利润为(40﹣x)元,平均每天可售出(20+2x)件,利用平均每天销售这种礼品获得的利润=每件的销售利润×平均每天的销售量,即可得出关于x的一元二次方程,解之即可得出x的值,再结合每件降价不超过15元,即可确定每件礼品应降低的价格.
【解答】解:设每件礼品降价x元,则每件的销售利润为(40﹣x)元,平均每天可售出(20+2x)件,
依题意得:(40﹣x)(20+2x)=1200,
整理得:x2﹣30x+200=0,
解得:x1=10,x2=20.
∵每件降价不超过15元,
∴x=10.
答:每件礼品盒应降价10元.
21函数是刻画事物运动变化过程和发展规律的数学模型,应用非常广泛.用图象的方法研究函数,形象直观.在现实生活中,我们常用图象的方法研究函数,例如,气温随着时间的变化、股票随着时间变化等,就常用图象法把函数关系表示出来,然后利用图象进一步分析它们的变化情况.
小明根据相关数据和学习函数的经验,对成人喝250毫升低度白酒后,其血液中酒精含量(毫克/百毫升)随时间变化的规律进行了探究,发现血液中酒精含量y是时间x的函数,其中y表示血液中酒精含量(毫克/百毫升),x表示饮酒后的时间(小时)
下表记录了6小时以内11个时间点血液中酒精含量y(毫克/百毫升)随饮酒后的时间x(小时)(x>0)的变化情况:
饮酒后的时间
x(小时)
…
1
2
3
4
5
6
…
血液中酒精含量y(毫克/百毫升)
…
150
200
150
45
…
下面是小明的探究过程请补充完整
(1)如图,在平面直角坐标系xOy中,描出了上表中以各对对应值为坐标的点,根据描出的点,画出血液中酒精含量y随时间x变化的函数图象;
(2)观察函数图象,写出一条该函数的性质: .
(3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完250毫升低度白酒,第二天早上7:30能否驾车去上班?请说明理由.
【考点】反比例函数的应用.版权所有
【专题】反比例函数及其应用;应用意识.
【答案】见试题解答内容
【分析】(1)利用描点法画出函数图象即可;
(2)根据图象写出一条性质即可;
(3)把y=20代入反比例函数得x=11.25.喝完酒经过11.25小时为早上7:20,即早上7:20以后血液中的酒精含量小于或等于20毫克/百毫升.由此即可判断;
【解答】解:(1)图象如图所示.
(2)当x<1时,y随x的增大而增大;
当x<时,图象关于直线x=1对称;
当x=1时,y有最大值,最大值为200;
故答案为:当x<1时,y随x的增大而增大(答案不唯一);
(3)由图象可知1.5时后(包括1.5时)y与x可近似地用反比例函数(k>0)刻画,
∵当x=5时,y=45,且(5,45)在反比例函数(k>0)图象上,
∴把(5,45)代入得,解得k=225,
把y=20代入反比例函数得x=11.25.
∴喝完酒经过11.25时(即11:15时)为早上7:15.
∴第二天早上7:30可以驾车去上班.
22图1是一台实物投影仪,图2是它的示意图,折线B﹣A﹣O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.8cm,CD=8cm,AB=30cm,BC=35cm.(结果精确到0.1).
(1)如图2,∠ABC=70°,BC∥OE.
①填空:∠BAO= °.
②求投影探头的端点D到桌面OE的距离.
(2)如图3,将(1)中的BC向下旋转,当投影探头的端点D到桌面OE的距离为6cm时,求∠ABC的大小.
(参考数据:sin70°≈0.94,cos20°≈0.94,sin36.8°≈0.60,cos53.2°≈0.60)
【考点】解直角三角形的应用.版权所有
【专题】解直角三角形及其应用.
【答案】见试题解答内容
【分析】(1)①过点A作AG∥BC,根据平行线的性质解答便可;
②过点A作AF⊥BC于点F,解直角三角形求出AF,进而计算AF+OA﹣CD使得结果;
(2)过点点D作DH⊥OE于点H,过点B作BM⊥CD,与DC延长线相交于点M,过A作AF⊥BM于点F,求出CM,再解直角三角形求得∠MBC便可.
【解答】解:(1)①过点A作AG∥BC,如图1,则∠BAG=∠ABC=70°,
∵BC∥OE,
∴AG∥OE,
∴∠GAO=∠AOE=90°,
∴∠BAO=90°+70°=160°,
故答案为:160;
②过点A作AF⊥BC于点F,如图2,
则AF=AB•sin∠ABF=30sin70°≈28.2(cm),
∴投影探头的端点D到桌面OE的距离为:AF+OA﹣CD=28.2+6.8﹣8=27.0(cm);
(2)过点DE⊥OE于点H,过点B作BM⊥CD,与DC延长线相交于点M,过A作AF⊥BM于点F,如图3,
则∠MBA=70°,AF=28.2cm,DH=6cm,BC=35cm,CD=8cm,
∴CM=AF+AO﹣DH﹣CD=28.2+6.8﹣6﹣8=21(cm),
∴sin∠MBC=,
∴∠MBC=36.8°,
∴∠ABC=∠ABM﹣∠MBC=33.2°.
23如图,三角形纸片ABC,分别取AB、AC的中点D、G,沿DG折叠,使点A的对应点A′落在BC边上;继续将纸片折叠,使BD与DA′重合,CG与GA′重合,折痕分别为DE,GF,折叠后的三个三角形拼合形成一个矩形.连接AA′,则AA′为△ABC的高线.
(1)若△ABC面积为10,则矩形DEFG的面积为 ;
(2)若点A′恰好是边BC的中点,求证:四边形ADA′G为菱形;
(3)当△ABC满足什么条件时,矩形DEFG为正方形,请说明理由.
【考点】三角形的面积;三角形中位线定理;菱形的判定与性质;矩形的判定与性质;正方形的判定;翻折变换(折叠问题).版权所有
【专题】等腰三角形与直角三角形;平移、旋转与对称;运算能力;推理能力.
【答案】(1)5;
(2)证明过程见解析;
(3)AA'=BC.
【分析】(1)由折叠的性质得出SΔDA'G=S△DAG,SΔDA'E=S△DBE,SΔGA'F=S△GFC,则可得出答案;
(2)由折叠可知A'D=AD,∠A'DG=∠ADG,A'G=AG,∠A'GD=∠AGD.得出AD=AG,根据菱形的判定可得出结论;
(3)由三角形中位线定理可得出DE=AA'.DG=BC,得出DE=DG,正方形的判定可得出结论.
【解答】解:(1)由题意知,SΔDA'G=S△DAG,SΔDA'E=S△DBE,SΔGA'F=S△GFC,
∴S矩形DEFG=SΔDA'G+SΔDA'E+SΔGA'F=S△ABC=5;
故答案为5.
(2)证明:由折叠可知A'D=AD,∠A'DG=∠ADG,A'G=AG,∠A'GD=∠AGD.
∵D,A'分别为AB,BC的中点,
∴DA'∥AC,DA'=AC,
∴∠A'DG=∠AGD,
∴∠ADG=∠AGD,
∴AD=AG,
∴A'D=AD=A'G=AG,
∴四边形ADA'G为菱形;
(3)AA'=BC.
理由如下:
∵D,E分别是AB,BA'的中点,
∴DE=AA'.
又∵D,G分别是AB,AC的中点,
∴DG=BC,
∵AA'=BC,
∴DG=DE.
∴矩形DEFG是正方形.
相关试卷
这是一份2021-2022学年度人教版九年级数学上册期中模拟试卷(含解析),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2021-2022学年度北师大版九年级数学上册期末模拟试卷(含解析),共23页。试卷主要包含了选择题,四象限D.第三,解答题等内容,欢迎下载使用。
这是一份2021-2022学年度人教版九年级数学上册第一次月考数学模拟试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。








