初中数学人教版八年级上册13.1.2 线段的垂直平分线的性质教学ppt课件

这是一份初中数学人教版八年级上册13.1.2 线段的垂直平分线的性质教学ppt课件，共18页。PPT课件主要包含了生活中的数学，活动一，自学提纲，三种语言，游戏中的数学，实战演练等内容，欢迎下载使用。
英山县政府为了方便居民的生活，计划在三个住宅小区A、B、C之间修建一个购物中心，试问，该购物中心应建于何处，才能使得它到三个小区的距离相等。
经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线
∵ AC=BC, CD ⊥AB, ∴ CD是AB的垂直平分线
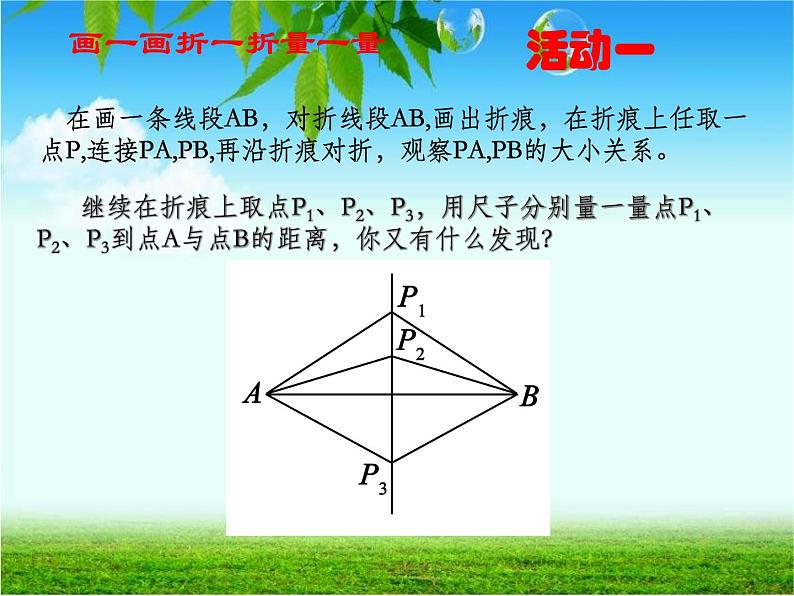
继续在折痕上取点P1、P2、P3，用尺子分别量一量点P1、P2、P3到点A与点B的距离，你又有什么发现？
在画一条线段AB，对折线段AB,画出折痕，在折痕上任取一点P,连接PA,PB,再沿折痕对折，观察PA,PB的大小关系。
在纸上画一条线段AB，对折线段，思考如下问题：（1）线段——（填“是”或“不是”)轴对称图形；（2）折痕与线段——（填“垂直”或“不垂直”；）（3）这条折痕是线段AB的————（4）在折痕上任找一点P，连接PA和PB,量一量PA与PB的长，PA与PB的关系是 ————（填“相等”或“不相等”） (5)通过测量，你发现P1A P1B； P2A P2BP3A P3B 由此你能得到什么结论？
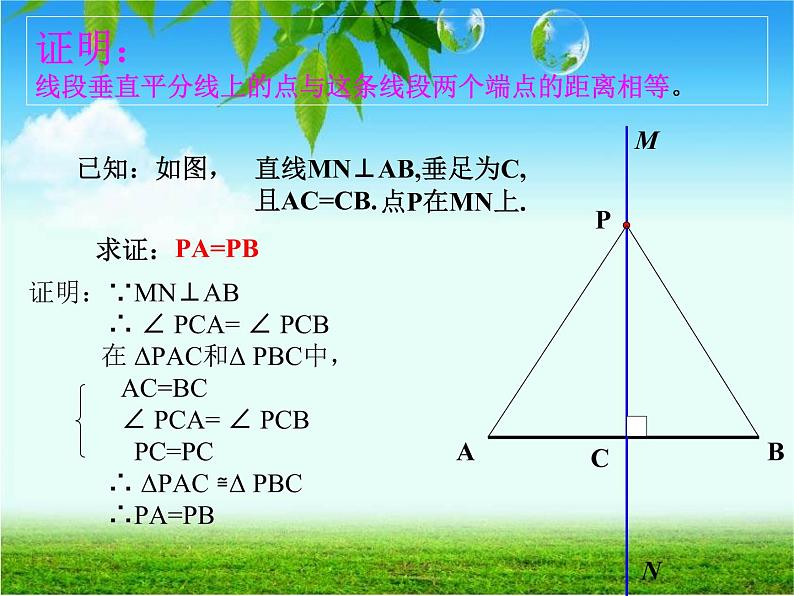
证明：线段垂直平分线上的点与这条线段两个端点的距离相等。
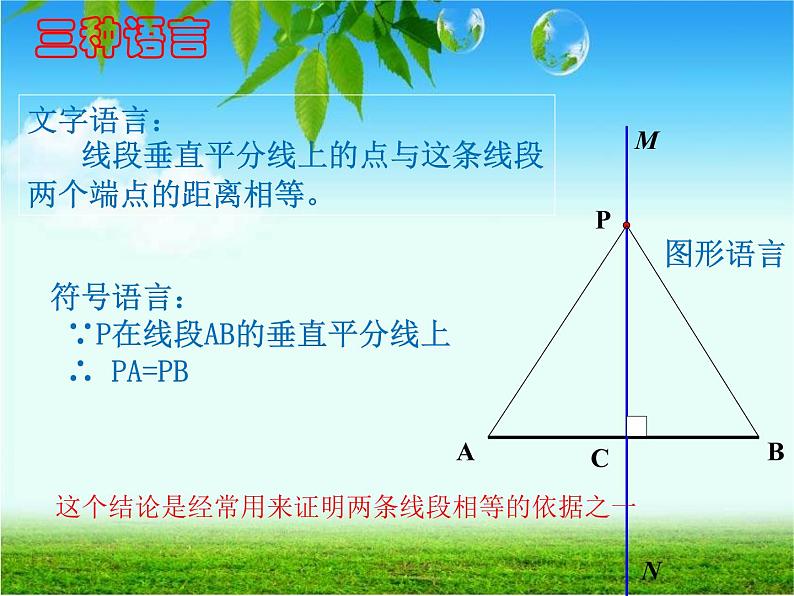
文字语言： 线段垂直平分线上的点与这条线段 两个端点的距离相等。
这个结论是经常用来证明两条线段相等的依据之一
符号语言： ∵P在线段AB的垂直平分线上 ∴ PA=PB
2、如图，在△ABC中，ED垂直平分AB，1) 若BD＝10，则AD=
2) 若AC＝14，△BCD的周长为24，则BC= 。
分线上的点到线段两端点的距离相等.
反过来: 如果PA=PB，P在线段AB的垂直平分线上吗?你能证明吗？
已知:如图,PA=PB.求证:点P在AB的垂直平分线上.
方法归纳：1，作垂直，证平分；2作平分，证垂直
文字语言： 到线段两个端点的距离相等的点在线段的垂直平分线上。
这个结论是经常用来证明点在直线上或直线过某一点的依据之一
符号语言： ∵PA=PB ∴ P在线段AB的垂直平分线上
思考：满足PA=PB的点P有多少个？这些点合在一起组成了什么图形？
本题主要考查：与一条线段两个端点距离相等的点，在这条线段的垂直平分线上；两点确定一条直线． 
A．AB垂直平分CD     B．CD垂直平分AB C．AB与CD互相垂直平分  D．CD平分∠ACB
如图，AC=AD，BC=BD，则有（　）．
反之：与一条线段两个端点距离相等的点，在这条线段的垂直平分线上。
性质：线段垂直平分线上的点与这条线段两个端点的距离相等。
英山县政府为了方便居民的生活，计划在三个住宅小区A、B、C之间修建一个购物中心，试问，该购物中心应建于何处，才能使得它到三个小区的距离相等。
数学问题源于生活实践，反过来数学又为生活实践服务
你能依据这一问题得到什么结论？
结论： 三角形三边垂直平分线交于一点，这一点到三角形三个顶点的距离相等。
实际问题