


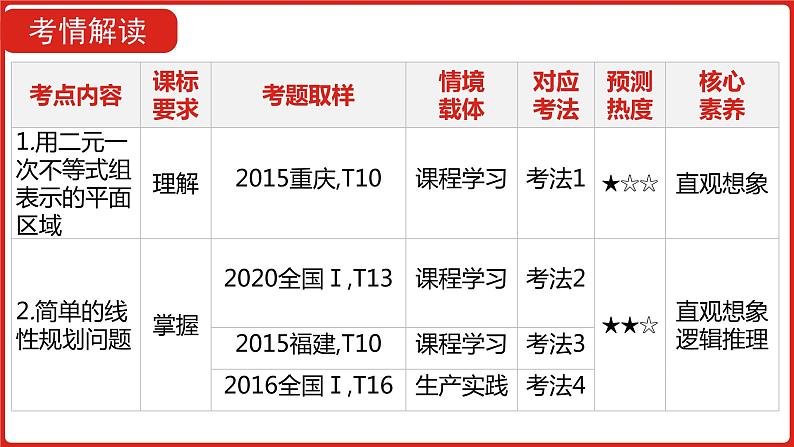




2022版高三全国统考数学(文)大一轮备考课件:第7章第2讲 二元一次不等式(组)与简单的线性规划问题
展开考点1 二元一次不等式(组)与平面区域
考点2 简单的线性规划问题
考法1 平面区域问题
考法2 求目标函数的最值(范围)
考法3 含参线性规划问题
考法4 线性规划的实际应用
考点1 二元一次不等式(组)与平面区域考点2 简单的线性规划问题
考点1 二元一次不等式(组)与平面区域
1.在平面直角坐标系中,平面内所有的点被直线Ax+By+C=0(A,B不同时为0)分成三类:①满足Ax+By+C=0的点;②满足Ax+By+C>0的点;③满足Ax+By+C<0的点.2.在平面直角坐标系中,Ax+By+C>0(或Ax+By+C<0)表示直线Ax+By+C=0某一侧的所有点组成的平面区域,且不含边界,作图时边界应画成虚线;在平面直角坐标系中,画Ax+By+C≥0(或Ax+By+C≤0)表示的平面区域时,边界应画成实线.3.由于将直线Ax+By+C=0同一侧的所有点(x,y)的坐标代入Ax+By+C所得到的实数的符号相同,所以只需在此直线的某一侧任取一特殊点(x0,y0),
由Ax0+By0+C的符号即可判断不等式Ax+By+C>0(或Ax+By+C<0)所表示的平面区域在直线的哪一侧.若直线不过原点(即C≠0),常把原点(0,0)作为特殊点.若直线经过原点(即C=0),常选(1,0),(-1,0),(0,1),(0,-1)等特殊点代入判断.4.画二元一次不等式(组)表示的平面区域的步骤可简记为:直线定界,虚实分明;特殊点定域,优选原点;阴影表示.注意不等式中有无等号,有等号时直线画成实线,无等号时直线画成虚线;不等式组表示的区域是各个不等式表示的区域的公共部分.
考点2 简单的线性规划问题
1.线性规划的有关概念
说明 如果目标函数存在一个最优解,那么最优解通常在可行域的顶点处取得;如果目标函数存在多个最优解,那么最优解一般在可行域的边界上取得.注意 最优解必定是可行解,但可行解不一定是最优解.最优解不一定唯一,有时有多个.
2.对线性目标函数z=Ax+By中的B的符号一定要注意,当B>0,直线z=Ax+By过可行域且在y轴上截距最大时,z值最大,在y轴上截距最小时,z值最小;当B<0,直线z=Ax+By过可行域且在y轴上截距最大时,z值最小,在y轴上截距最小时,z值最大.
考法1 平面区域问题考法2 求目标函数的最值(范围)考法3 含参线性规划问题考法4 线性规划的实际应用
考法1 平面区域问题
思维导引 先正确作出不含参数m的不等式构成的二元一次不等式组所表示的平面区域,然后通过平移直线x-y=0来观察原不等式组所围成平面区域的形状是否为三角形,从而得出参数m的取值范围,最后根据不等式组表示的平面区域的面积求出参数m的值.
感悟升华 求平面区域的面积对平面区域的形状进行分析,若为三角形,应确定底与高,若为规则四边形(如平行四边形或梯形),可利用面积公式直接求解,若为不规则四边形,可利用割补法求解.易错警示 在画二元一次不等式(组)表示的平面区域时,要注意以下两个问题:(1)边界线是虚线还是实线;(2)选取的平面区域在直线的哪一侧.
考法2 求目标函数的最值(范围)
命题角度1 求线性目标函数的最值
思维导引 思路一 先画出不等式组表示的平面区域,然后平移直线x+7y=0,再根据目标函数的几何意义确定出其最大值.思路二 先求出可行域各顶点的坐标,然后分别计算出各顶点处的目标函数值,再找出最大值.
方法技巧 求线性目标函数的最值的方法方法1 图解法(常用方法)用图解法求目标函数z=ax+by的最值的步骤:
注意 当b>0时,直线l0向上平移,z变大,向下平移,z变小;当b<0时,直线l0向上平移,z变小,向下平移,z变大.
方法2 界点定值法当目标函数和约束条件都是线性的,且对应目标函数的最优解是可行域所对应图形的边界或顶点,这时要求目标函数的最值只要把可行域的几个顶点代入,通过对比目标函数的对应取值,即可得到最优解.
命题角度2 求非线性目标函数的最值
思维导引 作出不等式组表示的平面区域,将目标函数化简变形,利用目标函数的几何意义,进而可得目标函数的取值范围.
解析 作出不等式组表示的平面区域如图7-2-4中阴影部分(不包括边界OB)所示,其中A(1,2),B(0,2).
考法3 含参线性规划问题
思维导引 作出不等式组表示的平面区域,利用z的几何意义,结合z的最大值是最小值的4倍建立方程,即可得出结果.
解析 作出不等式组表示的平面区域如图7-2-5中阴影部分(包括边界)所示. (把参数当成常数)
方法技巧 由目标函数的最值求参数的方法1.把参数当常数用,根据线性规划问题的求解方法求出最优解,代入目标函数求出最值,通过构造方程或不等式求出参数的值或取值范围.2.先分离含有参数的式子,由数形结合确定含参数的式子所满足的条件,确定最优解的位置,从而求出参数.参数可能在表示可行域的不等式中(影响可行域的形状),也可能在目标函数中(影响最优解的位置),求解时注意参数的影响,有时需要对参数进行分类讨论.
示例5 某共享汽车品牌在某市投放1 500辆宝马轿车,为人们的出行提供了一种新的交通方式.该市的市民小王喜欢自驾游,他在该市通过网络组织了一场“周日租车游”活动,招募了30名自驾游爱好者租车旅游,他们计划租用A,B两种型号的宝马轿车,已知A,B两种型号的宝马轿车每辆的载客量都是5人,每天的租金分别为600元/辆和1 000元/辆,要求租车总数不超过12辆且不少于6辆,并且A,B两种型号的宝马轿车至少各租用1辆,则租车所需的租金最少为 元.
思维导引 先确定变量,然后根据已知条件列出变量所满足的不等式组以及目标函数,进而根据目标函数的几何意义确定最优解,求得目标函数的最值,最后还原为实际问题即可.
2022高三数学(理科)(全国版)一轮复习课件:第7章第2讲 二元一次不等式(组)与简单的线性规划问题: 这是一份2022高三数学(理科)(全国版)一轮复习课件:第7章第2讲 二元一次不等式(组)与简单的线性规划问题,共28页。PPT课件主要包含了考点帮·必备知识通关,考法帮·解题能力提升,考情解读,图7-2-1,图7-2-2,图7-2-3,图7-2-4,图7-2-5,图7-2-6等内容,欢迎下载使用。
2022版高三全国统考数学(文)大一轮备考课件:第2章第7讲 函数与方程: 这是一份2022版高三全国统考数学(文)大一轮备考课件:第2章第7讲 函数与方程,共36页。PPT课件主要包含了提能力∙数学探索,考情解读,考点帮·必备知识通关,零点存在性定理,考法帮·解题能力提升,图2-7-1,答案B,图2-7-3,图2-7-4,答案C等内容,欢迎下载使用。
2022版高三全国统考数学(文)大一轮备考课件:第2章第6讲 函数的图象: 这是一份2022版高三全国统考数学(文)大一轮备考课件:第2章第6讲 函数的图象,共37页。PPT课件主要包含了考点函数的图象,通思想∙方法指导,考情解读,考点帮·必备知识通关,考法帮·解题能力提升,图2-6-1,图2-6-2,图2-6-4,图2-6-5,图2-6-6等内容,欢迎下载使用。












