初中数学北师大版九年级上册2 矩形的性质与判定图片课件ppt

这是一份初中数学北师大版九年级上册2 矩形的性质与判定图片课件ppt，共21页。PPT课件主要包含了学习目标，新课导入，中心对称图形，新课讲授，合作探究，猜想1，矩形的对称性，轴对称图形，典例精析，随堂练习等内容，欢迎下载使用。
1.理解矩形的概念，了解它与平行四边形之间的关系.2.能用综合法证明矩形的性质定理以及相关结论，进一步发展推理能力.
平行四边形的对边平行且相等；
平行四边形的对角线互相平分；
在同一平面内两组对边分别平行的四边形叫做平行四边形.
平行四边形的对角相等，邻角互补；
下面几幅图片中都含有一些平行四边形. 观察这些平行四边形，你能发现它们有什么样的共同特征？
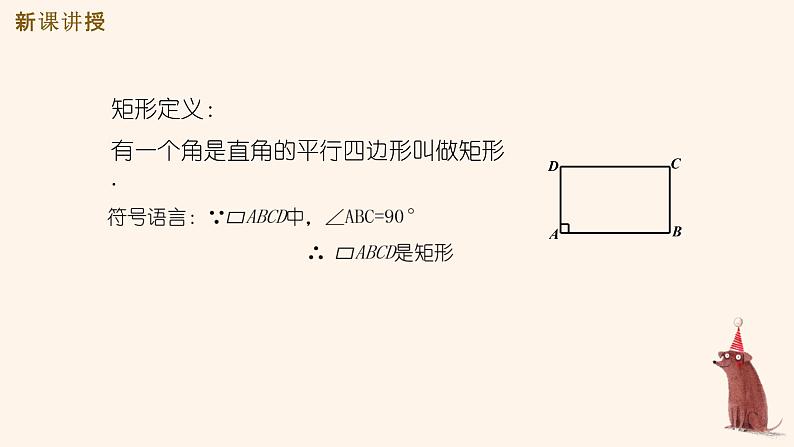
矩形定义：有一个角是直角的平行四边形叫做矩形.
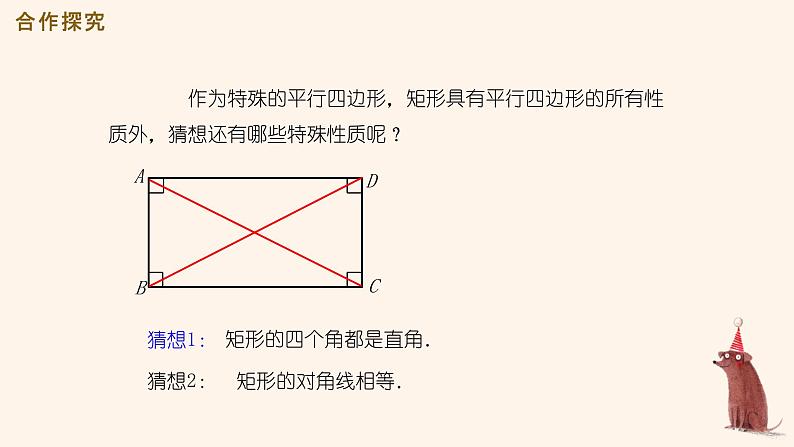
作为特殊的平行四边形，矩形具有平行四边形的所有性质外，猜想还有哪些特殊性质呢？
矩形的四个角都是直角．
已知：四边形ABCD是矩形， ∠B=900求证：∠A=∠C=∠D=90°
证明：∵矩形ABCD是平行四边形（已知） ∴ ∠B+∠C=180 °（平行四边形邻角互补） 又 ∵ ∠B=90° （已知） ∴ ∠C=90 °（等式的性质）同理：∠D=90° ，∠A=90° ∴∠A=∠B=∠C=∠D=90°
猜想2： 矩形的对角线相等．
已知：四边形ABCD是矩形，求证： AC = BD
证明： ∵ABCD是矩形（已知）
∴∠ABC = ∠DAB = 90° BC = AD（平行四边形的性质）
∴△ABC≌△BAD（SAS）
∴AC = BD（对应边相等）
在△ABC和△BAD中
AB = BA ∠ABC = ∠DAB = 90° BC = AD
定理：矩形的四个角都是直角
定理：矩形的对角线相等
矩形区别于平行四边形的性质
问题：（1）矩形的两条对角线可以把矩形分成几个直角三角形？ （2）BO是Rt△ABC中一条怎样的特殊线段？它与AC有什么大小关系？（3）你能借助于矩形加以证明吗？
矩形对角线相等且相互平分
  直角三角形斜边上的中线的性质
例1、如图，矩形ABCD中，对角线AC，BD相交于点O，∠BOC=120°，AB=6. 求：(1)对角线长 ；(2)BC的长 ；(3)矩形的面积.
解：　(1)∵四边形ABCD是矩形，∴AC=BD，OA=OC，OB=OD，∴OA=OB.∵∠BOC=120°，∴∠AOB=60°，∴△AOB是等边三角形，∴OA=AB=6，∴BD=AC=2OA=2×6=12.
例2、如图，BD，CE是△ABC的高，G，F分别是BC，DE的中点.求证：FG⊥DE.
例3、将矩形ABCD沿直线AE折叠，顶点D恰好落在BC边上的点F处，已知CE=3，AB=8，求图中阴影部分的面积.
1．下列说法错误的是(　　)A.矩形的对角线互相平分B.矩形的对角线相等C.有一个角是直角的四边形是矩形D.有一个角是直角的平行四边形叫作矩形
2．如图，在矩形ABCD中，AC，BD相交于点交O，AE平分∠BAD交BC于点E，若∠EAO＝15°，则∠BOE的度数为(　　)A.85° B.80° C.75° D.70°
5、如图，在矩形ABCD中，AE⊥BD于点E，对角线AC、BD相交于 点O，且BE∶ED=1∶3，AD=6 cm，求AE的长.