数学25.1 比例线段教学演示ppt课件

这是一份数学25.1 比例线段教学演示ppt课件，共22页。PPT课件主要包含了注意化单位哦，adbc，比例的基本性质，推理验证，比例的其它性质，1已知，用“设k法”，百炼成钢，黄金身材比例，黄金分割与生活等内容，欢迎下载使用。

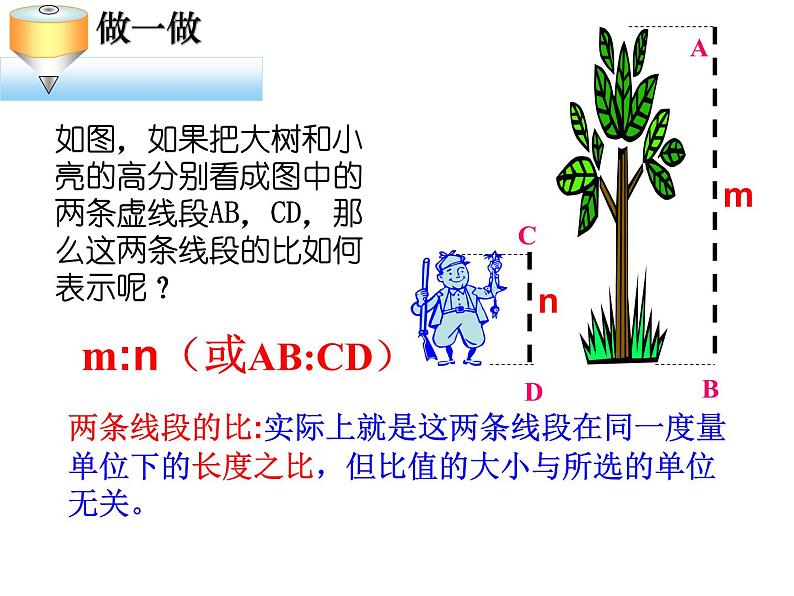
如图，如果把大树和小亮的高分别看成图中的两条虚线段AB，CD，那么这两条线段的比如何表示呢？
m:n（或AB:CD）
两条线段的比:实际上就是这两条线段在同一度量单位下的长度之比，但比值的大小与所选的单位无关。
（1）两条线段的比：如果选用同一个长度单位，量得两条线段AB，CD的长度分别是m,n,那么就说这两条线段的比AB:CD=m:n，或写成 。
注意：引入比值k的方法是解决比例问题的一种重要方法,以后经常会用到。
练习1：已知教室黑板的长 a = 3.2 m，宽 b = 120 cm ，求 a：b
解：a ：b = 320 ：120 = 8 ：3
练习2：在Rt△ABC中，∠C=90°， CD是AB边的中线，求CD ：AB
解：CD：AB = 1 ：2
练习3：在比例尺是1：6000000的地图上，量得南京到北京的距离是9厘米，南京到北 京的实际距离是 千米。
3.在RtΔABC中 ,AC=8,斜边BC=10,则ΔABC中的最短边与最长边的比值是__________
1.画在图纸上的某一零件的长是32mm,如果比例尺是1:20,则该零件的实际长度为 ( ) B. 640mm D.608mm
2.在比例尺为1:8000的某学校地图上,矩形运动场的图上尺寸是1cm×2cm,则矩形运动场的实际尺寸是_______________
4.等腰RtΔABC的斜边与直角边之比是_______
长160 m,宽80m
四条线段a、b、c、d中,如果 a与b的比等于c与d的比，即 a/b=c/d，那么这四条线段 a、b、c、d 叫做成比例线段,简称比例线段.
如果a,b,c,d 四个数满足a/b=c/d, 那么ad=bc 吗？反过来，如果ad=bc，那么a/b=c/d 吗？与同伴交流。
ad =bc
这实际上是：比例的合分比性.
这实际上是：比例的等比性.
那么b叫作a和d的比例中项。
如果点C把线段AB分成两条线段，使AB:AC=AC:BC,那么点C叫作线段AB的黄金分割点。AC是AB和BC的比例中项，AC与AB的比叫作黄金比。
想一想：一条线段上有几个黄金分割点？
探索身边的“黄金分割”
为什么翩翩起舞的芭蕾舞演员要掂起脚? 为什么身材苗条的时装模特还要穿高跟鞋?为什么她们会给人感到和谐、平衡、舒适、美的感觉?
黄金分割 与生活
由黄金分割画出的正五角星形,有庄严雄健之美.
古希腊时期的 巴台农神庙
如图是古希腊时期的巴台农神庙, 如果把图中虚线表示的矩形画成下图中的ABCD，以矩形ABCD的宽为边在其内部作正方形AEFD,那么我们可以惊奇的发现
点E是AB的黄金分割点吗?矩形ABCD的宽与长的比是黄金比吗?
请用所学知识回答上面的问题
打开地图，你就会发现那些好茶产地大多位于北纬30度左右。特别是红茶中的极品“祁红”，产地在安徽的祁门，也恰好在此纬度上。这不免让人联想起许多与北纬30度有关的地方。奇石异峰，名川秀水的黄山，庐山，九寨沟等等。衔远山，吞长江的中国三大淡水湖也恰好在这黄金分割的纬度上。
蝴蝶身长与双翅展开后的长度之比, 普通树叶的宽与长之比也接近0.618; 节目主持人报幕，绝对不会站在舞台的中央，而总是站在舞台的1／3处，站在舞台上侧近于0.618的位置才是最佳的位置; 生活中用的纸为黄金矩形，这样的长方形让人看起来舒服顺眼，正规裁法得到的纸张，不管其大小，如对于8开、16开、32开等，都仍然是近似的黄金矩形。
文明古国埃及的金字塔，形似方锥，大小各异。但这些金字塔底面的边长与高这比都接近于0.618.
古希腊的一些神庙，在建筑时高和宽也是按黄金比0.618来建立，他们认为这样的长方形看来是较美观；其大理石柱廓，就是根据黄金分割律分割整个神庙的.