冀教版九年级上册28.4 垂径定理图文ppt课件

这是一份冀教版九年级上册28.4 垂径定理图文ppt课件，共16页。PPT课件主要包含了探究一垂径定理，几何语言，∴AEBE，设☉O的半径为r，在Rt△OAE中，或14等内容，欢迎下载使用。

如图，在河北赵县境内，有一座建于隋代的石拱桥---赵州桥,它的桥拱是圆弧形,跨度(弧所对的弦的长)为37.4 m,拱高(弧的中点到弦的距离)为7.2 m,你能求出桥拱的半径吗?(结果保留小数点后一位)
任意作一条弦AB；过圆心O作弦AB的垂线,得直径CD交AB于点E.
问题1：沿着CD所在的直线将圆折叠,哪些线段 重合？哪些弧重合？你得出什么结论?
问题2：图形中的已知是什么?根据你得出的结论，能说出你的证明过程吗?
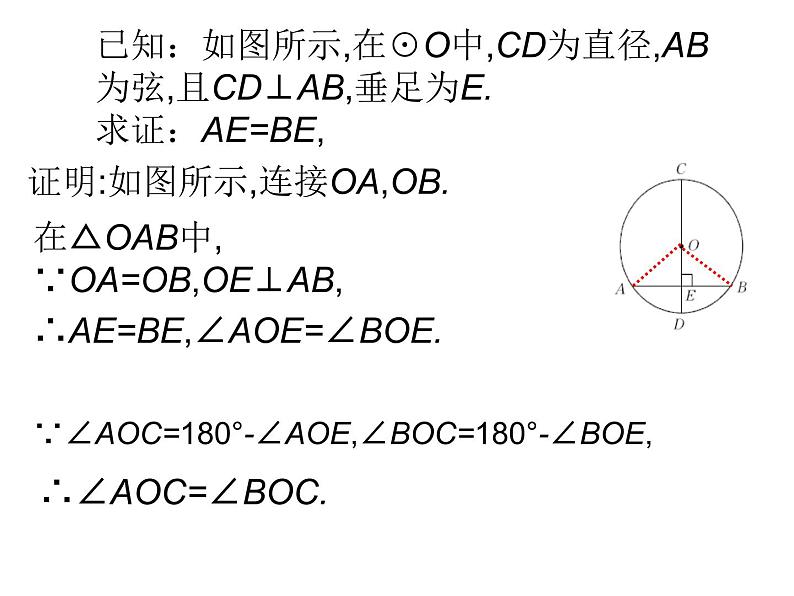
已知：如图所示,在☉O中,CD为直径,AB为弦,且CD⊥AB,垂足为E.求证：AE=BE,
证明:如图所示,连接OA,OB.
在△OAB中,∵OA=OB,OE⊥AB,
∴AE=BE,∠AOE=∠BOE.
∵∠AOC=180°-∠AOE,∠BOC=180°-∠BOE,
∴∠AOC=∠BOC.
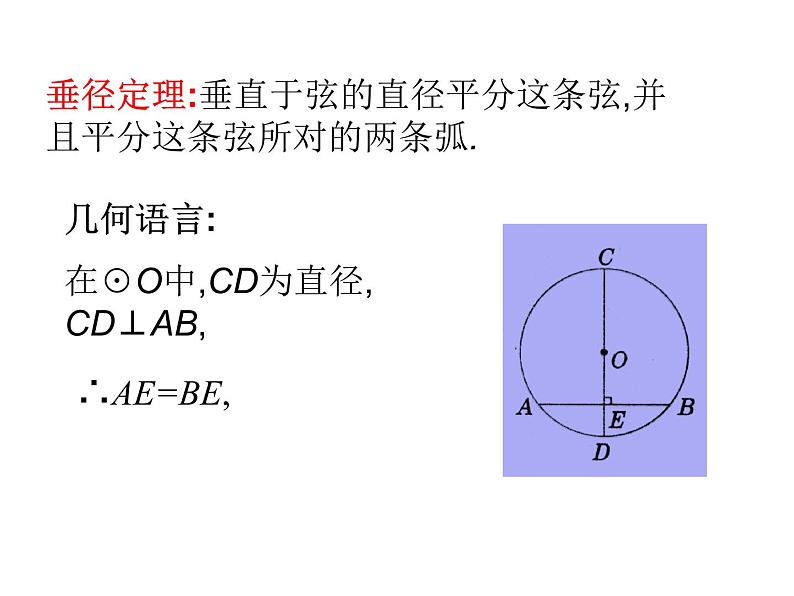
垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
在☉O中,CD为直径,CD⊥AB,
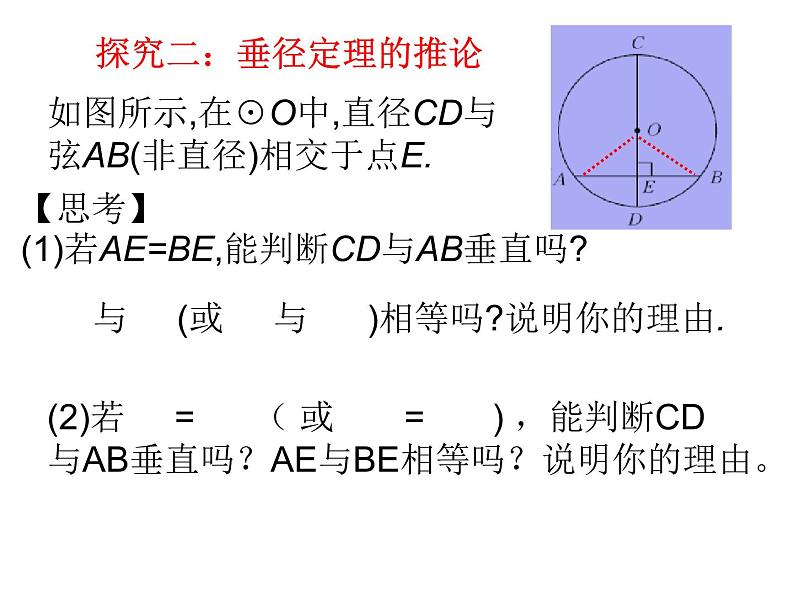
探究二：垂径定理的推论
如图所示,在☉O中,直径CD与弦AB(非直径)相交于点E.
【思考】(1)若AE=BE,能判断CD与AB垂直吗?
与 (或 与 )相等吗?说明你的理由.
(2)若 = （ 或 = ) ，能判断CD与AB垂直吗？AE与BE相等吗？说明你的理由。
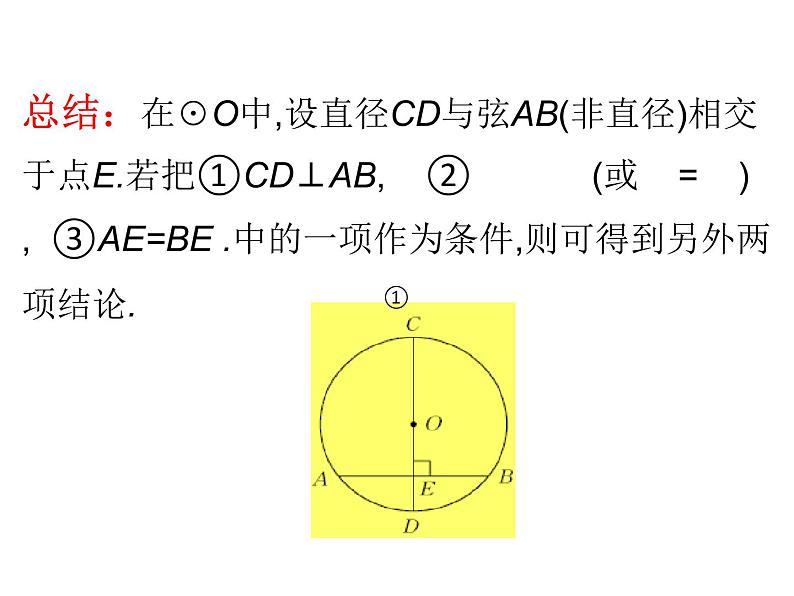
总结：在☉O中,设直径CD与弦AB(非直径)相交于点E.若把①CD⊥AB, ② (或 = ), ③AE=BE .中的一项作为条件,则可得到另外两项结论.
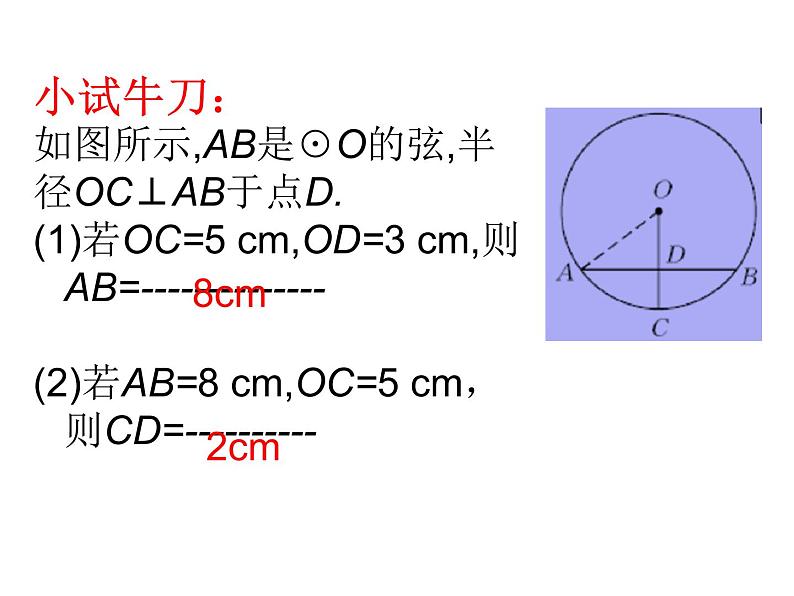
小试牛刀：如图所示,AB是☉O的弦,半径OC⊥AB于点D.(1)若OC=5 cm,OD=3 cm,则AB=--------------(2)若AB=8 cm,OC=5 cm，则CD=----------
例题：如图所示,已知CD为☉O的直径,AB为弦,且AB⊥CD,垂足为E.若ED=2,AB=8,求直径CD的长.
解:如图所示,连接OA.
∵CD为☉O的直径,AB⊥CD,∴AE=BE.
∵AB=8,∴AE=BE=4.
OA2=OE2+AE2,OE=OD-ED,
即r2=(r-2)2+42.解得r=5,从而2r=10.
所以直径CD的长为10.
如图，在河北赵县境内，有一座建于隋代的石拱桥---赵州桥,它的桥拱是圆弧形,跨度(弧所对的弦的长)为37.4 m,拱高(弧的中点到弦的距离)为7.2 m,你能求出桥拱的半径吗?(结果保留小数点后一位)
解:如图所示,用 表示主桥拱,设 所在圆的圆心为O,半径为R.
过圆心O作OC⊥AB于点D，交 于点C,连接OA.根据垂径定理知D为AB的中点,C为 的中点,CD就是拱高.
由题设可知,AB=37.4 m,CD=7.2 m,
所以AD= AB= ×37.4=18.7(m),
OD=OC-CD=R-7.2(m).
在Rt△OAD中,由勾股定理,得OA2=AD2+OD2,
即R2=18.72+(R-7.2)2.解得R≈27.9(m).因此,赵州桥的主桥拱半径约为27.9 m.
1.如图所示,AB是☉O的直径,CD是弦,CD⊥AB于点E,则下列结论不一定成立的是(　　)A.∠COE=∠DOE B.CE=DEC.OE=BE D.
2.某公园中央地上有一个大理石球，小明想测量球的半径，于是找了两块厚20cm的砖塞在球的两侧（如图所示），他量了下两砖之间的距离刚好是80cm，聪明的你请算出大石头的半径（ ）A.40cm B.30cm C.20cm D.50cm
3.如图，⊙O的直径CD过弦EF的中点G，∠DCF=20°，则∠EOD等于（　　）A．10° B．20° C．40° D．80°
4在半径为10的圆O中，弦AB∥CD，AB=12，CD=16，则这两条平行弦AB和CD间的距离为（ ）
2.（2017广安）如图，AB是⊙O的直径，且经过弦CD的中点H，已知cs∠CDB=4：5，BD=5，则OH的长度为（　）A. 2:5 B. 5:6 C. 1 D. 7:6
1.如图所示,☉O的直径为10,弦AB=8,P是弦AB上一动点,则线段OP的长的取值范围是（ ）A.OP≤5 B.OP≥3 C.3＜OP＜5 D.3≤OP≤5
3.如图，已知⊙O，线段AB与⊙O交于C、D两点且OA=OB，求证：AC=BD．