江苏省沭阳县修远中学2020-2021学年八年级上学期9月月考数学【试卷+答案】

这是一份江苏省沭阳县修远中学2020-2021学年八年级上学期9月月考数学【试卷+答案】，共25页。试卷主要包含了选择题，填空题，简答题等内容，欢迎下载使用。
一、选择题（本大题共8小题，每小题3分，共24分）
1. 下列图形中，不是轴对称图形的是（ ）
A. B. C. D.
2. 如图，在下列条件中，不能证明△ABD≌△ACD的是（ ）.
A. BD=DC，AB=ACB. ∠ADB=∠ADC，BD=DC
C. ∠B=∠C，∠BAD=∠CADD. ∠B=∠C，BD=DC
3. 已知△ABC≌△DEF，∠A=50°，∠B=75°，则∠F的大小为（ ）
A. 50°B. 55°C. 65°D. 75°
4. 一个等腰三角形周长为16，其中一边长为4，则这个等腰三角形的底边长是（ ）
A. 4B. 6C. 8D. 4或8
5. 如图是5×5的正方形网络，以点D，E为两个顶点作位置不同的格点三角形，使所作的格点三角形与△ABC全等，这样的格点三角形最多可以画出（ ）
A. 2个B. 4个C. 6个D. 8个
6. 如图，在△ABC中，AB=AC，AD平分∠BAC，DE⊥AB，DF⊥AC，E、F为垂足，则下列四个结论：（1）∠DEF=∠DFE；（2）AE=AF；（3）AD平分∠EDF；（4）EF垂直平分AD．其中正确有（ ）
A. 1个B. 2个C. 3个D. 4个
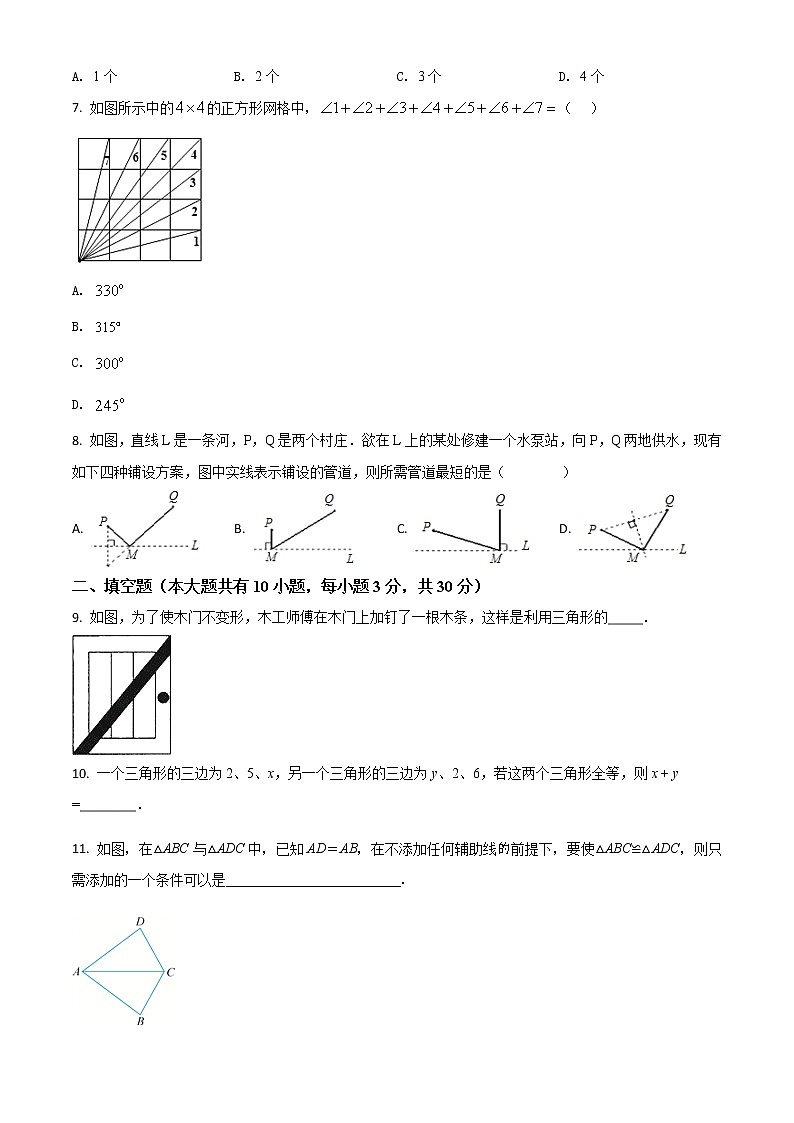
7. 如图所示中的的正方形网格中，（ ）
A.
B.
C.
D.
8. 如图，直线L是一条河，P，Q是两个村庄．欲在L上的某处修建一个水泵站，向P，Q两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是（ ）
A. B. C. D.
二、填空题（本大题共有10小题，每小题3分，共30分）
9. 如图，为了使木门不变形，木工师傅在木门上加钉了一根木条，这样是利用三角形的_____．
10. 一个三角形的三边为2、5、x，另一个三角形的三边为y、2、6，若这两个三角形全等，则x + y =________．
11. 如图，在△ABC与△ADC中，已知AD＝AB，在不添加任何辅助线前提下，要使△ABC≌△ADC，则只需添加的一个条件可以是_________________________．
12. 如图，△ABD≌△CBD，若∠A=80°，∠ABC=70°，则∠ADC的度数为______．
13. 如图，把长方形ABCD沿EF对折，若∠1=500，则∠AEF的度数等于__.
14. 在△ABC中，∠A＝80°，当∠B＝_____时，△ABC是等腰三角形．
15. 如图，在等边三角形ABC中，BD=CE,AD,BE交于点F,则_________;
16. 如图，∠BAC=100°，若MP和NQ分别垂直平分AB和AC，则∠PAQ=________．

17. 已知一个三角形的两边长分别为5和3，则第三边上的中线x的取值范围是________．
18. △ABC中，AB=AC=12厘米，∠B=∠C，BC=8厘米，点D为AB的中点．如果点P在线段BC上以2厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．若点Q的运动速度为v厘米/秒，则当△BPD与△CQP全等时，v的值为___________．

三、简答题(共96分)
19. 请你先在BC上找一点P，使点P到AB、AC的距离相等，再在射线AP上找一点Q，使QB=QC．
20. 如图，AB=CB，BE=BF，∠1=∠2，证明：△ABE≌△CBF．
21. 如图，△ABC和△CED中，AB∥CD，AB=CE，∠B=∠E，求证：AC=CD
22. 如图，如果AB=AC，那么∠B=∠C吗？请说明理由．

23. 已知：如图，△ABC的两内角∠ABC、∠ACB的角平分线相交于点P．求证：点P在∠A的角平分线上．
24. 如图，在△ABC中，M、N分别是BC与EF的中点，CF⊥AB，BE⊥AC．求证：MN⊥EF．
25. 如图，点C是线段AB上除点A、B外的任意一点，分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE，连接AE交DC于M，连接BD交CE于N，连接MN．
（1）求证：AE＝BD；
（2）请判断△CMN形状，并说明理由．
26. 如图①，△ABC中，AB=AC，∠ABC、∠ACB的平分线交于O点，过O点作EF∥BC交AB、AC于E、F．
（1）猜想：EF与BE、CF之间有怎样的关系，并说明理由．
（2）如图②，若AB≠AC，其他条件不变，在第（1）问中EF与BE、CF间的关系还存在吗？若存在，请说明理由．
（3）如图③，若△ABC中∠ABC的平分线BO与三角形外角平分线CO交于O，过O点作OE∥BC交AB于E，交AC于F．这时EF与BE、CF关系又如何？请说明理由．
27. 经过顶点的一条直线，．分别是直线上两点，且．
（1）若直线经过的内部，且在射线上，请解决下面两个问题：
①如图1，若，，
则 ； （填“”，“”或“”）；
②如图2，若，请添加一个关于与关系的条件 ，使①中的两个结论仍然成立，并证明两个结论成立．
（2）如图3，若直线经过的外部，，请提出三条线段数量关系的合理猜想（不要求证明）．
江苏省沭阳县修远中学2020-2021学年八年级9月月考数学试题
一、选择题（本大题共8小题，每小题3分，共24分）
1. 下列图形中，不是轴对称图形的是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】
根据轴对称图形的概念，把一个图形沿着某条直线折叠，两边能够重合的图形是轴对称图形．
【详解】解：根据轴对称的概念：把一个图形沿着某条直线折叠，两边能够重合的图形是轴对称图形．
A．是轴对称图形；故此选项不符合题意；
B．不是轴对称图形；故此选项符合题意；
C．是轴对称图形；故此选项不符合题意；
D．是轴对称图形；故此选项不符合题意；
故选：B．
【点睛】此题主要考查了轴对称图形的定义，注意轴对称和轴对称图形的区别：轴对称指的是两个图形；轴对称图形指的是一个图形．
2. 如图，在下列条件中，不能证明△ABD≌△ACD的是（ ）.
A. BD=DC，AB=ACB. ∠ADB=∠ADC，BD=DC
C. ∠B=∠C，∠BAD=∠CADD. ∠B=∠C，BD=DC
【答案】D
【解析】
【分析】
两个三角形有公共边AD，可利用SSS，SAS，ASA，AAS的方法判断全等三角形．
解答：
【详解】分析：
∵AD=AD，
A、当BD=DC，AB=AC时，利用SSS证明△ABD≌△ACD，正确；
B、当∠ADB=∠ADC，BD=DC时，利用SAS证明△ABD≌△ACD，正确；
C、当∠B=∠C，∠BAD=∠CAD时，利用AAS证明△ABD≌△ACD，正确；
D、当∠B=∠C，BD=DC时，符合SSA的位置关系，不能证明△ABD≌△ACD，错误．
故选D．
【点睛】本题考查全等三角形的判定，熟练掌握判定定理是关键.
3. 已知△ABC≌△DEF，∠A=50°，∠B=75°，则∠F的大小为（ ）
A. 50°B. 55°C. 65°D. 75°
【答案】B
【解析】
由∠A=50°，∠B=75°，根据三角形的内角和定理求出∠C的度数，根据已知△ABC≌△DEF，利用全等三角形的性质得到∠F=∠C，即可得到答案．
解：∵∠A=50°，∠B=75°， 又∵∠A+∠B+C=180°，∴∠C=55°，∵△ABC≌△DEF，∴∠F=∠C，即：∠F=55°．
故选B．
4. 一个等腰三角形的周长为16，其中一边长为4，则这个等腰三角形的底边长是（ ）
A. 4B. 6C. 8D. 4或8
【答案】A
【解析】
【分析】
分4为等腰三角形的底边长与腰长两种情况进行讨论．
【详解】当4为等腰三角形的底边长时，腰长= ，则这个等腰三角形的其余两边长分别为6，6；
当4为等腰三角形的腰长时，底边长=16-4-4=8，4、4、8不能构成三角形．
故选:A．
【点睛】本题考查的是等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．
5. 如图是5×5的正方形网络，以点D，E为两个顶点作位置不同的格点三角形，使所作的格点三角形与△ABC全等，这样的格点三角形最多可以画出（ ）
A. 2个B. 4个C. 6个D. 8个
【答案】B
【解析】
试题分析：观察图形可知：DE与AC是对应边，B点的对应点在DE上方两个，在DE下方两个共有4个满足要求的点，也就有四个全等三角形．
根据题意，运用SSS可得与△ABC全等的三角形有4个，线段DE的上方有两个点，下方也有两个点．
故选B．
考点：本题考查三角形全等的判定方法
点评：解答本题的关键是按照顺序分析，要做到不重不漏．
6. 如图，在△ABC中，AB=AC，AD平分∠BAC，DE⊥AB，DF⊥AC，E、F为垂足，则下列四个结论：（1）∠DEF=∠DFE；（2）AE=AF；（3）AD平分∠EDF；（4）EF垂直平分AD．其中正确的有（ ）
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
试题分析：∵AB=AC，AD平分∠BAC，DE⊥AB，DF⊥AC
∴△ABC是等腰三角形，AD⊥BC，BD=CD，∠BED=∠DFC=90°
∴DE=DF
∴AD垂直平分EF
∴（4）错误；
又∵AD所在直线是△ABC的对称轴，
∴（1）∠DEF=∠DFE；（2）AE=AF；（3）AD平分∠EDF．
故选C．
考点：1.等腰三角形的判定与性质；2.线段垂直平分线的性质．
7. 如图所示中的的正方形网格中，（ ）
A.
B.
C.
D.
【答案】B
【解析】
【分析】
根据正方形的轴对称得，，，.
【详解】由图可知，所在的三角形与所在的三角形全等，
∴.
同理得，，.
又，
所以.
故选B.
【点睛】本题考查了全等三角形的性质，全等三角形的对应角相等.发现并利用全等三角形是解题的关键.
8. 如图，直线L是一条河，P，Q是两个村庄．欲在L上的某处修建一个水泵站，向P，Q两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是（ ）
A. B. C. D.
【答案】A
【解析】
【分析】
利用对称的性质，通过等线段代换，将所求路线长转化为两定点之间的距离．
【详解】作点P关于直线L的对称点P′，连接QP′交直线L于M．
根据两点之间，线段最短，可知选项D铺设的管道，则所需管道最短．
故选：A．
【点睛】本题考查了最短路径的数学问题．这类问题的解答依据是“两点之间，线段最短”．由于所给的条件的不同，解决方法和策略上又有所差别．
二、填空题（本大题共有10小题，每小题3分，共30分）
9. 如图，为了使木门不变形，木工师傅在木门上加钉了一根木条，这样是利用三角形的_____．
【答案】稳定性
【解析】
【分析】
三角形具有稳定性，其它多边形不具有稳定性，把多边形分割成三角形则多边形的形状就不会改变．
【详解】解：这样做的道理是利用三角形的稳定性．
故答案为：稳定性．
【点睛】本题考查三角形稳定性的实际应用，三角形的稳定性在实际生活中有着广泛的应用，如钢架桥、房屋架梁等，因此要使一些图形具有稳定的结构，往往通过连接辅助线转化为三角形而获得．
10. 一个三角形的三边为2、5、x，另一个三角形的三边为y、2、6，若这两个三角形全等，则x + y =________．
【答案】11
【解析】
【分析】
根据全等三角形的性质求出x和y即可.
【详解】解：∵这两个三角形全等
∴x=6，y=5
∴x + y =11
故答案为11.
【点睛】此题考查是全等三角形的性质，掌握全等三角形的对应边相等是解决此题的关键.
11. 如图，在△ABC与△ADC中，已知AD＝AB，在不添加任何辅助线的前提下，要使△ABC≌△ADC，则只需添加的一个条件可以是_________________________．
【答案】DC＝BC或∠DAC＝∠BAC(答案不唯一)
【解析】
【分析】
【详解】添加DC=BC，可根据全等三角形的判定SSS即可判定△ABC≌△ADC；添加，可根据全等三角形的判定SAS即可判定△ABC≌△ADC．
考点：全等三角形的判定.
12. 如图，△ABD≌△CBD，若∠A=80°，∠ABC=70°，则∠ADC的度数为______．
【答案】130°
【解析】
试题分析：∵△ABD≌△CBD，
∴∠C=∠A=80°，
∴∠ADC=360°﹣∠A﹣∠ABC﹣∠C=360°﹣80°﹣70°﹣80°=130°．
故答案为130°．
考点：全等三角形性质
13. 如图，把长方形ABCD沿EF对折，若∠1=500，则∠AEF的度数等于__.
【答案】
【解析】
【分析】
【详解】∵把矩形ABCD沿EF对折，∴AD∥BC，∠BFE=∠2，
∵∠1=50°，∠1+∠2+∠BFE=180°，∴∠BFE==65°，
∵∠AEF+∠BFE=180°，∴∠AEF=115°．
故答案为115°.
14. 在△ABC中，∠A＝80°，当∠B＝_____时，△ABC是等腰三角形．
【答案】20°或50°或80°．
【解析】
【分析】
分三种情况分析，可能是顶角，也有可能是底角.
【详解】∵∠A=80°，
∴①当∠B=80°时，△ABC是等腰三角形；
②当∠B=（180°﹣80°）÷2=50°时，△ABC是等腰三角形；
③当∠B=180°﹣80°×2=20°时，△ABC是等腰三角形；
故答案为80°或50°或20°
15. 如图，在等边三角形ABC中，BD=CE,AD,BE交于点F,则_________;
【答案】60°
【解析】
【分析】
根据等边三角形的性质可得AB=BC，∠ABC=∠C=60°，然后利用“边角边”证明△ABD和△BCE全等，根据全等三角形对应角相等可得∠BAD=∠CBE，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AFE=∠ABC，从而得解．
【详解】解：在等边△ABC中，AB=BC，∠ABC=∠C=60°，
在△ABD和△BCE中，
∵，
∴△ABD≌△BCE（SAS），
∴∠BAD=∠CBE，
在△ABF中，∠AFE=∠BAD+∠ABF=∠CBE+∠ABF=∠ABC=60°，
即∠AFE=60°．
故答案为：60°．
【点睛】本题考查了等边三角形的性质，全等三角形的判定与性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，证明△ABD和△BCE全等是解本题的难点，也是关键．
16. 如图，∠BAC=100°，若MP和NQ分别垂直平分AB和AC，则∠PAQ=________．

【答案】20°
【解析】
【分析】
由MP和NQ分别垂直平分AB和AC，可得PA=PB，AQ=CQ，即可证得∠B=∠BAP，∠C=∠CAQ，又由∠BAC=120°，可求得∠B+∠C的度数，即可得∠BAP+∠CAQ的度数，继而求得答案．
【详解】∵PM垂直平分AB，
∴PA=PB，
∴∠B=∠BAP，
同理：QC=QA，
∴∠C=∠CAQ，
∵∠BAC=100°，
∴∠B+∠C=80°，
∴∠BAP+∠CAQ=80°，
∴∠PAQ=∠BAC-∠BAP-∠CAQ=20°．
故答案为20°．
【点睛】此题考查了线段垂直平分线的性质以及等腰三角形的性质．注意求得∠BAP+∠CAQ的度数是关键．
17. 已知一个三角形的两边长分别为5和3，则第三边上的中线x的取值范围是________．
【答案】1＜x＜4
【解析】
如图所示，AB=3，AC=5，AD=x，
延长AD至E，使AD=DE，连接BE，CE，
在△BDE与△CDA中，，
∴△BDE≌△CDA，
∴AE=2x，BE=AC=5，
△ABE中，BE−AB