初中数学苏科版八年级上册3.1 勾股定理教案配套课件ppt

这是一份初中数学苏科版八年级上册3.1 勾股定理教案配套课件ppt，共25页。PPT课件主要包含了从身边小事做起，勾股定理一，学习目标，邮票赏析，探究活动1，探究活动2，用“补”的方法，用“割”的方法，实验操作1，实验操作2等内容，欢迎下载使用。
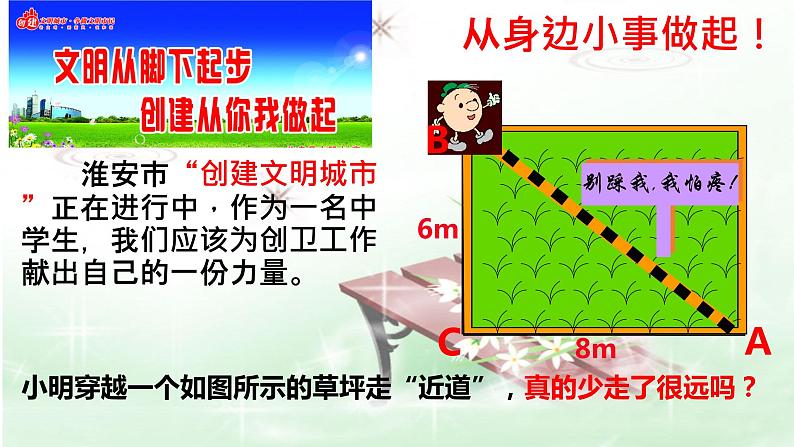
小明穿越一个如图所示的草坪走“近道”，真的少走了很远吗？
淮安市“创建文明城市”正在进行中，作为一名中学生，我们应该为创卫工作献出自己的一份力量。
数学中一颗璀璨的明珠，在人类的文明史上有着杰出的贡献。
1、体验勾股定理的探索过程，培养观察、猜想、分析和概括的能力。2、掌握勾股定理的内容，并运用勾股定理解决简单的实际问题。
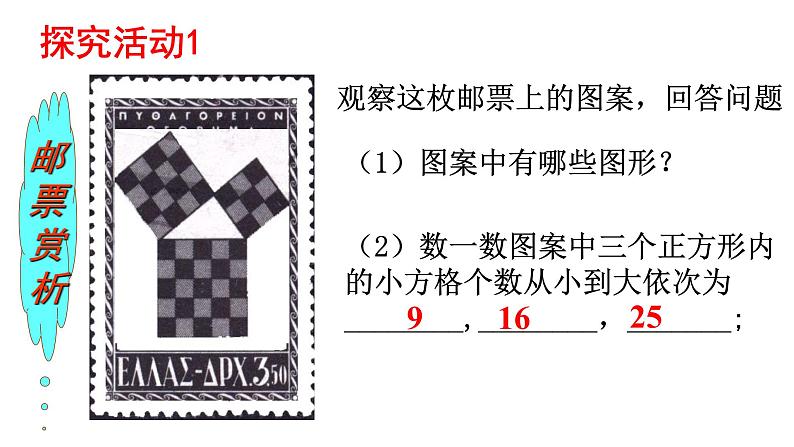
1955年希腊为纪念数学家毕达哥拉斯发行的邮票。
（2）数一数图案中三个正方形内的小方格个数从小到大依次为________,________，_______;
观察这枚邮票上的图案，回答问题
（1）图案中有哪些图形？
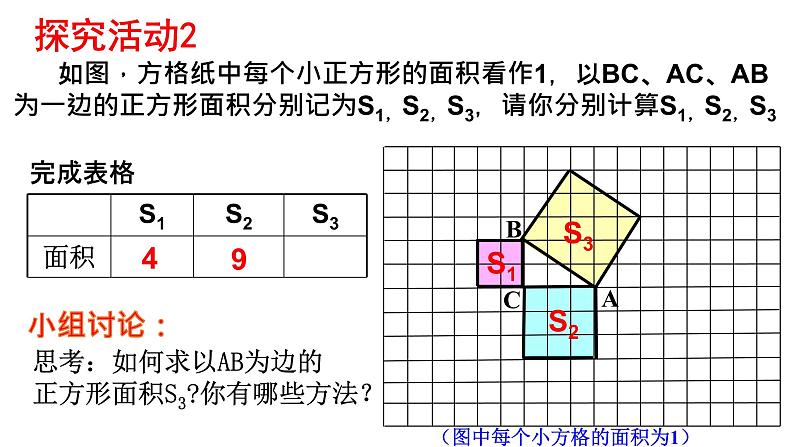
如图，方格纸中每个小正方形的面积看作1，以BC、AC、AB为一边的正方形面积分别记为S1，S2，S3，请你分别计算S1，S2，S3
（图中每个小方格的面积为1）
思考：如何求以AB为边的正方形面积S3?你有哪些方法？
（1）分别求出图中三个正方形的面积S1,S2,S3
（2）猜想S1,S2,S3之间有怎样的数量关系
S1=___ S2=___ S3=___
S1=___ S2=___S3=___
刚才所选取的直角三角形都放置在网格中，且两直角边长度都为整数，下面老师用几何画板演示一下各边为任意一个数值的情况
如图， △ ABC和△ DEF都不是直角三角形，分别以三角形三边为一边向外作正方形，将他们的面积从小到大依次记为S1,S2,S3,那么S1+S2=S3还成立吗？小组合作探究。
（图中每个小方格代表一个单位面积）
S1=___ S2=___S3=___
以直角三角形两直角边为边长的正方形面积之和等于以斜边为边长的正方形面积
如果直角三角形的两直角边的长分别为a和b，斜边长为c　
（2）你能发现直角三角形三边 长度之间存在什么关系吗？
（3）你能用文字语言描述吗？
(1).用a,b,c来表示这3个正方形的面积。
直角三角形两直角边a、b的平方和等于斜边c的平方。
几何语言：在Rt△ ABC中，∠C=90°
BC2+AC2=AB2
古人把弯曲成直角的手臂的上半部分称为“勾”，下半部分称为“股”，我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.因此就把这一定理称为勾股定理.
我国是最早了解勾股定理的国家之一. 早在三千多年前，周朝的数学家商高就提出，将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”. 它被记载于我国古代著名的数学著作《周髀算经》中. 在这本书中的另一处，还记载了勾股定理的一般形式. 这一发现，至少早于古希腊人500多年. 作为一名中国人，我们应为我国古人的博学和多思而感到自豪！　
1.求下列直角三角形中未知边的长:
x2+82 =17 2
2.求下列图中表示边的未知数x、y的值.
① x=______
② y=_______
3．在如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，若最大正方形的面积为9cm2，则正方形a，b的面积之和是　 　cm2．
若最大正方形的面积为9cm2，则正方形c,d,e,f的面积之和是　 cm2．
穿越草坪走“近道”，既踏秃 了草坪，又丑化了生活的环境。
小明实际上只少走了几米的距离？
爱护环境 人人有责
我有哪些收获呢？与大家共分享！
学 而 不 思 则 罔
1．如图，带阴影的正方形面积是　 　．
2、如图，受台风影响，一棵树在离地面4米处断裂，树的顶部落在离树跟底部3米处，这棵树折断前有多高？
3.如图，已知AB=3，AC=4,CD=13,∠A= ∠CBD=900,求BC、BD的长。