2021学年第十一章 三角形综合与测试同步训练题

这是一份2021学年第十一章 三角形综合与测试同步训练题，共12页。
1．下列长度的各组线段不能组成一个三角形的是（ ）
A．2cm，2cm，1cmB．2cm，2cm，2cm
C．2cm，2cm，3cmD．2cm，2cm，4cm
2．下列各图中，作△ABC边AC上的高，正确的是（ ）
A．B．
C．D．
3．如图，要使五边形木架不变形，至少要再钉上几根木条（ ）
A．1根B．2根C．3根D．4根
4．下列角度中，不能成为多边形内角和的是（ ）
A．600°B．720°C．900°D．1080°
5．已知一个多边形的外角都等于40°，那么这个多边形的边数为（ ）
A．6B．7C．8D．9
6．如图，CE是△ABC的外角∠ACD的平分线，若∠B＝35°，∠ACE＝60°，则∠A＝（ ）
A．95°B．85°C．75°D．65°
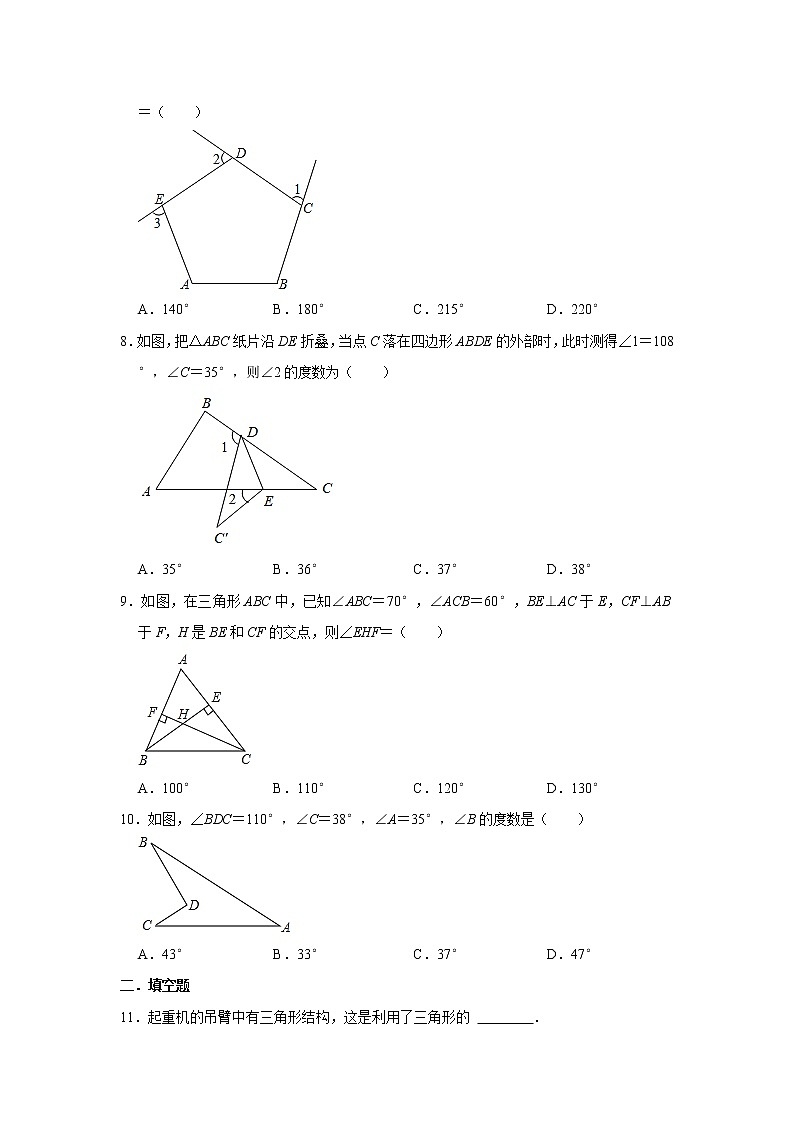
7．如图∠1，∠2，∠3是五边形ABCDE的三个外角，若∠A+∠B＝215°，则∠1+∠2+∠3＝（ ）
A．140°B．180°C．215°D．220°
8．如图，把△ABC纸片沿DE折叠，当点C落在四边形ABDE的外部时，此时测得∠1＝108°，∠C＝35°，则∠2的度数为（ ）
A．35°B．36°C．37°D．38°
9．如图，在三角形ABC中，已知∠ABC＝70°，∠ACB＝60°，BE⊥AC于E，CF⊥AB于F，H是BE和CF的交点，则∠EHF＝（ ）
A．100°B．110°C．120°D．130°
10．如图，∠BDC＝110°，∠C＝38°，∠A＝35°，∠B的度数是（ ）
A．43°B．33°C．37°D．47°
二．填空题
11．起重机的吊臂中有三角形结构，这是利用了三角形的 ．
12．若一个三角形的两边长分别是2cm和9cm，且第三边为奇数，则第三边长为 ．
13．一个正多边形，它的一个内角等于一个外角的2倍，那么这个正多边形的边数是 ．
14．如图，在△ABC中，∠BAC＝60°，BD、CE分别平分∠ABC、∠ACB，BD、CE相交于点O，则∠BOC的度数是 ．
15．如图，小明从点A出发，前进5m后向右转20°，再前进5m后又向右转20°，这样一直走下去，直到他第一次回到出发点A为止，他所走的路径构成了一个多边形，则这个多边形的内角和是 度．
16．在△ABC中，AM是BC边上的中线，已知AB﹣AC＝5，且△AMC的周长是20，则△ABM的周长是 ．
17．如图所示，△ABC中∠C＝80°，AC边上有一点D，使得∠A＝∠ABD，将△ABC沿BD翻折得△A′BD，此时A′D∥BC，则∠ABC＝ 度．
三．解答题
18．一个多边形的内角和比外角和的多780°，它是几边形？
19．如图，∠1，∠2，∠3，∠4是四边形ABCD的四个外角．用两种方法证明∠1+∠2+∠3+∠4＝360°．
20．在△ABC中，∠BAC＝50°，∠B＝48°，AD是△ABC的角平分线，求∠ADC的度数．
21．如图，AD是△ABC的BC边上的高，AE平分∠BAC，若∠B＝42°，∠C＝72°，求∠AEC和∠DAE的度数．
22．如图，在△ABC中，∠ABC和∠ACB的平分线相交于点P．
（1）若∠ABC+∠ACB＝130°，求∠BPC的度数．
（2）当∠A为多少度时，∠BPC＝3∠A？
23．如图，把△ABC沿EF折叠，使点A落在点D处，
（1）若DE∥AC，试判断∠1与∠2的数量关系，并说明理由；
（2）若∠B+∠C＝130°，求∠1+∠2的度数．
24．图1，线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”．如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试解答下列问题：
（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系： ；
（2）图2中，当∠D＝50度，∠B＝40度时，求∠P的度数．
（3）图2中∠D和∠B为任意角时，其他条件不变，试问∠P与∠D、∠B之间存在着怎样的数量关系．
参考答案
一．选择题
1．解：A、∵2+1＞2，∴能组成三角形；
B、∵2+2＞2，∴能组成三角形；
C、∵2+2＞3，∴能组成三角形；
D、∵2+2＝4，∴不能组成三角形．
故选：D．
2．解：A、AD是△ABC边BC上的高，不符合题意；
B、AD是△ADC边AC上的高，不符合题意；
C、BD是△DBC边BC上的高，不符合题意；
D、BD是△ABC边AC上的高，符合题意；
故选：D．
3．解：如图，根据三角形的稳定性可知，要使五边形木架不变形，至少要再钉上2根木条，
故选：B．
4．解：∵600不是180的倍数，∴600°不能成为多边形的内角和，故A选项符合题意；
∵720是180的倍数，∴720°能成为多边形的内角和，故B选项不符合题意；
∵900是180的倍数，∴900°能成为多边形的内角和，故C选项不符合题意；
∵1080是180的倍数，∴1080°能成为多边形的内角和，故D选项不符合题意．
故选：A．
5．解：由题意得360°÷40°＝9，
∴四边形的边数为9．
故选：D．
6．解：∵CE是∠ACD的平分线，∠ACE＝60°，
∴∠ACD＝2∠ACE＝120°，
∵∠ACD是△ABC的外角，
∴∠A＝∠ACD﹣∠B＝120°﹣35°＝85°，
故选：B．
7．解：五边形ABCDE的内角和为（5﹣2）×180°＝540°，
∵∠A+∠B＝215°，
∴∠AED+∠EDC+∠BCD＝540°﹣215°＝325°，
又∵∠AED+∠EDC+∠BCD+∠1+∠2+∠3＝180°×3＝540°，
∴∠1+∠2+∠3＝540°﹣325°＝215°．
故选：C．
8．解：如图，设C′D与AC交于点O，
∵∠C＝35°，
∴∠C′＝∠C＝35°，
∵∠1＝∠DOC+∠C，∠1＝108°，
∴∠DOC＝∠1﹣∠C＝108°﹣35°＝73°，
∵∠DOC＝∠2+∠C′，
∴∠2＝∠DOC﹣∠C′＝73°﹣35°＝38°．
故选：D．
9．解：∵∠ABC＝70°，∠ACB＝60°，
∴∠A＝180°﹣∠ABC﹣∠ACB＝50°，
∵BE⊥AC，CF⊥AB，
∴∠CFB＝∠AEB＝90°，
∴∠ABE＝90°﹣∠A＝40°，
∵∠EHF是△BFH的一个外角，
∴∠EHF＝∠CFB+∠ABE＝130°．
故选：D．
10．解：如图，延长CD交AB于E，
∵∠C＝38°，∠A＝35°，
∴∠1＝∠C+∠A＝38°+35°＝73°，
∵∠BDC＝110°，
∴∠B＝∠BDC﹣∠1＝110°﹣73°＝37°．
故选：C．
二．填空题
11．解：起重机的吊臂中有三角形结构，这是利用了三角形的稳定性．
故答案为：稳定性．
12．解：设第三边长xcm．
根据三角形的三边关系，得7＜x＜11．
又∵三角形的第三边长是奇数，因而满足条件的数是9cm．
故答案为：9cm．
13．解：设正多边形的一个外角的度数为x°，
由题意得2x+x＝180°，
解得x＝60，
360°÷60°＝6，
所以这个正多边形的边数是6．
故答案为6．
14．解：∵∠BAC＝60°，BD，CE分别平分∠ABC，∠ACB，
∴∠BOC＝180°﹣（∠ABC+∠ACB）＝180°﹣（180°﹣60°）＝120°，
故答案为：120°．
15．解：由题意知，该多边形为正多边形，
∵多边形的外角和恒为360°，
360÷20＝18，
∴该正多边形为正18边形．
这个多边形的内角和为：（18﹣2）×180°＝2880°，
故答案为：2880．
16．解：∵AM是BC边上的中线，
∴BM＝MC，
∵△AMC的周长是20，AB﹣AC＝5，
∴AM+AC+MC＝AM+AB﹣5+BM＝20，
∴AM+AB+BM＝25，
则△ABM的周长＝AM+AB+BM＝25，
故答案为：25．
17．解：设∠A＝∠ABD＝x，
∵△ABC沿BD翻折得△A′BD，
∴∠A＝∠DBA′＝∠A′＝∠ABD＝x，
∵A′D∥BC，
∴∠A′＝∠CBA′＝x，
∴∠CBA＝∠CBA′+∠A′BD+∠ABD＝3x，
由三角形内角和定理得，
∠A+∠ABC+∠C＝180°，
x+3x+80°＝180°，
x＝25°，
∴3x＝3×25°＝75°，
故答案为：75．
三．解答题
18．解：设它是n边形，
根据题意得：（ n﹣2）×180°﹣360°×＝780°，
解得：n＝7．
答：它是七边形．
19．证法1：
∵∠1+∠BAD＝180°，∠2+∠ABC＝180°，∠3+∠BCD＝180°，∠4+∠CDA＝180°，
∴∠1+∠BAD+∠2+∠ABC+∠3+∠BCD+∠4+∠CDA＝180°×4＝720°．
∵∠BAD+∠ABC+∠BCD+∠CDA＝360°，
∴∠1+∠2+∠3+∠4＝360°．
证法2：连接BD，
∵∠1＝∠ABD+∠ADB，∠3＝∠CBD+∠CDB，
∴∠1+∠2+∠3+∠4＝∠ABD+∠ADB+∠2+∠CBD+∠CDB+∠4＝180°×2＝360°．
20．解：∵∠BAC＝50°，∠B＝48°，
∴∠C＝180°﹣∠BAC﹣∠B＝82°，
∵AD是△ABC的角平分线，
∴∠CAD＝∠BAC＝25°，
∴∠ADC＝180°﹣∠CAD﹣∠C＝73°．
21．解：∵∠BAC+∠B+∠C＝180°，∠B＝42°，∠C＝72°，
∴∠BAC＝66°，
∵AE平分∠BAC，
∴∠BAE＝∠CAE＝∠BAC＝33°，
∴∠AEC＝∠B+∠BAE＝75°，
∵AD⊥BC，
∴∠ADE＝90°，
∴∠DAE＝90°﹣∠AEC＝15°．
22．解：（1）∵PB为∠ABC的平分线，PC为∠ACB的平分线，
∴∠PBC+∠PCB＝（∠ABC+∠ACB）＝65°．
在△PBC中，∠PBC+∠PCB＝65°，
∴∠BPC＝180°﹣（∠PBC+∠PCB）＝115°．
（2）由（1）可知：∠BPC＝180°﹣（∠ABC+∠ACB），
∴∠BPC＝180°﹣（180°﹣∠A）＝90°+A．
设∠A＝α，
∴90°+，
解得α＝36°，
∴∠A＝36°．
23．解：（1）∠1＝∠2，理由如下：
∵∠D是由∠A翻折得到，
∴∠D＝∠A，
∵DE∥AC，
∴∠1＝∠A，∠2＝∠D，
∴∠1＝∠2．
（2）∵∠A+∠B+∠C＝180°，∠A+∠AEF+∠AFE＝180°，
∴∠AEF+∠AFE＝∠B+∠C＝130°，
∵△DEF是△AEF由翻折得到，
∵∠AED＝2∠AEF，∠AFD＝2∠AFE，
∴∠AED+∠AFD＝260°，
∵∠1+∠2+∠AED+∠AFD＝360°，
∴∠1+∠2＝100°．
24．解：（1）由题知，∠A+∠D＝∠DOB＝∠C+∠B，
∴∠A+∠D＝∠C+∠B，
故答案为：∠A+∠D＝∠C+∠B；
（2）由（1）可得，∠DAO+∠D＝∠OCB+∠B，①
同理可得，∠DAM+∠D＝∠OCP+∠P，
∵∠DAB和∠BCD的平分线是AP和CP，
∴∠DAO+∠D＝∠OCB+∠P，②
由②×2﹣①得，∠D＝2∠P﹣∠B，
即2∠P＝∠D+∠B，
∴2∠P＝50°+40°，
故∠P＝45°；
（3）由（2）可知2∠P＝∠B+∠D．