福建省福州市2020-2021学年八年级下学期期中考试数学试卷（word版 含答案）

这是一份福建省福州市2020-2021学年八年级下学期期中考试数学试卷（word版 含答案），共10页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．下列解析式中，y不是x的函数的是（ ）
A．y＝2xB．y＝x2C．y＝± （x＞0）D．y＝|x|
2．下列计算正确的是（ ）
A．B．
C．D．
3．矩形、菱形、正方形都具有的性质是（ ）
A．对角线相等B．对角线互相平分
C．对角线互相垂直D．对角线平分对角
4．已知关于x的方程有一个根是，则的值为（ ）
A．B．0C．1D．2
5．一次函数y=kx+b中，y随x的增大而减小，b0，则这个函数的图象不经过（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
6．已知△ABC的三边分别为a，b，c，下列条件无法判定△ABC是直角三角形的是（ ）
A．B．
C．D．
7．如图，在四边形中，对角线相交于点O，下列条件不能判定这个四边形是平行四边形的是（ ）
A．B．
C．D．
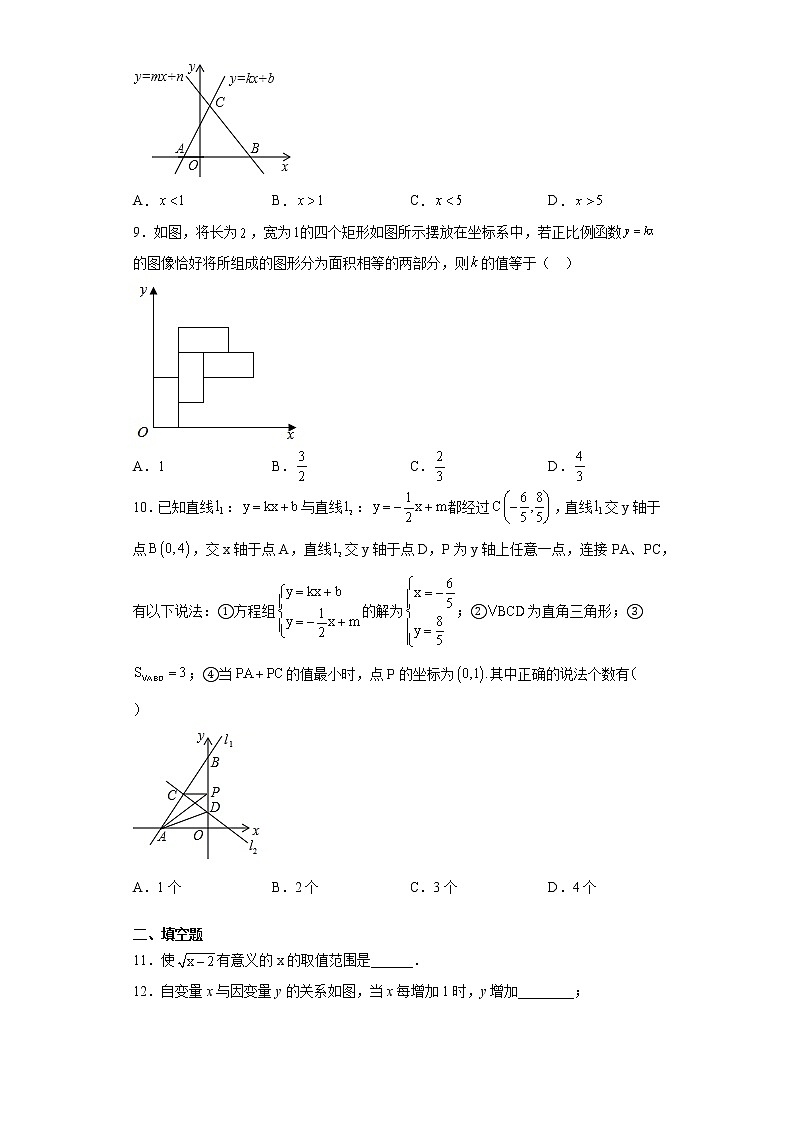
8．如图，直线与直线相交于点，则不等式的解集为（ ）
A．B．C．D．
9．如图，将长为，宽为的四个矩形如图所示摆放在坐标系中，若正比例函数的图像恰好将所组成的图形分为面积相等的两部分，则的值等于（ ）
A．B．C．D．
10．已知直线：与直线：都经过，直线交y轴于点，交x轴于点A，直线交y轴于点D，P为y轴上任意一点，连接PA、PC，有以下说法：①方程组的解为；②为直角三角形；③；④当的值最小时，点P的坐标为其中正确的说法个数有
A．1个B．2个C．3个D．4个
二、填空题
11．使有意义的x的取值范围是______．
12．自变量x与因变量y的关系如图，当x每增加1时，y增加________；
13．若一元二次方程有两个相等的实数根，则______．
14．明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》：“平地秋千未起，踏板一尺离地，送行二步恰竿齐，五尺板高离地…”翻译成现代文为：如图，秋千OA静止的时候，踏板离地高一尺（尺），将它往前推进两步（尺），此时踏板升高离地五尺（尺），则秋千绳索（OA或OB）的长度为______尺．
15．如图，△ACB和△ECD都是等腰直角三角形，，，△ACB的顶点A在△ECD的斜边DE上，若，，则AD的长是______．
16．如图，中，//轴，．点A的坐标为，点D的坐标为，点B在第四象限，点G是AD与y轴的交点，点P是CD边上不与点C，D重合的一个动点，过点P作y轴的平行线PM，过点G作x轴的平行线GM，它们相交于点M，将△PGM沿直线PG翻折，当点M的对应点落在坐标轴上时，点P的坐标为______．
三、解答题
17．解方程：
（1） （2）
18．化简并求值：，其中．
19．在如图所示的方格纸中，每个小正方形的边长为个单位长度，我们称每个小正方形的顶点为“格点”．
（1）若格点在线段右侧，且满足，则当的周长最小时，的面积等于 ．
（2）若格点在线段左侧，且满足，则的面积等于 (以上两问均直接写出结果即可）．
20．如图，中，点E在BC上，且，试分别在下列两个图中按要求使用无刻度直尺画图．（保留作图痕迹）
（1）在图1中，画出的平分线；
（2）在图2中，画出的平分线，并说明理由．
21．阅读下列内容：设a，b，c是一个三角形的三条边的长，且a是最长边，我们可以利用a，b，c三条边长度之间的关系来判断这个三角形的形状：
①若，则该三角形是直角三角形；
②若，则该三角形是钝角三角形；
③若，则该三角形是锐角三角形．
例如：若一个三角形的三边长分别是4，5，6，则最长边是6，，故由③可知该三角形是锐角三角形；请解答以下问题：
（1）若一个三角形的三边长分别是7，8，9，则该三角形是_______三角形；
（2）若一个三角形的三边长分别是3，4，x，且这个三角形是直角三角形，则x的值_____；
（3）若一个三角形的三边长为，，，其中a是最长边，请判断这个三角形的形状，并写出你的判断过程．
22．如图，在正方形ABCD中，P为对角线BD上一点，过点P作，，垂足分别为E，F．
（1）求证：四边形PECF为矩形；
（2）试探究与EF的数量关系，并说明理由，
23．甲，乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地，轿车比货车晚出发1.5小时，如图，线段OA表示货车离甲地的距离y（千米）与时间x（小时）之间的函数关系；折线BCD表示轿车离甲地的距离y（千米）与时间x（时）之间的函数关系，线段CD对应的函数解析式是，
（1）由图像可得，货车的速度为______千米/时；轿车在行驶到点C之前，轿车的速度为____千米/时；
（2）在轿车行进过程中，轿车行驶多少时间，两车相距15千米？
24．已知：在矩形ABCD中，，．
（1）如图1，E、F、G、H分别是AD，AB，BC，CD的中点、求证：四边形EFGH是菱形；
（2）如图2，若菱形EFGH的三个顶点E、F、H分别在AD，AB，CD上，．
①连接BG，若，求AF的长；
②设，△GFB的面积为S，且S满足函数关系式．在自变量m的取值范围内，是否存在m，使菱形EPGH面积最大？若存在，请直接写出菱形EFGH面积最大值，若不存在，请说明理由．
25．如图1，在平面直角坐标系中，过点的两条直线分别交y轴于B、C两点，且B、C两点的纵坐标分别是一元二次方程的两个根．
（1）判断直线AC与直线AB的位置关系？并说明理由；
（2）如图2，若点D在直线AC上，且△BCD为等边三角形，动点E在直线AC上（不与点D、C重合），做直线BD，垂足为点F，设点EF的长为d，点E的横坐标是x，请求出d与x的函数关系式：
（3）在（2）的条件下，直线BD上是否存在点P，平面内是否存在点Q，使以A、B、P、Q四点为顶点的四边形是菱形，若存在请直接写出点Q的坐标；若不存在，请说明理由．
参考答案
1．C
2．D
3．B
4．A
5．A
6．B
7．C
8．B
9．D
10．D
11．
12．2
13．
14．14.5
15．6
16．，或，
17．（1），；（2），
18．，
19．（1）2.5；（2）2或2.5或1.5
20．（1）略；（2）略
21．（1）锐角；（2）5或；（3）略
22．（1）略；（2）AP=EF
23．（1）60，80；（2）轿车行进过程中，轿车行驶2.1小时或2.7小时时，两车相距15千米
24．（1）略；（2）①；②存在m=，菱形EFGH面积最大为
25．（1）AB⊥AC；（2）；（3）或，或，或，