山东省淄博市沂源县2020-2021学年八年级下学期期末数学试题(word版 含答案)
展开一、单选题
1.下列计算正确的是( )
A.B.C.D.
2.已知m,n是关于x的一元二次方程的两个解,若,则a的值为( )
A.﹣10B.4C.﹣4D.10
3.已知关于的方程,下列说法正确的是
A.当时,方程无解
B.当时,方程有一个实数解
C.当时,方程有两个相等的实数解
D.当时,方程总有两个不相等的实数解
4.已知一元二次方程的较小根为x1,则下面对x1的估计正确的是
A.B.C.D.
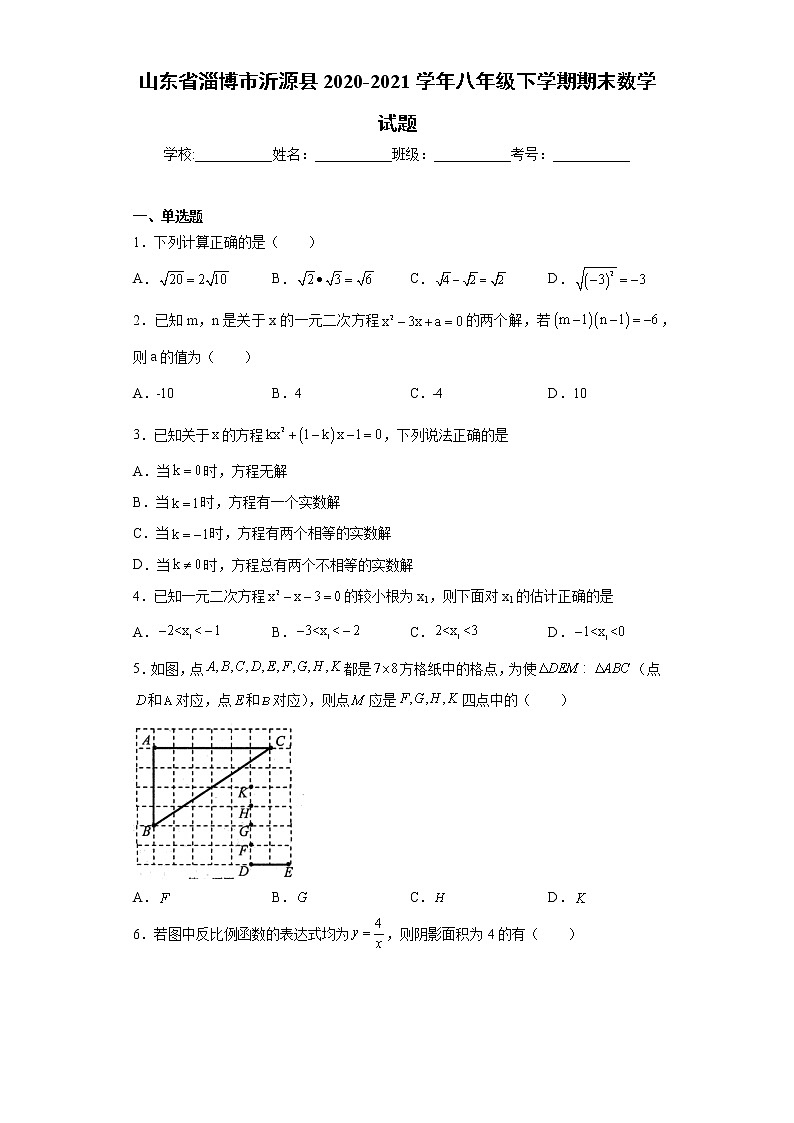
5.如图,点都是方格纸中的格点,为使(点和对应,点和对应),则点应是四点中的( )
A.B.C.D.
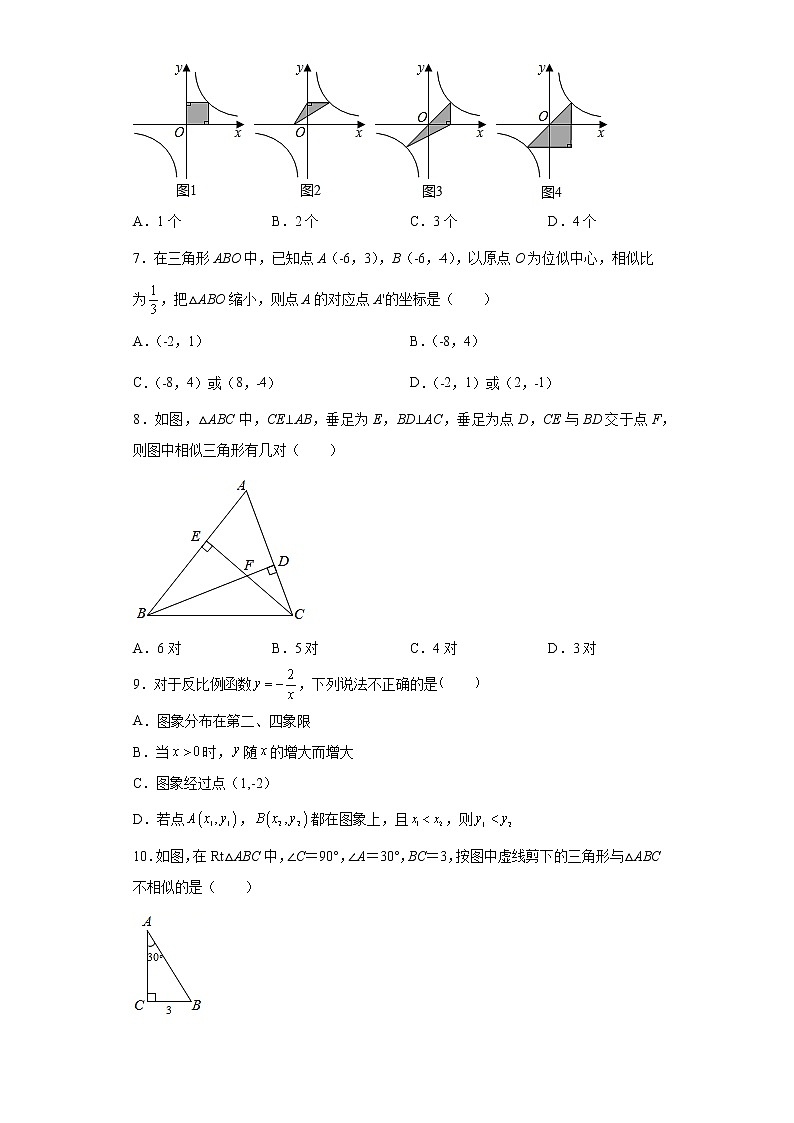
6.若图中反比例函数的表达式均为,则阴影面积为4的有( )
A.1个B.2个C.3个D.4个
7.在三角形ABO中,已知点A(﹣6,3),B(﹣6,﹣4),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A'的坐标是( )
A.(﹣2,1)B.(﹣8,4)
C.(﹣8,4)或(8,﹣4)D.(﹣2,1)或(2,﹣1)
8.如图,△ABC中,CE⊥AB,垂足为E,BD⊥AC,垂足为点D,CE与BD交于点F,则图中相似三角形有几对( )
A.6对B.5对C.4对D.3对
9.对于反比例函数,下列说法不正确的是
A.图象分布在第二、四象限
B.当时,随的增大而增大
C.图象经过点(1,-2)
D.若点,都在图象上,且,则
10.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=3,按图中虚线剪下的三角形与△ABC不相似的是( )
A.B.C.D.
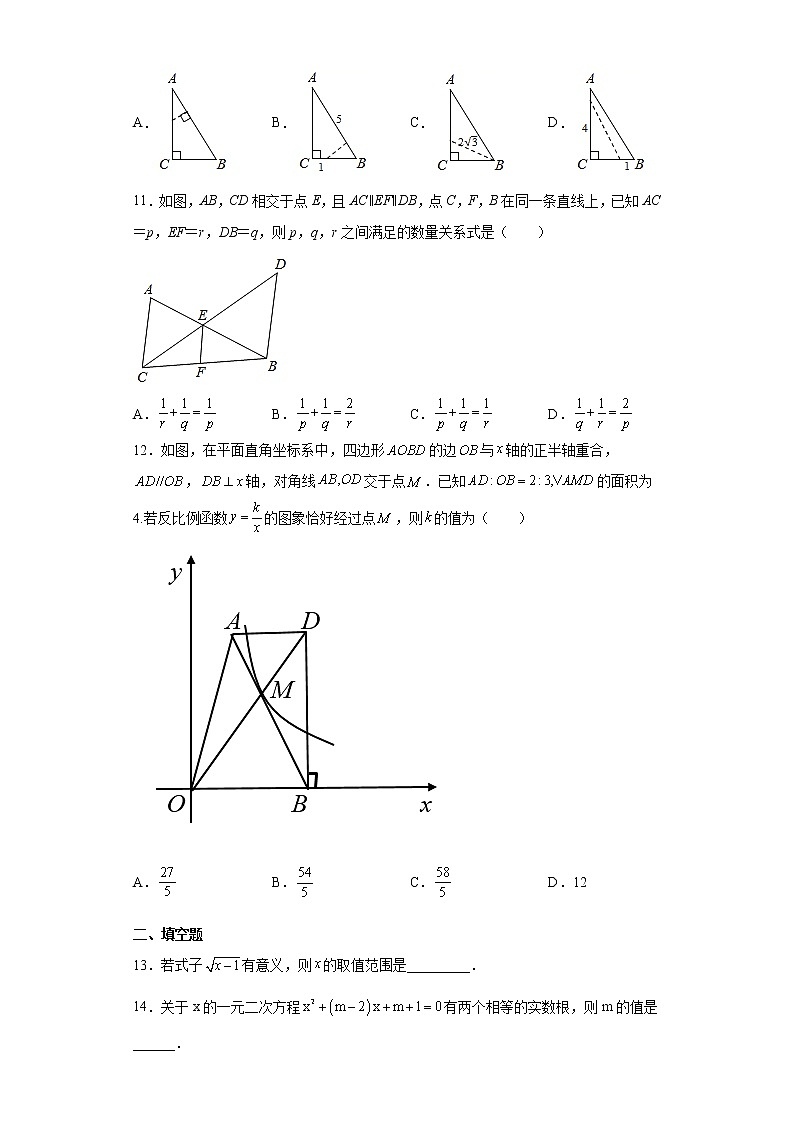
11.如图,AB,CD相交于点E,且AC∥EF∥DB,点C,F,B在同一条直线上,已知AC=p,EF=r,DB=q,则p,q,r之间满足的数量关系式是( )
A.B.C.D.
12.如图,在平面直角坐标系中,四边形的边与轴的正半轴重合,,轴,对角线交于点.已知的面积为4.若反比例函数的图象恰好经过点,则的值为( )
A.B.C.D.12
二、填空题
13.若式子有意义,则的取值范围是_________.
14.关于x的一元二次方程有两个相等的实数根,则m的值是______.
15.若正数a是一元二次方程x2﹣5x+m=0的一个根,﹣a是一元二次方程x2+5x﹣m=0的一个根,则a的值是______.
16.如图,已知两个反比例函数C1:y=和C2:y=在第一象限内的图象,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为_____.
17.如图,小明用相似图形的知识测量旗杆高度,已知小明的眼睛离地面1.5米,他将3米长的标杆竖直放置在身前3米处,此时小明的眼睛、标杆的顶端、旗杆的顶端在一条直线上,通过计算测得旗杆高度为15米,则旗杆和标杆之间距离CE长___________米.
三、解答题
18.求代数式a的值,其中a=1007,如图是小亮和小芳的解答过程:
(1) 的解法是错误的;
(2)求代数式a的值,其中a=﹣2021.
19.已知关于x的方程x2−2(k−3)x+k2−4k−1=0.
(1)若这个方程有实数根,求k的取值范围;
(2)若以方程x2−2(k−3)x+k2−4k−1=0的两个根为横坐标、纵坐标的点恰在反比例函数的图象上,求满足条件的m的最小值.
20.如图:△PQR是等边三角形,∠APB=120°.求证:QR2=AQ•RB.
21.如图,反比例函数(x>0,k为常数)的图象经过点A(1,4),点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
(1)写出反比例函数解析式;
(2)求证:△ACB∽△NOM;
(3)若△ACB与△NOM的相似比为2,求出B点的坐标.
22.为更好地发展低碳经济,建设美丽中国.某公司对其生产设备进行了升级改造,不仅提高了产能,而且大幅降低了碳排放量.已知该公司去年第三季度产值是2300万元,今年第一季度产值是3200万元,假设公司每个季度产值的平均增长率相同.
(1)求该公司每个季度产值的平均增长率;
(2)问该公司今年总产值能否超过1.6亿元?并说明理由.
23.已知:在正方形ABCD的边BC上任取一点F,连接AF,一条与AF垂直的直线l(垂足为点P)沿AF方向,从点A开始向下平移,交边AB于点E.
(1)当直线l经过AF的中点时,与对角线BD交于点Q,连接FQ,如图2所示,求∠AFQ的度数;
(2)直线l继续向下平移,当点P恰好落在对角线BD上时,交边CD于点G,设AB=2,BF=x,DG=y,求y与x之间的关系式.
24.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ:S△ABC=9:100?若存在,求出t的值;若不存在,说明理由.
(3)当t为何值时,△CPQ为等腰三角形?
可能用到的数据
计算结果(已取近似值)
1.18
1.182
1.39
1.183
1.64
参考答案
1.B
2.C
3.C
4.A
5.C
6.B
7.D
8.A
9.D
10.D
11.C
12.B
13.
14.0或8
15.5
16.
17.24
18.(1)小亮;(2)-a+6,2027
19.(1)k≤5;(2)-5
20.略
21.(1),(2)略,(3)
22.(1)该公司每个季度产值的平均增长率为18%;(2)该公司今年总产值能超过1.6亿元,理由见解析
23.(1)45°;(2)(0≤x≤2)
24.(1)线段CD的长为4.8;(2)S△CPQ=﹣t2+t;当t=秒或t=3秒时,S△CPQ:S△ABC=9:100.(3)当t为2.4秒或秒或秒时,△CPQ为等腰三角形.
2020-2021学年山东省淄博市沂源县八年级上学期期中数学试题及答案: 这是一份2020-2021学年山东省淄博市沂源县八年级上学期期中数学试题及答案,共14页。试卷主要包含了选择题.,填空题.,解答题等内容,欢迎下载使用。
山东省淄博市沂源县2021-2022学年六年级下学期期末数学试题(word版含答案): 这是一份山东省淄博市沂源县2021-2022学年六年级下学期期末数学试题(word版含答案)
山东省淄博市沂源县2021-2022学年七年级下学期期末数学试题(word版含答案): 这是一份山东省淄博市沂源县2021-2022学年七年级下学期期末数学试题(word版含答案),共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












