




所属成套资源:2022版新高考数学人教版一轮课件(共72份)
2022版新高考数学人教版一轮课件:第7章 第7讲 立体几何中的向量方法
展开
这是一份2022版新高考数学人教版一轮课件:第7章 第7讲 立体几何中的向量方法,共60页。
第七讲 立体几何中的向量方法
1 知识梳理·双基自测
2 考点突破·互动探究
3 名师讲坛·素养提升
知识点一 两个重要的向量(1)直线的方向向量直线的方向向量是指和这条直线平行(或重合)的非零向量,一条直线的方向向量有_______个.(2)平面的法向量直线l⊥平面α,取直线l的方向向量,则这个向量叫做平面α的法向量.显然一个平面的法向量有_______个,它们是共线向量.
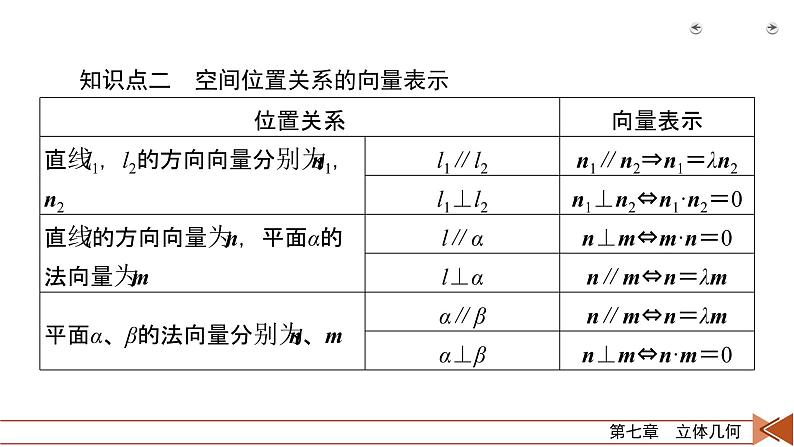
知识点二 空间位置关系的向量表示
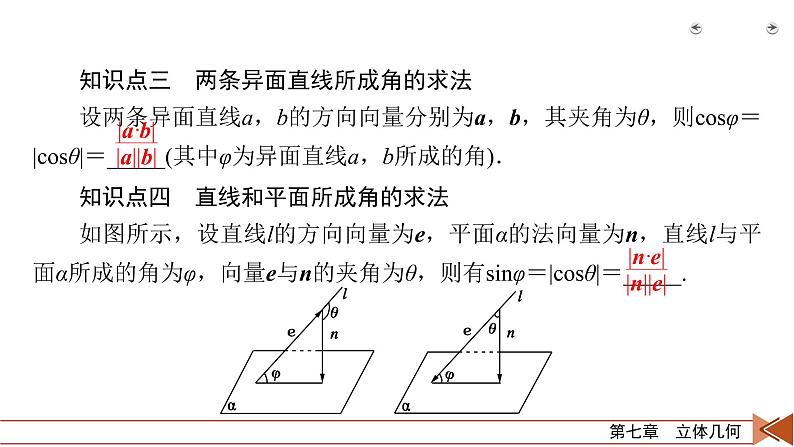
知识点三 两条异面直线所成角的求法设两条异面直线a,b的方向向量分别为a,b,其夹角为θ,则csφ=|csθ|=_____(其中φ为异面直线a,b所成的角).知识点四 直线和平面所成角的求法如图所示,设直线l的方向向量为e,平面α的法向量为n,直线l与平面α所成的角为φ,向量e与n的夹角为θ,则有sinφ=|csθ|=_____.
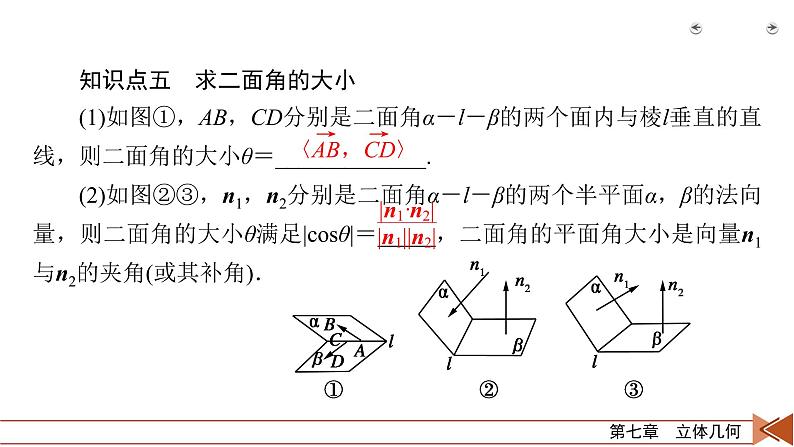
知识点五 求二面角的大小(1)如图①,AB,CD分别是二面角α-l-β的两个面内与棱l垂直的直线,则二面角的大小θ=_____________.(2)如图②③,n1,n2分别是二面角α-l-β的两个半平面α,β的法向量,则二面角的大小θ满足|csθ|=_____,二面角的平面角大小是向量n1与n2的夹角(或其补角).
题组一 走出误区1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)两直线的方向向量所成的角就是两条直线所成的角.( )(2)平面的单位法向量是唯一确定的.( )(3)若两平面的法向量平行,则两平面平行.( )(4)直线的方向向量和平面的法向量所成的角就是直线与平面所成的角.( )(5)两个平面的法向量所成的角是这两个平面所成的角.( )(6)若空间向最a平行于平面α,则a所在直线与平面a平行.( )
× × √ × × ×
题组二 走进教材2.(必修2P111T3)如图所示,在正方体ABCD-A1B1C1D1中,O是底面正方形ABCD的中心,M是D1D的中点,N是A1B1的中点,则直线ON,AM的位置关系是_______.
题组三 走向高考4.(2020·新高考Ⅰ)日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面,在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( )A.20° B.40° C.50° D.90°
[解析] 由题意作出如图所示的截面图,设所求角为α,由图易知α=40°,故选B.
5.(2019·浙江)如图,已知三棱柱ABC-A1B1C1,平面A1ACC1⊥平面ABC,∠ABC=90°,∠BAC=30°,A1A=A1C=AC,E,F分别是AC,A1B1的中点.(1)证明:EF⊥BC;(2)求直线EF与平面A1BC所成角的余弦值.
[解析] 解法一:(1)证明:连接A1E,因为A1A=A1C,E是AC的中点,所以A1E⊥AC,又平面A1ACC1⊥平面ABC,A1E⊂平面A1ACC1,平面A1ACC1∩平面ABC=AC,所以A1E⊥平面ABC,则A1E⊥BC.又因为A1F∥AB,∠ABC=90°,故BC⊥A1F.所以BC⊥平面A1EF.因此EF⊥BC.
解法二:(1)证明:连接A1E,因为A1A=A1C,E是AC的中点,所以A1E⊥AC.又平面A1ACC1⊥平面ABC,A1E⊂平面A1ACC1,平面A1ACC1∩平面ABC=AC,所以,A1E⊥平面ABC.如图,以点E为原点,分别以射线EC,EA1为y,z轴的正半轴,建立空间直角坐标系E-xyz.
(1)建立空间直角坐标时尽可能地利用图形中的垂直关系,要准确写出相关点的坐标,进而确定向量的坐标.(2)用向量法证平行问题的类型及常用方法
(3)利用向量法证垂直问题的类型及常用方法
〔变式训练1〕如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在线段BB1上,且EB1=1,D,F,G分别为CC1,C1B1,C1A1的中点.(1)求证:平面A1B1D⊥平面ABD;(2)求证:平面EGF∥平面ABD.
[解析] (1)证明:过点B作BO⊥AC于O.∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,BO⊂平面ABC,∴BO⊥平面PAC,∴BO⊥PA.又∵BC⊥平面PAB,PA⊂平面PAB,∴BC⊥PA.又∵BC∩BO=B,BC,BO⊂平面ABC,∴PA⊥平面ABC.
利用向量法确定二面角大小的常用方法(1)找法向量法:分别求出二面角的两个半平面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角的大小.(2)找与棱垂直的方向向量法:分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量,则这两个向量的夹角的大小就是二面角的大小.
〔变式训练2〕(1)(角度1)(2018·江苏高考题改编)在正三棱柱ABC-A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点,则异面直线BP与AC1所成角的余弦值为_____.
(3)(角度3)(2019·课标Ⅰ)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.①证明:MN∥平面C1DE;②求二面角A-MA1-N的正弦值.
[解析] (1)证明:取AD的中点O,连接OP,OB,BD,因为底面ABCD为菱形,∠BAD=60°,所以AD=AB=BD.因为O为AD的中点,所以BO⊥AD.在△PAD中,PA=PD,O为AD的中点,所以PO⊥AD.因为BO∩PO=O,所以AD⊥平面POB.因为PB⊂平面POB,所以AD⊥PB.
(2)因为平面A1ACC1⊥平面ABC,交线是AC,且C1M⊥AC,所以C1M⊥平面ABC.以M为原点,MB,MC,MC1分别为x,y,z轴建立空间直角坐标系,如图所示:
对于“是否存在”型问题的探索方式有两种:一种是根据条件作出判断,再进一步论证;另一种是利用空间向量,先设出假设存在点的坐标,再根据条件求该点的坐标,即找到“存在点”,若该点坐标不能求出,或有矛盾,则判定“不存在”.
[解析] (1)过点P在平面PAD内作PO⊥AD,垂足为O,连接BO、OC,∵平面PAD⊥平面ABCD,∴PO⊥平面ABCD,∴PO⊥BD,∵∠PDA=60°,PD=DA=2,∴△PDA是等边三角形,∴OD=1=BC,∵OD∥BC,∠BCD=90°,∴四边形OBCD是正方形,∴BD⊥OC,∵OC∩PO=O,∴BD⊥平面POC,∵PC⊂平面POC,∴BD⊥PC.
相关课件
这是一份高考数学一轮总复习课件第6章立体几何第7讲立体几何中的向量方法(含解析),共60页。PPT课件主要包含了图6-7-1,求二面角的大小,图6-7-2,名师点睛,线与平面所成的角,答案A,图6-7-4,A20°,B40°,C50°等内容,欢迎下载使用。
这是一份2024版高考数学一轮总复习第6章立体几何第7节立体几何中的向量方法__求空间角与距离课件,共60页。
这是一份高考数学一轮复习第6章第7节立体几何中的向量方法——求空间角与距离课件,共60页。










