高中数学人教版新课标B必修33.1.4概率的加法公式教案配套课件ppt

这是一份高中数学人教版新课标B必修33.1.4概率的加法公式教案配套课件ppt，共24页。PPT课件主要包含了要点归纳，专题一概率与频率，专题二古典概型，专题四几何概型，专题六数形结合思想等内容，欢迎下载使用。

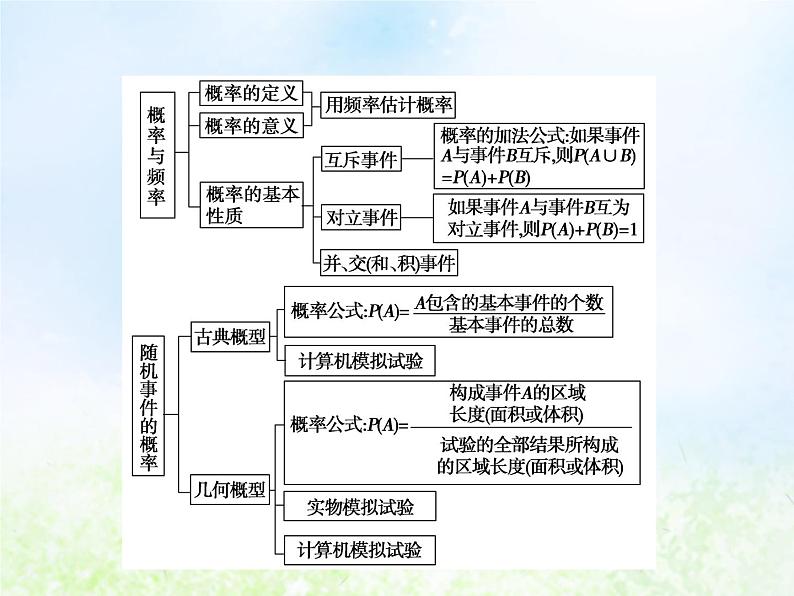
本章涉及的概念比较多，要真正理解它们的实质，搞清它们的区别与联系．了解随机事件发生的不确定性和频率的稳定性，要进一步了解概率的意义以及频率与概率的区别．
对于几何概型事件概率的计算，关键是求得事件A所占区域和整个区域的几何度量，然后代入公式求解．学习本章的过程中，要重视教材的基础作用，重视过程的学习，重视基本数学思想和数学方法的形成和发展，注意培养分析问题和解决问题的能力．
根据概率的统计定义，我们可以由频率来估计概率，因此应理清频率与概率的关系，频率是概率的近似值，是随机的，随着试验的不同而变化，而概率是多数次的试验中频率的稳定值，是一个常数，不要用一次或少数次试验中的频率来估计概率．
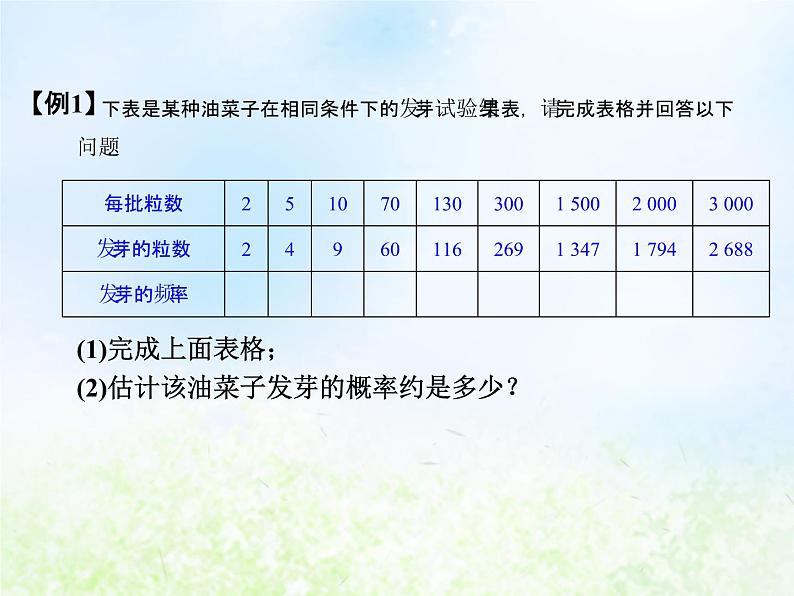
下表是某种油菜子在相同条件下的发芽试验结果表，请完成表格并回答以下问题.
(1)完成上面表格；(2)估计该油菜子发芽的概率约是多少？
某人一次同时抛出两枚均匀骰子(它们的六个面分别标有点数1、2、3、4、5、6)，(1)求两枚骰子点数相同的概率；(2)求两枚骰子点数之和为5的倍数的概率．解　用(x，y)表示同时抛出的两枚均匀骰子中一枚骰子向上的点数是x，另一枚骰子向上的点数是y，则全部结果有：(1,1)，(1,2)，(1,3)，(1,4)，(1,5)，(1,6)，(2,1)，(2,2)，(2,3)，(2,4)，(2,5)，(2,6)，(3,1)，(3,2)，(3,3)，(3,4)，(3,5)，(3,6)，(4,1)，(4,2)，(4,3)，(4,4)，(4,5)，(4,6)，(5,1)，(5,2)，(5,3)，(5,4)，(5,5)，(5,6)，(6,1)，(6,2)，(6,3)，(6,4)，(6,5)，(6,6)．即同时抛出两枚均匀骰子共有36种结果．则同时抛出两枚均匀骰子的结果是有限个，属于古典概型．
(2010·天津高考)有编号为A1，A2，…，A10的10个零件，测量其直径(单位：cm)，得到下面数据：
其中直径在区间[1.48,1.52]内的零件为一等品．(1)从上述10个零件中，随机抽取1个，求这个零件为一等品的概率．(2)从一等品零件中，随机抽取2个：①用零件的编号列出所有可能的抽取结果；②求这2个零件直径相等的概率．
互斥事件的概率加法公式是解决概率问题的重要公式，它能把复杂概率问题转化成较简单的基本事件的概率问题去解决或转化成求对立事件的概率问题，应用公式时一定要注意，首先确定各个事件是否彼此互斥，然后求出各事件分别发生的概率．
专题三　概率的加法公式
现有8名2010广州亚运会志愿者，其中志愿者A1，A2，A3通晓日语，B1，B2，B3通晓俄语，C1，C2通晓韩语，从中选出通晓日语、俄语和韩语的志愿者各1名，组成一个小组．(1)求A1被选中的概率；(2)求B1和C1不全被选中的概率．解　(1)从8人中选出日语、俄语和韩语的志愿者各1名，其一切可能的结果组成的基本事件空间Ω＝{(A1，B1，C1)，(A1，B1，C2)，(A1，B2，C1)，(A1，B2，C2)，(A1，B3，C1)，(A1，B3，C2)，(A2，B1，C1)，(A2，B1，C2)，(A2，B2，C1)，(A2，B2，C2)，(A2，B3，C1)，(A2，B3，C2)，(A3，B1，C1)，(A3，B1，C2)，(A3，B2，C1)，(A3，B2，C2)，(A3，B3，C1)，(A3，B3，C2)}，即由18个基本事件组成．由于每一个基本事件被抽取的机会均等，因此这些基本事件的发生是等可能的．
几何概型同古典概型一样，是概率中最具有代表性的试验概型之一，在高考命题中占有非常重要的位置．我们要理解并掌握几何概型试验的两个基本特征，即：每次试验中基本事件的无限性和每个事件发生的等可能性，并能求简单的几何概型试验的概率．
统计和古典概型的综合是高考解答题的一个命题趋势和热点，此类题很好地结合了统计与概率的相关知识，并且在实际生活中应用也十分广泛，能很好地考查学生的综合解题能力，在解决综合问题时，要求同学们对图表进行观察、分析、提炼、挖掘出图表所给予的有用信息，排除有关数据的干扰，进而抓住问题的实质，达到求解的目的．
专题五　概率与统计的综合问题
随机抽取某中学甲、乙两班各10名同学，测量他们的身高(单位：cm)，获得身高数据的茎叶图如图所示．
(1)根据茎叶图判断哪个班的平均身高较高；(2)计算甲班的样本方差；(3)现从乙班这10名同学中随机抽取两名身高不低于173 cm的同学，求身高为176 cm的同学被抽中的概率．
数形结合思想在本章的应用很广泛，如用集合的关系与运算表示事件的关系与运算，用图表的形式表示一次试验的基本事件以及几何概型中画图表示问题中涉及的量，从而求出事件的概率．
设M＝{1,2,3,4,5,6,7,8,9,10}，任取x，y∈M，x≠y.求x＋y是3的倍数的概率．解　利用平面直角坐标系列举，如图所示．