初中数学人教版八年级上册第十二章 全等三角形综合与测试单元测试测试题

这是一份初中数学人教版八年级上册第十二章 全等三角形综合与测试单元测试测试题，共8页。

一．选择题（每小题3分，共30分）
1．如图，已知OC平分∠AOB，P是OC上一点，PH⊥OB于H，若PH＝5，则点P与射线OA上某一点连线的长度可以是（ ）
A．6B．4C．3D．2
2．如图，点B，F，C，E共线，∠B＝∠E，BF＝EC，添加一个条件，不能判断△ABC≌△DEF的是（ ）
A．AB＝DEB．∠A＝∠DC．AC＝DFD．AC∥FD
3．如图，AD是△ABC的角平分线，DF⊥AB于点F，且DE＝DG，S△ADG＝24，S△AED＝18，则△DEF的面积为（ ）
A．2B．3C．4D．6
4．如图，若△ABC≌△ADE，则下列结论中一定成立的是（ ）
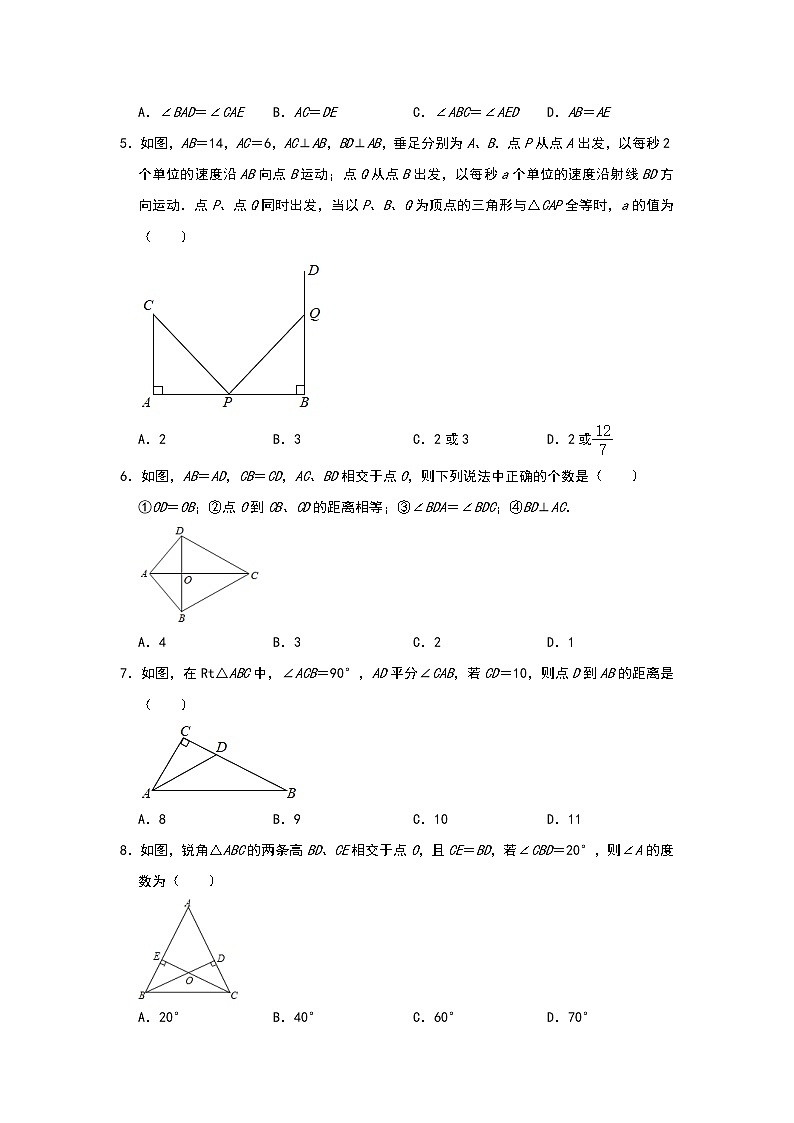
A．∠BAD＝∠CAEB．AC＝DEC．∠ABC＝∠AEDD．AB＝AE
5．如图，AB＝14，AC＝6，AC⊥AB，BD⊥AB，垂足分别为A、B．点P从点A出发，以每秒2个单位的速度沿AB向点B运动；点Q从点B出发，以每秒a个单位的速度沿射线BD方向运动．点P、点Q同时出发，当以P、B、Q为顶点的三角形与△CAP全等时，a的值为（ ）
A．2B．3C．2或3D．2或
6．如图，AB＝AD，CB＝CD，AC、BD相交于点O，则下列说法中正确的个数是（ ）
①OD＝OB；②点O到CB、CD的距离相等；③∠BDA＝∠BDC；④BD⊥AC．
A．4B．3C．2D．1
7．如图，在Rt△ABC中，∠ACB＝90°，AD平分∠CAB，若CD＝10，则点D到AB的距离是（ ）
A．8B．9C．10D．11
8．如图，锐角△ABC的两条高BD、CE相交于点O，且CE＝BD，若∠CBD＝20°，则∠A的度数为（ ）
A．20°B．40°C．60°D．70°
9．公元前6世纪，古希腊哲学家泰勒斯这样测得轮船到海岸的距离：如图所示，在海边灯塔上进行测量，直立一根可以原地转动的竖竿EF（垂直于地面），在其上一点A处连接一个可以绕A转动并固定在任意位置上的横杆，先转动横杆使其转向船的位置B，再转动竖竿EF，使横杆对准岸上的某一点C，然后测量D、C的距离，即得D、B的距离，哲学家得到△ADC≌△ADB的依据是（ ）
A．SSSB．SASC．ASAD．HL
10．如图，AB＝AD，AC＝AE，∠DAB＝∠CAE＝50°，以下四个结论：①△ADC≌△ABE；②CD＝BE；③∠DOB＝50°；④点A在∠DOE的平分线上，其中结论正确的个数是（ ）
A．1B．2C．3D．4
二．填空题（每小题3分，共21分）
11．如图，∠BCA＝∠DAC，请你添加一个条件： ，可得△ACB≌△CAD．
12．如图，若AB，CD相交于点E，若△ABC≌△ADE，且点B与点D对应，点C与点E对应，∠BAC＝28°，则∠B的度数是 °．
13．如图，∠C＝90°，∠A＝30°，BD为角平分线，则S△ABD：S△CBD＝ ．
14．如图，在△ABC中，∠B＝∠C，BF＝CD，BD＝CE，若∠A＝40°，则∠FDE＝ ．
15．如图，A，B两点分别位于一个池塘的两端，小亮想用绳子测量A，B间的距离，但绳子不够长，聪明的小亮想出一个办法：先在地上取一个可以直接到达B点的点C，连接BC，取BC的中点P（点P可以直接到达A点），利用工具过点C作CD∥AB交AP的延长线于点D，此时测得CD＝200米，那么A，B间的距离是 米．
16．在Rt△ABC中，∠BAC＝90°，AB＝AC＝1，以AC为腰在Rt△ABC外部找一个点作等腰Rt△ACD，则线段BD的长为 ．
17．如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，得到下列四个结论：①AD和EF互相垂直平分；②AE＝AF；③当∠BAC＝90°时，AD＝EF；④DE是AB的垂直平分线．其中正确的是 （填序号）．
三．解答题（共49分）
18．如图，在△ABC中，AB＝AC，AD⊥BC于点D，BE⊥AC于点E，AD、BE相交于点H，AE＝BE．试说明：
（1）△AEH≌△BEC．
（2）AH＝2BD．
19．如图，∠A＝∠B，AE＝BE，点D在AC边上，∠1＝∠2，AE，BD相交于点O．
（1）求证：△AEC≌△BED；
（2）若∠C＝70°，求∠AEB的度数．
20．如图，已知EC＝AC，∠BCE＝∠ACD，∠A＝∠E，BC＝3．求DC的值．
21．如图，AB＝AC，直线l过点A，BM⊥直线l，CN⊥直线l，垂足分别为M、N，且BM＝AN．
（1）求证△AMB≌△CNA；
（2）求证∠BAC＝90°．
22．如图，有一池塘，要测池塘两端A、B的距离，可先在平地上取一个点C，从点C不经过池塘可以直接到达点A和B，连接AC并延长到点D，使CD＝CA，连接BC并延长到点E，使CE＝CB，连接DE，那么量出DE的长就是A、B的距离，为什么？请结合解题过程，完成本题的证明．
证明：在△DEC和△ABC中，
，
∴△DEC≌△ABC（SAS），
∴ ．
23．（1）阅读理解：如图1，在△ABC中，若AB＝10，BC＝8．求AC边上的中线BD的取值范围，小聪同学是这样思考的：延长BD至E，使DE＝BD，连接CE．利用全等将边AB转化到CE，在△BCE中利用三角形三边关系即可求出中线BD的取值范围，在这个过程中小聪同学证三角形全等用到的判定方法是 ；中线BD的取值范围是 ．
（2）问题拓展：如图2，在△ABC中，点D是AC的中点，分别以AB，BC为直角边向△ABC外作等腰直角三角形ABM和等腰直角三角形BCN，其中∠ABM＝NBC＝∠90°，连接MN，探索BD与MN的关系，并说明理由．